lógica equivalente -anos

FACULDADE DE TECNOLOGIA SENAC PELOTAS
Curso Superior de Tecnologia em Análise e Desenvolvimento de Sistemas
Matemática Aplicada – Edécio Fernando Iepsen
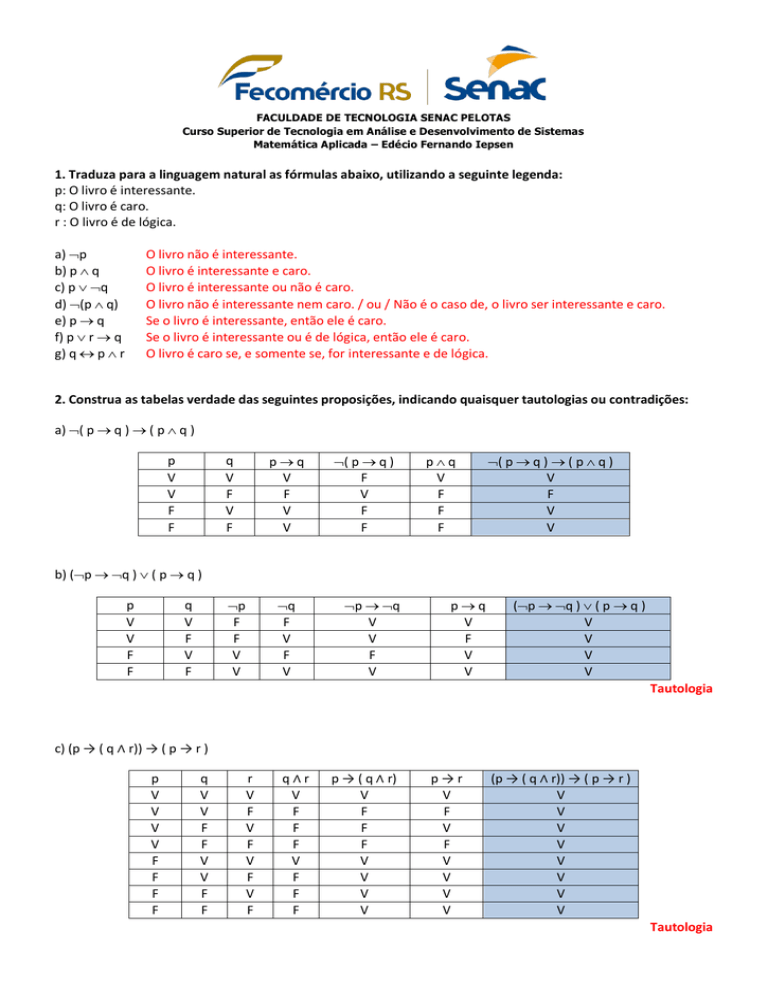
1. Traduza para a linguagem natural as fórmulas abaixo, utilizando a seguinte legenda:
p: O livro é interessante.
q: O livro é caro.
r : O livro é de lógica.
a) p
b) p  q
c) p  q
d) (p  q)
e) p  q
f) p  r  q
g) q  p  r
O livro não é interessante.
O livro é interessante e caro.
O livro é interessante ou não é caro.
O livro não é interessante nem caro. / ou / Não é o caso de, o livro ser interessante e caro.
Se o livro é interessante, então ele é caro.
Se o livro é interessante ou é de lógica, então ele é caro.
O livro é caro se, e somente se, for interessante e de lógica.
2. Construa as tabelas verdade das seguintes proposições, indicando quaisquer tautologias ou contradições:
a) ( p  q )  ( p  q )
p
V
V
F
F
pq
V
F
V
V
q
V
F
V
F
( p  q )
F
V
F
F
pq
V
F
F
F
( p  q )  ( p  q )
V
F
V
V
b) (p  q )  ( p  q )
p
V
V
F
F
p
F
F
V
V
q
V
F
V
F
q
F
V
F
V
p  q
V
V
F
V
pq
V
F
V
V
(p  q )  ( p  q )
V
V
V
V
Tautologia
c) (p → ( q ∧ r)) → ( p → r )
p
V
V
V
V
F
F
F
F
q
V
V
F
F
V
V
F
F
r
V
F
V
F
V
F
V
F
q∧r
V
F
F
F
V
F
F
F
p → ( q ∧ r)
V
F
F
F
V
V
V
V
p→r
V
F
V
F
V
V
V
V
(p → ( q ∧ r)) → ( p → r )
V
V
V
V
V
V
V
V
Tautologia
d) ( p → q ) → (( p ∨ r ) ↔ ( q ∧ r ))
p
V
V
V
V
F
F
F
F
q
V
V
F
F
V
V
F
F
p∨r
V
V
V
V
V
F
V
F
r
V
F
V
F
V
F
V
F
q∧r
V
F
F
F
V
F
F
F
(( p ∨ r ) ↔ ( q ∧ r ))
V
F
F
F
V
V
F
V
p→q
V
V
F
F
V
V
V
V
( p → q ) → (( p ∨ r ) ↔ ( q ∧ r ))
V
F
V
V
V
V
F
V
3. Verifique, a partir da construção de tabelas verdade, se as proposições abaixo são equivalentes:
a) (p  q )  p  q
p
V
V
F
F
q
V
F
V
F
q
F
V
F
V
p  q
F
V
F
F
(p  q )
V
F
V
V
p
V
V
F
F

pq
V
F
V
V
Q
V
F
V
F
São Equivalentes
b) ( p → q ) ∨ r ⇔ ( p ∧ r ) → q
p
V
V
V
V
F
F
F
F
q
V
V
F
F
V
V
F
F
r
V
F
V
F
V
F
V
F
p→q
V
V
F
F
V
V
V
V
(p→q)∨r
V
V
V
F
V
V
V
V
⇔
p
V
V
V
V
F
F
F
F
q
V
V
F
F
V
V
F
F
r
V
F
V
F
V
F
V
F
r
F
V
F
V
F
V
F
V
p ∧ r
F
V
F
V
F
F
F
F
q
F
F
V
V
F
F
V
V
( p ∧ r ) → q
V
F
V
V
V
V
V
V
Não São Equivalentes
4. Marque a resposta correta:
1. Se o sino da igreja toca e minha avó o escuta, então minha avó vai para a igreja. Uma afirmação equivalente a
essa, do ponto de vista lógico, é:
A ( ) Se minha avó não o escuta, então o sino da igreja não toca e minha avó não vai para a igreja.
B ( ) Minha avó não o escuta ou o sino da igreja toca ou minha avó vai para a igreja.
C ( ) Se o sino da igreja toca e minha avó vai para a igreja, então minha avó o escuta.
D ( x ) Se minha avó não vai para a igreja, então o sino da igreja não toca ou minha avó não o escuta.
E ( ) Se o sino da igreja não toca ou minha avó não o escuta, então minha avó não vai para a igreja.
2. Vou à academia todos os dias da semana e corro três dias na semana. Uma afirmação que corresponde à
negação lógica da afirmação anterior é
A ( x ) Não vou à academia todos os dias da semana ou não corro três dias na semana.
B ( ) Vou à academia quase todos os dias da semana e corro dois dias na semana.
C ( ) Nunca vou à academia durante a semana e nunca corro durante a semana.
D ( ) Não vou à academia todos os dias da semana e não corro três dias na semana.
E ( ) Se vou todos os dias à academia, então corro três dias na semana.
3. Um enunciado é uma tautologia quando não puder ser falso, um exemplo é:
A ( ) Está fazendo sol e não está fazendo sol.
B ( ) Está fazendo sol.
C ( ) Se está fazendo sol, então não está fazendo sol.
D ( ) Não está fazendo sol.
E ( x ) Está fazendo sol ou não está fazendo sol.
4. Considerem-se as proposições P, Q e R e a seguinte linha de uma tabela-verdade, em que V representa o valor
lógico verdadeiro, F, o falso.
Os valores lógicos que substituem corretamente as letras X e Y, respectivamente, são:
A ( ) V e F.
B ( ) V e V.
C ( ) F e V.
D ( x ) F e F.
5. A proposição ~ ( p ∨ q ) é equivalente a
A ( ) ~ p ∨ ~ q.
B ( ) ~ p ∨ q.
C ( ) ~ p ∧ q.
D ( ) p ∧ q.
E ( x ) ~ p ∧ ~ q.
6. Sejam as proposições:
p: O rato entrou no buraco.
q: O gato seguiu o rato.
Assinale a proposição “O rato não entrou no buraco e o gato seguiu o rato” correspondente na linguagem da
lógica.
A ( ) p ^ q.
B ( ) ~ (p ^ q).
C ( ) p ^ ~ q.
D ( x ) ~ p ^ q.
E ( ) ~ p v ~ q.
7. Considere-se a seguinte tabela-verdade, em que V representa o valor lógico verdadeiro e F, o valor lógico falso.
Completando-se corretamente a quarta coluna com os valores lógicos V ou F, e escolhendo-se ao acaso um valor
lógico dessa coluna, a probabilidade de ele ser verdadeiro é de:
A ( ) 37,5%
B ( x ) 50,0%
C ( ) 62,5%
D ( ) 75,0%
8. Qual é a negação de “Todos os alunos gostam de matemática”?
A ( ) Nenhum aluno gosta de matemática.
B ( ) Existem alunos que gostam de matemática.
C ( x ) Existem alunos que não gostam de matemática.
D ( ) Pelo menos um aluno gosta de matemática.
E ( ) Apenas um aluno não gosta de matemática.
9. A negação de “Se a canoa não virar, eu chego lá” é:
A ( x ) A canoa não vira e eu não chego lá.
B ( ) Se a canoa virar, eu não chego lá.
C ( ) Se a canoa não virar, eu não chego lá.
D ( ) A canoa vira e eu chego lá.
E ( ) Se eu não chego lá, a canoa vira.
10. Em uma empresa, o gerente afixou o seguinte informe no quadro de avisos: “Se um funcionário não faltar em
determinado mês, ganhará um bônus de 100 reais". Pode-se concluir corretamente que, em determinado mês:
A ( x ) se um funcionário não ganhou um bônus de 100 reais, então ele faltou
B ( ) se um funcionário não ganhou um bônus de 100 reais, então ele não faltou
C ( ) se um funcionário ganhou um bônus de 100 reais, então ele faltou
D ( ) se um funcionário ganhou um bônus de 100 reais, então ele não faltou
11. Sejam as proposições, p: Marta é inteligente e q: Raquel não joga tênis. Então, ~(~p v q) em linguagem
corrente, é:
A ( ) Marta é inteligente ou Raquel não joga tênis.
B ( x ) Marta é inteligente e Raquel joga tênis.
C ( ) Marta não é inteligente e Raquel não joga tênis.
D ( ) Marta não é inteligente ou Raquel joga tênis.
E ( ) Marta é inteligente ou Raquel joga tênis.
12. Renato falou a verdade quando disse:
- Corro ou faço ginástica.
- Acordo cedo ou não corro.
- Como pouco ou não faço ginástica.
Certo dia, Renato comeu muito.
É correto concluir que, nesse dia, Renato:
A ( ) correu e fez ginástica;
B ( ) não fez ginástica e não correu;
C ( ) correu e não acordou cedo;
D ( x ) acordou cedo e correu;
E ( ) não fez ginástica e não acordou cedo.
13. Se Aldo se casa com Bianca, então Bianca fica feliz. Se Bianca fica feliz, então Clara chora. Se Clara chora,
então Dione consola Clara. Ora, Dione não consola Clara, logo:
A ( ) Clara não chora e Bianca fica feliz.
B ( x ) Clara não chora e Aldo não se casa com Bianca.
C ( ) Bianca não fica feliz e Aldo se casa com Bianca.
D ( ) Bianca fica feliz e Aldo se casa com Bianca.
E ( ) Clara chora e Bianca fica feliz.
5. Use lógica proposicional para provar a validade dos seguintes argumentos:
1. Se estudo, passo no concurso. Se não estudo, trabalho. Logo, se não passo no concurso, trabalho.
E = Estudo
P = Passo no concurso
T = Trabalho
Fórmula: (E  P) ^ (E  T)  (P  T)
1.
2.
3.
4.
5.
6.
EP
E  T
P
.:. T
E
T
hip
hip
hip
conc
1,3 mt
2,5 mp
2. Se Paulo é um bom nadador, então ele é um bom corredor. Se Paulo é um bom corredor, então ele é um bom
ciclista. Portanto, se Paulo é um bom nadador, então ele é um bom ciclista.
N = Paulo é um bom Nadador
C = Paulo é um bom Corredor
I = Paulo é um bom ciclista
Fórmula: (N  C) ^ (C  I)  (N  I)
1.
2.
3.
4.
5.
6.
NC
CI
N
.:. I
NI
I
hip
hip
hip
conc
1,2 sh
5,3 mp
3. Se navegar é preciso, então viver não é preciso. Se navegar não é preciso, então criar não é preciso. Mas criar é
preciso, portanto viver não é preciso.
N = Navegar é preciso
V = Viver é preciso
C = Criar é preciso
Fórmula: (N  V) ^ (N  C) ^ (C  V)
1.
2.
3.
4.
5.
6.
7.
N  V
N  C
C
.:. V
N
N
V
hip
hip
hip
conc
2,3 mt
5 dn
1,6 mp
4. Se Jane é a mais popular, ela será eleita. Se Jane é a mais popular, então Carlos vai renunciar. Portanto, se Jane
é a mais popular, ela será eleita e Carlos renunciará.
P : Jane é a mais popular
E : Jane será eleita
C : Carlos vai renunciar
Fórmula: (P  E) ^ (P  C)  (P  (E ^ C))
1.
2.
3.
4.
5.
6.
7.
PE
PC
P
.:. E ^ C
E
C
E^C
hip
hip
hip
conc
1,3 mp
2,3 mp
5,6 conj
5. Se o programa possui erros de sintaxe, sua compilação produz mensagem de erro. Se o programa não possui
erros de sintaxe, sua compilação produz um executável. Se tivermos um programa executável, podemos executálo para obter um resultado. Não temos como executar o programa para obter um resultado. Logo, a compilação
do programa produz uma mensagem de erro.
S : Programa possui erros de Sintaxe
M : A compilação do programa produz Mensagens de erro
E : A compilação do programa produz um Executável
R : Pode-se executar o programa para obter um Resultado
Fórmula: (S  M) ^ (S  E) ^ (E  R) ^ R  M
1.
2.
3.
4.
5.
6.
7.
8.
9.
SM
S  E
ER
R
.:. M
E
S
S
M
hip
hip
hip
hip
conc
3,4 mt
2,6 mt
7 dn
1,8 mp
Extra:
Se meu cliente fosse culpado, a faca estaria na gaveta. Ou a faca não estava na gaveta ou Jason viu a faca. Se a
faca não estava lá no dia 10 de outubro, então Jason não viu a faca. Além disso, se a faca estava lá no dia 10 de
outubro, então a faca estava na gaveta e o martelo estava no celeiro. Mas todos sabemos que o martelo não
estava no celeiro. Portanto, senhoras e senhores, meu cliente é inocente.