Teorema do Impulso com ângulo

Teorema do Impulso com ângulo
1. (Pucpr 2015) A figura a seguir ilustra uma visão superior de uma mesa de sinuca, onde uma
bola de massa 400 g atinge a tabela com um ângulo de 60 com a normal e ricocheteia
formando o mesmo ângulo com a normal. A velocidade da bola, de 9 m / s, 9 m/s, altera apenas
a direção do movimento durante o choque, que tem uma duração de 10 ms.
A partir da situação descrita acima, a bola exerce uma força média na tabela da mesa de:
a) 360 N.
b) 5400 N.
c) 3600 N.
d) 4000 N.
e) 600 N.
2. (Unesp 2015) O gol da conquista do tetracampeonato pela Alemanha na Copa do Mundo de
2014 foi feito pelo jogador Götze. Nessa jogada, ele recebeu um cruzamento, matou a bola no
peito, amortecendo-a, e chutou de esquerda para fazer o gol. Considere que, imediatamente
antes de tocar o jogador, a bola tinha velocidade de módulo V1  8 m / s em uma direção
perpendicular ao seu peito e que, imediatamente depois de tocar o jogador, sua velocidade
manteve-se perpendicular ao peito do jogador, porém com módulo V2  0,6 m / s e em sentido
contrário.
www.nsaulasparticulares.com.br
Página 1 de 7
Admita que, nessa jogada, a bola ficou em contato com o peito do jogador por 0,2 s e que,
nesse intervalo de tempo, a intensidade da força resultante (FR ), que atuou sobre ela, variou
em função do tempo, conforme o gráfico.
Considerando a massa da bola igual a 0,4 kg, é correto afirmar que, nessa jogada, o módulo
da força resultante máxima que atuou sobre a bola, indicada no gráfico por Fmáx , é igual, em
newtons, a
a) 68,8.
b) 34,4.
c) 59,2.
d) 26,4.
e) 88,8.
3. (Ufrn 2012) O funcionamento de um gerador eólico é baseado na interação entre suas pás e
o vento. Nessa interação, as pás do gerador funcionam como defletor para a massa de ar
incidente. Durante a interação, o vetor quantidade de movimento do ar incidente Qinicial , tem a
orientação alterada para quantidade de movimento do ar refletido, Qfinal , pela presença das
pás, conforme mostrado na figura abaixo.
A variação da quantidade de movimento da massa de ar incidente sobre as pás faz com que
elas girem em torno de seu eixo gerando energia elétrica. Tal variação na quantidade de
movimento do ar, ΔQ, é expressa por ΔQ  Qfinal  Qinicial.
Neste sentido, a composição de vetores que melhor representa a variação da quantidade do
movimento do ar está representada por:
www.nsaulasparticulares.com.br
Página 2 de 7
a)
b)
c)
d)
4. (Uftm 2012) Num trecho plano e horizontal de uma estrada, um carro faz uma curva
mantendo constante o módulo da sua velocidade em 25 m/s. A figura mostra o carro em duas
posições, movendo-se em direções que fazem, entre si, um ângulo de 120°.
Considerando a massa do carro igual a 1 000 kg, pode-se afirmar que, entre as duas posições
indicadas, o módulo da variação da quantidade de movimento do veículo, em (kg  m)/s, é igual
a
www.nsaulasparticulares.com.br
Página 3 de 7
a) 10 000.
b) 12 500.
c) 25 000.
d) 12 500 2.
e) 25 000 2.
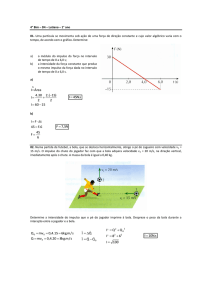
5. (Ufg 2001) Em época de férias escolares, é comum ver pessoas empinando papagaio. O
papagaio em voo, preso à mão de uma pessoa por uma linha ideal, ao interagir com o vento,
desvia uma massa de ar na razão de 0,30kg/s. Considere a situação mostrada na figura, na
qual o vento incide horizontalmente sobre o papagaio e é defletido verticalmente para baixo.
Os módulos das velocidades dos ventos incidente e defletido são iguais a 6,0m/s. Dessa forma,
( ) ( ) com o papagaio em equilíbrio a uma determinada altura, a componente vertical da
força do vento sobre ele tem o mesmo módulo, a mesma direção e sentido oposto ao seu
peso.
( ) ( ) em um intervalo de 2,0s, o impulso sobre o papagaio é de, aproximadamente, 5,1Ns.
( ) ( ) a força que o vento exerce no papagaio, enquanto ele estiver parado no ar, tem
módulo de 1,8N.
( ) ( ) para fazer o papagaio subir, a pessoa deverá correr em sentido oposto ao do vento.
Nesse caso, o módulo da velocidade do vento defletido diminuirá.
www.nsaulasparticulares.com.br
Página 4 de 7
Gabarito:
Resposta da questão 1:
[A]
Para a resolução da questão usaremos o teorema do Impulso
I  ΔQ (1)
Onde,
I  impulso da força média em N/s;
ΔQ  variação da quantidade de movimento em kg m/s que é calculada vetorialmente, como
vemos nas figuras:
ΔQ  Qf  Qi (2)
Nota-se que o triangulo formado é equilátero, pois todos os ângulos internos são iguais entre
si, sendo assim, a variação da quantidade de movimento ΔQ é exatamente igual à quantidade
de movimento inicial Qi e final Qf , isto é, em módulo
m
m
ΔQ  Qi  m  v  0,4kg  9  3,6kg
s
s
Sabendo que o módulo do Impulso é dado por:
I  Fm  t (3)
Juntando as equações (3) e (1), temos:
Fm  t  ΔQ (4)
Donde sai a força média da colisão da bola com a tabela, em módulo:
ΔQ
3,6Ns
Fm 

 360N
t
10  103 s
www.nsaulasparticulares.com.br
Página 5 de 7
Resposta da questão 2:
[B]
Orientando a trajetória no sentido da velocidade de chegada, V1  8 m/s e V2   0,6 m/s.
Durante a colisão, o impulso da força resultante é numericamente igual à área entre a linha do
gráfico e o eixo dos tempos. Assim, aplicando o teorema do impulso:
Fmáx Δt
2 m Δv
2  0,4  0,6  8
IF  ΔQ 
 m Δv  Fmáx 


2
Δt
0,2
Fmáx  34,4 N.
Resposta da questão 3:
[C]


ΔQ  Qfinal  Qinicial  ΔQ  Qfinal  Qinicial .
Ou seja, subtrair é somar com o oposto.
Usando a regra da poligonal:
Resposta da questão 4:
[C]
Apesar de a velocidade do veículo não mudar em relação a sua intensidade (25 m/s), devemos
lembrar que a velocidade é uma grandeza vetorial, e, como tal, a mudança do seu sentido e
direção implica na sua variação. Como a quantidade de movimento também é uma grandeza
vetorial definida como o produto da massa de um corpo pela velocidade, a mudança da
velocidade implica na sua variação. Observe as ilustrações:
www.nsaulasparticulares.com.br
Página 6 de 7
Assim, o vetor da variação d quantidade de movimento é dado por:
ΔQ  QF  Q0
Agora que encontramos o vetor da variação da quantidade de movimento, devemos notar que
devido ao ângulo formado entre o vetor Q0 e QF ser de 60° e ainda que | Q0 |=| QF |, o triângulo
formado pelos vetores acima é equilátero. Assim sendo:
| ΔQ |=m.| v 0 | = 1000.25
 ΔQ  25000kg.m / s
Resposta da questão 5:
FVFF
www.nsaulasparticulares.com.br
Página 7 de 7