aula 7 e 8 - GEOCITIES.ws

Aulas 07 e 08
Área do retângulo
Comumente chamamos um dos lados de um retângulo de
comprimento (ou base) e o outro de largura (ou altura). Indicamos por: b =
medida do comprimento (ou da base). h = medida da largura (ou da altura).
b
Assim temos:
Área do retângulo = b . h
h
A =b.h
A=b.h
h
b
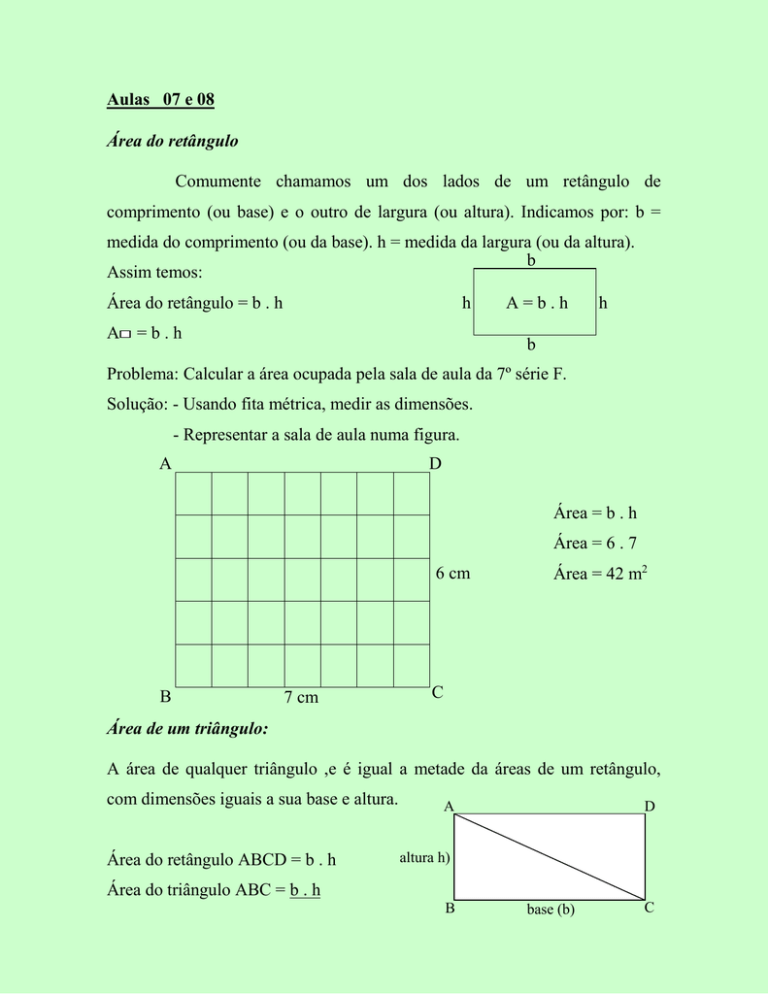
Problema: Calcular a área ocupada pela sala de aula da 7º série F.
Solução: - Usando fita métrica, medir as dimensões.
- Representar a sala de aula numa figura.
A
D
Área = b . h
Área = 6 . 7
6 cm
B
7 cm
Área = 42 m2
C
Área de um triângulo:
A área de qualquer triângulo ,e é igual a metade da áreas de um retângulo,
com dimensões iguais a sua base e altura.
Área do retângulo ABCD = b . h
A
D
altura h)
Área do triângulo ABC = b . h
B
base (b)
C
2
Área do triângulo ACD = b . h
2
Podemos considerar qualquer lado do triângulo como base. A altura a ser
considerada é uma perpendicular relativa a esse lado.
Problema: Sabendo que as dimensões da sala de aula da 7ª série F são 7m de
comprimento e 6m de largura. Formando um retângulo ABCD. Se
traçarmos um diagonal do ponto A ao ponto C, teríamos 2
triângulos. Qual será a área ocupada por cada um dos triângulos.
A
D
Área do retângulo ABCD = b . h
Área do retângulo ABCD = 7 . 6
Área do retângulo ABCD = 42m2
6 cm Área do triângulo ABC = b . h
2
Área do triângulo ABC = 7 . 6
2
Área do triângulo ABC = 21 m2
B
C
7 cm
Área do triângulo ACD = 21 m2
Área do círculo
Se P é um ponto de um plano e r um número positivo, o conjunto de todos os
pontos do plano cuja distância a P é igual a r é a circunferência de centro P e
raio r.
r
P
Mas o conjunto de todos os pontos do plano cuja distância a P é menor ou
igual a r já não é mais uma circunferência, e sim um círculo de centro P e raio
r.
r
P
Podemos imaginar um círculo como sendo formado por infinitas
circunferências de raios cada vez menores.
“Esticando” cada uma das circunferências, estamos decompondo o círculo e
transformando-o em um triângulo em que a base é a maior circunferência
retificada.
 . 2r
As demais circunferências retificadas vão compondo a superfície de um
triângulo retângulo com altura igual ao raio r.
r
 . 2r
Intuitivamente, podemos observar que a área do círculo é igual a área desse
triângulo:
Área do círculo = área do triângulo
= base . altura
2
= 2r .  . r
2
=  . r2
A área do círculo de 9 cm de raio é aproximadamente igual a:

 . r2 = 3,14
. 92

. 81
= 3,14

= 234,54
cm2
ou

= 2,34 m2