TP3

3ª AULA “PRÁTICA” DE FÍSICA MÉDICA
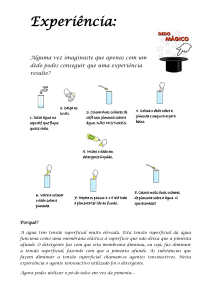
Aplicação do formalismo da tensão superficial ao funcionamento dos pulmões
I. Se juntar dois balões iguais, um mais cheio de ar do que o outro, o que acontecerá?
Explique esse mecanismo.
II. Explique, detalhadamente, por que razão os recém-nascidos prematuros têm, em
geral, problemas respiratórios.
3. Tensão superficial e capilaridade
Como se sabe, as moléculas constituintes de um líquido interactuam através de
forças atractivas que as mantêm num estado condensado, forças de coesão. Numa
molécula que se encontre no interior de um líquido, a soma dessas forças, uma vez que
se encontram igualmente distribuídas em todas as direcções, é nula. No entanto, o
mesmo já não acontece com as moléculas que se encontram na superfície do líquido.
Essas moléculas não sofrem influência de moléculas acima delas e, portanto, a força
resultante que lhes está aplicada tem o sentido do exterior para o interior do líquido1.
Essa força resulta numa contracção da superfície do líquido a qual passa a comportar-se
como uma membrana sob uma certa tensão. Esta situação pode ser descrita por uma
força tangencial à superfície do líquido. Deste formalismo resulta a grandeza tensão
superficial, que é descrita do seguinte modo: considere-se um segmento de recta, l,
numa dada direcção sobre a superfície livre do líquido e F a força mínima perpendicular
a esse segmento que é necessário aplicar-lhe para que a área da superfície do líquido
sofra deformação, a tensão superficial será, então, dada pela razão:

F
l
equação 3.1
Um outro fenómeno resultante das forças de coesão nos líquidos e observável
nos pontos em que a superfície livre do líquido toca no recipiente que o contém é o de
capilaridade. Na verdade, as moléculas que se encontram na vizinhança das paredes do
recipiente sofrem forças de atracção das moléculas constituintes do recipiente, forças de
aderência. E neste caso duas situações poderão ocorrer: ou as forças de aderência são
superiores à força de coesão do líquido e, então, o líquido tende a subir pelas paredes do
recipiente (ver figura 3.1 a) ), ou as forças de aderência são menores do que as de coesão
e a superfície livre do líquido tende a curvar para o interior do mesmo (ver figura 3.1
b) ).
Figura 3.1 - Representação do comportamento dos líquidos em contacto com um recipiente, devido
às forças de aderência. (Adap. de P. Davidovits, 2001).
1
Em rigor, as moléculas pertencentes ao líquido, mas que se encontram na superfície deste, sofrem
influência de moléculas acima delas constituintes do gás sob o qual o líquido se encontra. No entanto,
como as forças de coesão entre as moléculas do gás e as moléculas do líquido são muito diferentes e,
portanto, o resultado continua válido.
1
O contacto entre o líquido e as paredes do recipiente é, pois, caracterizado pelo
ângulo representado na figura 3.1 que é dependente da natureza do líquido e do material
do recipiente. Na tabela 3.1 pode-se observar diversos ângulos de contacto, para
diferentes pares de interfaces.
Interfaces
Água -vidro (limpo)
Álcool etílico-vidro (limpo)
Mercúrio-vidro
Água-prata
Água-parafina
Ângulo de contacto
0º
0º
140º
90º
107º
Tabela 3.1 -Ângulo de contacto de diversas interfaces líquido-sólido. (Adap. de P. Davidovits, 2001).
O fenómeno da capilaridade é particularmente notório quando se introduz um
tubo muito fino no interior de um líquido. Nessa situação é possível observar-se a
subida do líquido no interior do tubo (ver figura 3.2 a) ) ou a sua descida (ver figura 3.2
b) ).
Figura 3.2 - Ilustração do fenómeno de capilaridade. (Adap. de P. Davidovits, 2001).
Em seguida, calcular-se-á a variação da altura do líquido em função da tensão
superficial, T; do raio do tubo, R; da densidade do líquido, ρ; do ângulo de contacto, θ; e
da aceleração da gravidade.
O peso da coluna de líquido é:
P  mg  Vg  gR 2 h .
A força máxima associada à tensão superficial em redor da coluna de líquido
será, tendo em conta o que anteriormente foi dito:
Fm  2RT .
Ora a componente da força superficial que compensa o peso é a vertical, ou seja,
será o produto: Fm cos  e, portanto, visto que o líquido se encontra em equilíbrio é
válida a igualdade:
Fm cos   gR 2 h  2RT cos   gR 2 h  h 
2T cos 
.
gR
Uma outra consequência interessante da tensão superficial é o facto de tanto as
bolhas, como as gotas terem um formato esférico. Para compreender este efeito,
comece-se por referir que o valor da tensão superficial pode ser interpretado como uma
energia por unidade de área2. Aplicando o critério de energia mínima, facilmente se
2
Para entender esta equivalência basta fazer uma análise dimensional: a tensão superficial tem unidade
N m-1, que é equivalente a N m m-2, ou seja, J m-2 que corresponde, efectivamente, a uma unidade de
2
compreende que, para um determinado líquido (o que corresponde a uma dada tensão
superficial), a geometria que minimiza a energia é aquela que corresponde à menor área.
E, como é sabido, a esfera é o sólido geométrico que menor área superficial tem, para
um dado volume considerado.
Relacionada com este aspecto está a Lei de Laplace que estabelece a relação
entre as diferenças de pressão no interior, Pi, e no exterior, Po, de uma gota; o seu raio, r,
e a tensão superficial do líquido de que é formada, σ:
Pi  Po 
2
.
r
equação 3.2
Note-se que esta diferença de pressão é dependente do sistema. Por exemplo, ao
analisar-se o que se passa com uma bolha3 a diferença de pressão no interior e no
exterior da bolha é duas vezes superior, vindo dada por:
Pi  Po 
4
.
r
equação 3.3
Ambas as expressões resultam em duas conclusões extremamente interessantes:
o primeiro é o facto de a pressão no interior de uma gota (o mesmo é válido para uma
bolha) ser maior no interior do que no exterior da mesma; o segundo refere que, para a
mesma tensão superficial, quanto maior for o raio, menor será a pressão no interior da
gota (ou bolha). Embora com ligeiras adaptações4, é este o motivo pelo qual se
colocarmos em contacto dois balões semelhantes, um deles menos cheio do que o outro,
verifica-se que o balão menos cheio se esvazia, aumentando o raio do outro (a pressão
no interior do balão de maior raio é menor do que a pressão no interior do balão de
menor raio).
3.1 Funcionamento dos pulmões e tensão superficial
Se atendermos à anatomia pulmonar, recordamos que a troca de gás entre os
pulmões e os vasos sanguíneos ocorre ao nível dos alvéolos, que são pequenos sacos
cujos raios são, em média, de 60 μm. Se o mecanismo descrito no final da secção
anterior fosse aplicável aos alvéolos, facilmente se compreenderia que a respiração era
impossível, uma vez que o ar dos alvéolos de menor raio transferir-se-ia para os
alvéolos de maior raio, criando uma situação limite em que alguns alvéolos rebentariam
e outros colapsariam. Ora esta situação não se observa porque, a cobrir as paredes
internas dos alvéolos, se encontra um líquido contendo lipoproteínas5 que alteram as
propriedades elásticas da membrana. De facto, verifica-se que, por acção dessas
proteínas, quanto menor for o raio dos alvéolos, menor será a sua tensão superficial,
pelo que a tendência para, nestas condições, a pressão interior aumentar, é compensada
com o aumento da elasticidade e, portanto, os alvéolos menores não chegam a perder o
seu gás interior.
energia por área.
3
Uma bolha, ao contrário de uma gota, é formada por uma fina camada de líquido, devendo considerar-se
duas superfícies (a interior e a exterior), e, portanto, os efeitos da tensão superficial são duplicados.
4
Deve ter-se em atenção que num balão a tensão superficial se altera com o raio, enquanto que numa
bolha a tensão superficial se mantém constante (o aumento de raio numa bolha é conseguido à custa da
diminuição de espessura da película de líquido de que é feita). No entanto, a variação da tensão superficial
num balão não é suficiente para que a maior parte dos resultados válidos para uma bolha não o sejam
também para um balão.
5
A este líquido dá-se o nome de surfactante, uma vez que, tal como outros agentes com o mesmo nome,
quando adicionado a algumas substâncias diminui-lhes a tensão superficial.
3
O mesmo mecanismo explica como é possível, durante a respiração, a entrada e
a saída de ar dos pulmões. Durante a exalação a pressão interior dos alvéolos diminui.
Por outro lado, devido à contracção muscular os alvéolos tendem a diminuir o seu raio.
Ora, nestas condições, se a tensão superficial da membrana dos alvéolos se mantivesse
constante, estes tenderiam a colapsar, uma vez que a diferença de pressão não seria
contrabalançada. O mecanismo contrário observar-se-ia durante a inalação, ou seja, a
pressão no interior dos alvéolos aumentaria e devido à descontracção muscular o seu
raio tenderia a aumentar, rebentando os alvéolos. Esta tendência só é contrariada, uma
vez mais, devido à presença do agente surfactante que promove o aumento da
elasticidade (diminuição da tensão superficial) para menores raios.
Este mecanismo, explica, pois, a extraordinária importância das concentrações
de surfactante nos alvéolos. Aliás, uma das causas de morte de recém-nascidos,
nomeadamente de bebés prematuros, é precisamente a falta de surfactante nos pulmões,
o que dificulta imenso a sua respiração.
4