Aula 4 Modelos CC e CA para Diodos

Aula 4
Modelos CC e CA para Diodos
1
Prof. AC.Seabra-PSI/EPUSP 2013
1
PSI 2223 – Introdução à Eletrônica
Programação para a Primeira Prova
Prof. AC.Seabra-PSI/EPUSP 2013
2
4ª Aula: Modelos CC e CA para Diodos
Na aula passada você foi desafiado a:
-Explicar porque a lei do diodo real é de difícil utilização para
cálculos rápidos de tensões e correntes em um circuito com
diodos
-Listar os modelos alternativos à equação do diodo para cálculos
rápidos em regime CC
-Realizar análises gráficas de comportamento de circuitos com
diodos reais quando submetidos a variações de parâmetros
-Explicar como construir e determinar os parâmetros dos modelos
linearizados para o diodo real
-Empregar modelos linearizados para determinar correntes e
tensões em circuitos com diodos reais
-Discutir a adequação e escolher o modelo apropriado para
realizar uma análise de circuitos empregando diodos reais
Prof. AC.Seabra-PSI/EPUSP 2013
3
4ª Aula: Modelos CC e CA para Diodos
Ao final desta aula você deverá estar apto a:
-Explicar e utilizar a notação empregada em eletrônica para
diferenciar sinais constantes e sinais variáveis no tempo.
-Diferenciar resistências reais, resistências para modelagem em
CC e resistências para modelagem em CA (incrementais)
-Selecionar modelos CC ou CA para realizar análises em circuitos
com diodos em função do tipo de problema
-Calcular resistências e outros parâmetros para modelagem CC e
para modelagem CA
-Descrever o procedimento para cálculo de grandezas CC e CA em
circuitos com diodos
-Calcular tensões e correntes tanto CC como CA em circuitos com
diodos
Prof. AC.Seabra-PSI/EPUSP 2013
4
Na Aula Passada vimos
a Análise por Modelos Linearizados (CC)
O Modelo com VD0 e rD
O Modelo só com VD
Assumimos VD =0,7V
Prof. AC.Seabra-PSI/EPUSP 2013
5
Na Aula Passada vimos
a Análise por Modelos Linearizados (CC)
Exemplo 3.4:
Exata
Livro
Ref em 4mA
Modelo só VD
VD
0,762V
0,735V (-4%) 0,752V (-2%) 0,7V (-8%)
ID
4,28mA
4,26mA (-1%) 4,25mA (-1%) 4,3mA (+1%)
Modelo Diodo Ideal (Chave aberta, chave fechada):
VD = 0; ID = 5mA (17%)
Prof. AC.Seabra-PSI/EPUSP 2013
6
Exercício 3.12 Projete o circuito da Figura E3.12 para proporcionar
uma tensão de saída de 2,4 V. Suponha que os diodos disponíveis
tenham 0,7 V de queda com uma corrente de 1 mA e que V =
0,1 V/década de variação na corrente.
Prof. AC.Seabra-PSI/EPUSP 2013
7
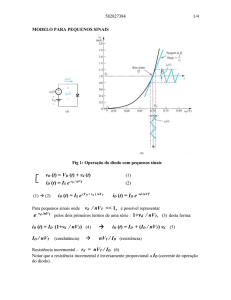
Vamos inserir uma Variação CA na
Entrada (um Pequeno Sinal)
iD
id
Id
iD
ID
Prof. AC.Seabra-PSI/EPUSP 2013
8
Vamos inserir um Pequeno Sinal
na entrada
I(t)
?
t
VDC
Prof. AC.Seabra-PSI/EPUSP 2013
9
Que modelo utilizar para pequenos sinais?
Qual modelo utilizar?
-Modelo chave aberta, chave fechada (diodo ideal)?
-Modelo VD constante = 0,7V?
-Modelo de resistência rD + VD0?
Prof. AC.Seabra-PSI/EPUSP 2013
10
Pequenos sinais (CA)
Tentando utilizar o modelo rD + VD0
-Modelo de resistência rD + VD0
Aprox
ideal
Prof. AC.Seabra-PSI/EPUSP 2013
11
Pequenos sinais (CA)
O ideal é a tangente ao ponto!!!
Muito Melhor
Prof. AC.Seabra-PSI/EPUSP 2013
12
Pequenos sinais (CA)
A tangente ao ponto: uma análise matemática
Qual a tangente à expressão?
I D  I S e VD / nVT
vD (t ) / nVT
i
(
t
)

I
e
v D (t )  VD  vd (t )  D
S
i D (t )  I S e
[VD  vd (t )] / nVT

i D (t )  I S e
VD / nVT
e
vd (t)/ nVT
i D (t )  I D e vd (t)/nVT
Prof. AC.Seabra-PSI/EPUSP 2013
13
Pequenos sinais (CA)
A tangente ao ponto: uma análise matemática
Qual a tangente (primeira derivada) da expressão?
i D (t )  I D e
vd (t)/ nVT

I D vd (t) /nVT
iD (t ) 
e

nVT
vd
Ou podemos representar a expressão de id(t)por uma soma
infinita de termos calculados como as derivadas em um
determinado ponto (Série de Taylor):
vd
onde a  0 e x 
nVT
Prof. AC.Seabra-PSI/EPUSP 2013
14
Pequenos sinais (CA)
A tangente ao ponto: uma análise matemática
i D (t )  I D e vd (t)/nVT
Se
2
3

 1 v




v
v
1
1
d
 I D .1 
  d    d   
6  nVT 

 1 nVT 2  nVT 
vd
 1 podemos fazer uma boa aproximação considerando
nVT
apenas os dois primeiros termos:
i D (t )  I D e
Prof. AC.Seabra-PSI/EPUSP 2013
vd (t)/ nVT
ID
 ID 
v d (t )
nVT
15
Pequenos sinais (CA)
A tangente ao ponto: uma análise matemática
i D (t )  I D e
vd (t)/ nVT
ID
 ID 
v d (t )
nVT
Como iD(t) = ID + id(t), por inspeção:
ID
id (t ) 
v d (t )
nVT
1
rd
nVT
rd 
ID
Prof. AC.Seabra-PSI/EPUSP 2013
16
Exemplo 3.6: Considere o circuito abaixo, alimentado por
uma fonte V+ constituída por um sinal CC de 10V sobre o qual
aplica-se um sinal senoidal de 60Hz com 1Vp de amplitude.
Calcule a tensão CC sobre o diodo e a amplitude do sinal senoidal
sobre ele. Assuma que o diodo tem uma queda de tensão de 0,7V
em 1mA e n=2.
Prof. AC.Seabra-PSI/EPUSP 2013
17
Exemplo 3.6: Considere o circuito abaixo, alimentado por
uma fonte V+ constituída por um sinal CC de 10V sobre o qual
aplica-se um sinal senoidal de 60Hz com 1Vp de amplitude.
Calcule a tensão CC sobre o diodo e a amplitude do sinal senoidal
sobre ele. Assuma que o diodo tem uma queda de tensão de 0,7V
em 1mA e n=2.
Prof. AC.Seabra-PSI/EPUSP 2013
18
Exemplo 3.6: Considere o circuito abaixo, alimentado por
uma fonte V+ constituída por um sinal CC de 10V sobre o qual
aplica-se um sinal senoidal de 60Hz com 1Vp de amplitude.
Calcule a tensão CC sobre o diodo e a amplitude do sinal senoidal
sobre ele. Assuma que o diodo tem uma queda de tensão de 0,7V
em 1mA e n=2.
• 1º : Calcular Ponto Quiescente – Parte CC
• 2º : Calcular Parte Alternada – Parte CA
Prof. AC.Seabra-PSI/EPUSP 2013
19
Exemplo 3.6: Considere o circuito abaixo, alimentado por
uma fonte V+ constituída por um sinal CC de 10V sobre o qual
aplica-se um sinal senoidal de 60Hz com 1Vp de amplitude.
Calcule a tensão CC sobre o diodo e a amplitude do sinal senoidal
sobre ele. Assuma que o diodo tem uma queda de tensão de 0,7V
em 1mA e n=2.
Análise DC
Análise AC
Análise Global: Análise DC + Análise AC
Prof. AC.Seabra-PSI/EPUSP 2013
20
Portanto Exemplo 3.6:
Passos:
- Resolver a parte CC
-Modelo diodo ideal (aberto/fechado)
-Modelo bateria
-Modelo bateria+rD
ID 
(10  0,7)
 0,93mA
10k
- Resolver a parte CA
-Modelo para pequenos sinais
nVT 2  25mV
 53,8
rd 

0,93mA
ID
vd  vs
Prof. AC.Seabra-PSI/EPUSP 2013
rd
54

 5,35mV
R  rd 10k  54
21
Exemplo 3.7: No circuito abaixo temos cerca de 2,1V na saída
(n=2). Queremos saber qual a variação percentual de tensão na
saída quando temos:
(a) 10% de variação na tensão de entrada
(b) Quando acoplamos uma carga na saída (mantendo a tensão
de entrada em 10V fixos)
Sem Carga:
Semcarga:
IR  ID
2,1V
(10  2,1)
1k
 7, 9mA

Prof. AC.Seabra-PSI/EPUSP 2013
22
Exemplo 3.7:
(a) 10% de variação na tensão de entrada
(b) Quando acoplamos uma carga na saída (mantendo a tensão de entrada em 10V fixos)
Sem Carga:
• Parte CC:
• Parte CA:
7, 9mA
VO=2,1V e ID=7,9mA
2,1V
rd 
nVT
2  25mV

 6, 3
ID
7, 9mA
vd  v s
3rd
R  3rd
 1V .
Prof. AC.Seabra-PSI/EPUSP 2013
19
 18, 6mV
1k  19
23
Exemplo 3.7:
(b) Quando acoplamos uma carga na saída (mantendo a tensão de entrada em 10V fixos)
(10  2,1)
 7, 9mA
1k
Com carga: Se I R  cte
Sem carga: I R  I D 
Sem carga: I
R
IR  ID
ID
IL
2,1V
Prof. AC.Seabra-PSI/EPUSP 2013
I D  I R  I L  7, 9m  2,1V 1k  (7, 9  2,1)mA  5, 8mA
Vs  3rd (I D com L  I D sem L )  19.(5, 8  7, 9)  40mV
24