tensão operação -aquecimento

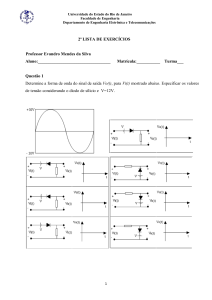
O diodo ideal
Diodos: elemento de circuito não-linear mais simples
e fundamental.
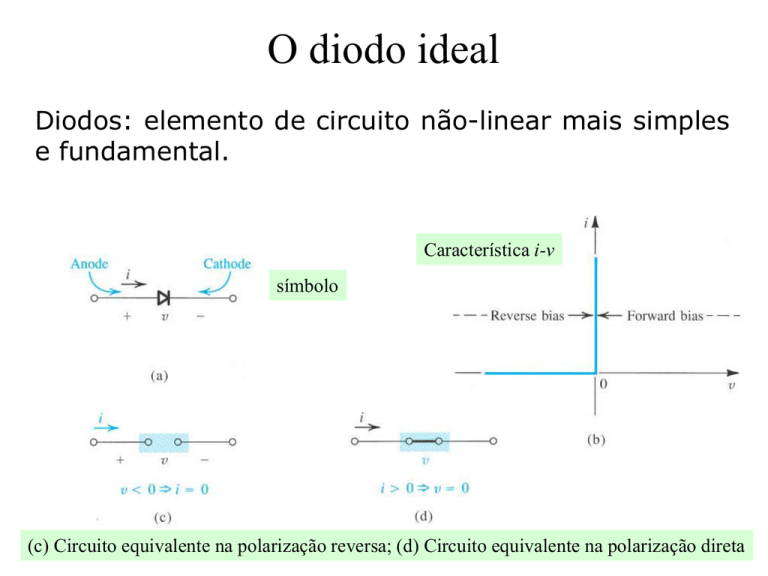
Característica i-v
símbolo
(c) Circuito equivalente na polarização reversa; (d) Circuito equivalente na polarização direta
Modelo equivalente: polarização direta e reversa
Característica i-v: não-linear
Característica i-v ideal: não-linear, mas linear por partes.
Terminal positivo: anodo
Terminal negativo: catodo.
Os dois modos de operação de
diodos ideais e o uso de um circuito
externo para limitar a corrente
direta e a tensão reversa.
Uma aplicação simples: o retificador
Retificador: pode ser utilizado para gerar um sinal
cc a partir de um sinal ca.
(a) Circuito retificador
(b) Valor médio (ou
componente cc) nulo.
(c) Circuito equivalente
quando vI  0.
(e) Valor médio (ou
componente cc) finito
não-nulo.
(d) Circuito equivalente quando vI  0.
Exercícios
Exercício 3.1: Determine a curva característica
transferência vo  vi do circuito da figura anterior item (a).
de
Exercício 3.2: Determine a forma de onda de vD.
Exemplo 3.1: A figura abaixo mostra um circuito para o
carregamento de uma bateria de 12V. Se vs é um sinal senoidal
com 24 V de amplitude máxima, determine a fração de cada
ciclo em que o diodo está conduzindo. A seguir, determine o
valor de pico da corrente do diodo e a tensão reversa máxima
que surge nos terminais do diodo.
Exemplo 3.1
Exemplo de aplicação:
Portas lógicas com diodo
Diodos e resistores podem ser utilizados para implementar
funções lógicas.
Considere um exemplo em lógica positiva:  0V  0 lógico; 
5V  1 lógico. Entradas: vA, vB e vc. Que função lógica é
realizada por cada circuito?
Exemplo: Diodos ideais
Assumindo que os diodos são ideais, encontre os valores de I
e V nos circuitos da figura abaixo.
Exemplo: Diodos ideais (2)
Procedimento a ser adotado: (1) assumir um comportamento
plausível; (2) proceder com a análise; (3) checar se a solução
obtida é plausível.
a
1 suposição: D1 e D2 estão conduzindo 
VB = 0 e V = 0
 ID2 = (10 – 0) / 10 k= 1 mA
 Equação do nó:
B: I + 1 mA = (0 – (-10) ) / 5 k
 I = 1 mA
D1 está conduzindo, conforme assumido
originalmente, e o resultado final é:
 I = 1 mA e V = 0V.
Exemplo: Diodos ideais (3)
Vamos adotar o mesmo procedimento.
 1a suposição: D1 e D2 estão conduzindo  VB = 0 e V = 0
ID2 = (10 – 0) / 5 k = 2 mA
 Equação do nó B: I + 2 mA = (0 – (– 10) ) / 10 k
 I = – 1 mA.
Como isto não é possível (por que?), nossa
suposição inicial está incorreta.
Nova suposição: D1 está cortado e D2 está
conduzindo.
ID2 = (10 – (– 10)) / 15 = 1,33 mA
Tensão no nó B: VB = – 10 + 101,33 = +3,3V
 D1 está reversamente polarizado, conforme
assumido, e o resultado final é I = 0A e V = 3,3V.
Exercício 3.4
Determine os valores de I e V nos circuitos a seguir.
Características terminais de diodos
de junção – característica i  v
Características terminais de diodos
de junção – característica i  v (2)
Características terminais de diodos
de junção – característica i  v (3)
3 regiões distintas:
1. A região de polarização direta (v > 0)
2. A região de polarização reversa (v < 0)
3. A região de avalanche (breakdown) (v < - VZK)
1- A região de polarização direta: tensão terminal v é positiva.

Nesta região, a relação
i  v pode ser aproximada por:

i  Is e
v / nVT

1
Região de polarização direta


i  I s ev / nVT  1
IS : corrente de saturação reversa (ou corrente de escala:
corrente diretamente proporcional à seção transversal da
área do diodo).
•
Para diodos de pequenos sinais (aplicações de baixa
potência): IS  10 – 15 A
•
IS : varia fortemente em função da temperatura.
(IS dobra de valor a cada aumento de 5oC na temperatura,
aproximadamente).
kT
VT: tensão térmica (constante): VT 
q
k: constante de Boltzmann = 1,3810-23 J/K
T: temperatura absoluta em Kelvin = 273 + temperatura em oC
q: magnitude da carga do elétron = 1,6010-19 C
Região de polarização direta (2)

i  Is e
v / nVT

1
À temperatura ambiente (20oC), VT = 25,2 mV.
•
Para análises aproximadas rápidas, vamos utilizar VT 
25 mV à temperatura ambiente (em 25oC, VT  25,8 mV)
n (constante): para um diodo, 1  n  2. Em geral, vamos
assumir n = 1 (em CIs; n = 2 em componentes discretos)
i >> IS :
i  Is e
v / nVT
i
 v  nVT ln
Is
Região de polarização direta (3)
i  Is e
v / nVT
i
 v  nVT ln
Is
Considere a relação i  v na equação anterior:
 corrente I1 correspondendo a uma tensão no diodo V1:
I1  I s eV1 / nVT
 corrente I2 correspondendo a uma tensão no diodo V2:
V2 / nVT
I2  Is e
 I2 
I2
(V2 V1 ) / nVT
 e
 V2  V1  nVT ln 
I1
 I1 
Região de polarização direta (4)
 I2 
 I2 
V2  V1  nVT ln   V2  V1  2,3 n VT log 
 I1 
 I1 
 Para uma mudança de uma década (um fator de 10) na
corrente, a queda de tensão no diodo varia de um fator de
2,3nVT
 n = 1   60mV ; n = 2   120mV (curva
característica: gráfico semilog: v (linear)  i (log) 
linha reta com inclinação de 2,3nVT por década de
corrente).
 Sem o conhecimento de n: inclinação de  0,1V/dec
costuma ser utilizada.
Região de polarização direta (5)
 Da curva característica i  v : corrente muito pequena para
tensões menores do que  0,5V  tensão de joelho do diodo
(conseqüência da relação exponencial entre i e v ).
 Diodo diretamente polarizado em “condução total”: queda
de tensão entre 0,6 e 0,8 V, aproximadamente  custumase utilizar 0,7V em modelos de diodos (de silício).
 Diodos com diferentes correntes nominais de operação (ou
seja, com áreas diferentes e, conseqüentemente, IS
diferentes), exibirá esta queda de 0,7V em diferentes
correntes.
 Diodos de pequenos sinais: 0,7V em i = 1mA
 Diodos de alta potência: 0,7V em i = 1A.
Exemplo 3.3
Um diodo de silício de 1mA possui uma queda de tensão
direta de 0,7V na corrente de 1mA. (a) Avalie a constante de
escala de junção IS no caso de se ter n = 1 ou n = 2. (b) A
seguir, determine que constantes de escala seriam aplicáveis
para um diodo de 1A do mesmo fabricante que conduz 1A com
0,7V.
v / nVT
v / nVT
iI e
 I ie
s
s
(a) Para o diodo de 1mA:
• n = 1:
• n = 2:
3
I s  10 i e
700 / 25
 6,9 10
16
A  10
15
A
I s  103 i e700 / 50  6,3 1010 A  109 A
(b) Diodo conduzindo 1A com 0,7V: corresponde a 1000 diodos
de 1mA em paralelo, com uma área de junção 1000 vezes
maior  IS é 1000 vezes maior, 1pA e 1mA para n = 1 e n = 2,
respectivamente.  O valor de n é importante!
A característica i-v e a temperatura
IS e VT são funções da temperatura  a característica i-v
direta varia com a temperatura.
 Para uma corrente constante no diodo  a queda de
tensão em seus terminais decresce de aproximadamente
2mV para cada aumento de 1oC na temperatura.
A região de polarização reversa
Polarização reversa: v < 0

i  Is e
v / nVT

1
 Se v < 0 e maior do que VT  o termo exponencial da
expressão da corrente no diodo torna-se desprezível comparado
à unidade  i  – IS : a corrente de polarização reversa é
constante e igual a IS  corrente de saturação reversa.
 Em diodos reais: a corrente de saturação reversa > IS .
 A corrente de saturação reversa aumenta um pouco com o
aumento da tensão de polarização reversa.
 Corrente de saturação reversa: proporcional à área da junção
(assim como IS ).
 Dependência com a temperatura: a corrente de satuação
reversa dobra para cada aumento de 10oC na temperatura,
aproxim. (IS dobra para cada aumento de 5oC na temperatura).
Exercício 3.9
O diodo no circuito da figura abaixo é um dispositivo grande e
de elevada corrente cuja corrente de polarização reversa é
razoavelmente independente da tensão aplicada. Se V = 1V a
20oC, determine o valor de V a 40oC e a 0oC.
Resposta: 4V; 0,25V.
A região de avalance (breakdown)
O diodo entra nesta região de condução quando a magnitude
da tensão reversa ultrapassa um valor limite específico para o
diodo em particular: tensão de avalanche (tensão de “joelho” na
polarização reversa): VZK
Nesta região, a corrente reversa aumenta rapidamente, sem
que haja um aumento significativo da tensão associada.
A operação nesta região não é necessariamente destrutiva,
contanto que a potência dissipada no diodo seja limitada por um
circuito externo a um nível seguro (especificado no datasheet do
fabricante).
Tensão reversa praticamente constante: EFEITO ZENER
Operação física de diodos
– Semicondutores
http://www.comp.ufla.br/~giacomin/Com145/Diodo_semicond.pdf
As propriedades elétricas dos semicondutores são afetados por variação
de temperatura, exposição a luz e acréscimos de impurezas.
 Silício e germânio: estrutura monocristalina; na indústria eletrônica:
elevado grau de pureza – uma parte para dez bilhões (1:1010).
Semicondutores – Estrutura cristalina
http://www.comp.ufla.br/~giacomin/Com145/Diodo_semicond.pdf
http://ece-www.colorado.edu/~bart/book/book/chapter2/ch2_2.htm
Silício e germânio:
(ligações covalentes)
monocristais
–
estrutura
diamante
Estrutura cristalina do silício
FONTE: http://hyperphysics.phy-astr.gsu.edu/hbase/solids/sili2.html
Posicionamento de átomos de silício em uma célula
unitária – padrão diamante.
Cristal semicondutor com ligações covalentes.
Semicondutores
– Níveis ou bandas de energia
http://hyperphysics.phy-astr.gsu.edu/hbase/solids/sili.html#c3
Silício e germânio: 4 elétrons de valência – modelo atômico
de Bohr:
Semicondutores
– Níveis ou bandas de energia (2)
http://ece-www.colorado.edu/~bart/book/book/chapter2/ch2_3.htm
Bandas de energia da estrutura diamante  constante do
reticulado cristalino:
Bandas de energia do (a) germânio, (b) silício e (c) arseneto de gálio.
Semicondutores
– Diagrama de bandas simplificado
http://ece-www.colorado.edu/~bart/book/book/chapter2/ch2_3.htm
Energia do elétron livre
(fora do cristal)
c: afinidade eletrônica
q: carga do elétron
Energia do “gap”
Energia da banda
de condução (mínima)
Energia da banda
de valência (máxima)
Leituras adicionais
http://www.comp.ufla.br/~giacomin/Com145/Diodo_semicond
.pdf - Introdução ao estudo dos materiais semicondutores.
http://ecewww.colorado.edu/~bart/book/book/chapter2/ch2_1.htm
Chapter 2: Semiconductor fundamentals.
-
http://hyperphysics.phy-astr.gsu.edu/hbase/solids/intrin.html
– Semicondutor intrínseco (siga os demais links a respeito de
semicondutores nesta página)
http://www.playhookey.com/semiconductors/basic_structure.html
semiconductor crystal structure
-
Basic