Parte 2

Circuitos Operadores Matemáticos não lineares
São circuitos que utilizam elementos não lineares para realizar
operações de multiplicação, divisão, logaritmo, exponencial, etc. Esses
circuitos utilizam geralmente um elemento não linear baseado numa junção
semicondutora (diodo ou transistor bipolar).
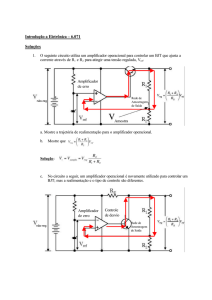
Figura 14: Curva característica de
I D x VD de um diodo de junção semicondutora PN
Modelo matemático de I D = f (VD )
Polarização direta VD ≥ 0
  qVD  
I D = I S  e nkT  −1


kT
VT =
q
Modelo matemático de I S = f (T )
3
 Eg ( qTT ) 
0

 T n 
I S (T ) = I S (T0 )  e  nk (T −T0 ) 
 T0 
Onde:
I S : corrente de saturação reversa (depende de: geometria, temperatura e
semicondutor utilizado);
VD : tensão de polarização direta
q : carga do elétron ( 1,6.10− 19C )
k : constante de Boltzmann ( 1,38.10−23 J K )
T : temperatura absoluta (Kelvin)
Eg : Energia de “bandgap” do semicondutor (1,12 eV para Si)
n : coeficiente de emissão de portadores que dependem do tipo de junção e do
semicondutor. Usualmente encontra-se entre 1 < n < 2.
Obs.: Tipicamente I S dobra para cada 10 graus de aumento da temperatura.
Operador Logaritmo
Realiza a operação de logaritmo neperiano (ln) de uma tensão de
entrada v i .
R1
2
-
Vi
V-
4
D1
Vo
8
+
1
V+
OUT
3
Figura 15: Circuito Amplificador Logaritmo
Id = Ii
V + =V − = 0
Vd
Vd
vi
nVT
nVT
Ii =
Considerando: e
>> 1 ⇒ I d = I S e
R
Vd = −vo
V
I
ln  d
 IS
d

V
I 
nVT
 = ln e
= d ∴Vd = nVT ln  d 
nVT

 IS 
 v 
v o = −nVT ln  i 
 RI S 
Onde: n e R são constantes, porém VT e I S variam com a temperatura
gerando um erro na operação. Para eliminar esse erro é utilizado um circuito de
compensação de temperatura
Ø Compensação de temperatura
Para que o Amplificador Logarítmico funcione em diferentes
temperaturas é necessário um circuito que compense variações de VT e I S .
a) Compensação de I S : usa-se um segundo diodo idêntico polarizado
diretamente com uma corrente constante e conectado à saída do circuito de
modo a subtrair a tensão do diodo D1.
R
2
Vi
-
V-
4
D1
Vo
Vo´
Iref
8
+
V+
OUT
3
D2
1
Figura 16: Circuito de Compensação de temperatura do Amplificador Logaritmo
Consideramos D1 identico a D2 ⇒ I S ´ = I S
 v 
v o = −nVT ln  i 
 RI S 
I d 2 = Iref
 Iref
Vd 2 = nVT LN 
 IS




  Iref
v o´ = Vd 2 + v o = nVT  ln 
  IS
 
 
v o´ = nVT ln 

 
 
Iref
IS
vi
RI S

 v
 − ln  i

 RI

 S






 = nV  ln Iref .I S .R 
T

v i .I S 



Portanto:
 Iref .R 
 vi 
 ou v o´ = − nVT ln 
v o´ = nVT ln 

 vi 
 Iref .R 
b) Compensação de VT : utilisa-se um estágio de amplificação com
ganho variável com a temperatura, através de um resistor (RT) cuja resistência
é função da temperatura.
3
+
D2
Vo´
1
V+
OUT
8
-
3
+
V+
2
OUT
Iref
-
4
8
2
1
V-
R
Vi
V-
4
D1
RF
RT
Figura 17: Circuito de Compensação de
VT do Amplificador Logaritmo
Vo´´
 R 
v o´´ = vo´  1 + F 
RT 

fazendo → R F >> RT
RF
R
 vi 

∴ v o´´ = −nVT F ln 
RT
RT  Iref .R 
R
 vi 
v o´´ = −n.VT . F ln 

RT  Iref .R 
RT deve ser escolhido de modo a possuir uma variação de temperatura que
dRT
dV
compense a variação de VT , ou seja:
= T
RF dT
dT
Pode ser feita uma associação de RT com resistor(es) fixo(s) para abter a
variação adequada.
R
Normalmente faz-se Iref.R=1 e n.VT . F = 1 , de modo a obter-se:
RT
v o´´ = vo´
vo´ = − ln vi
Ø Resposta em freqüência para o amplificador logarítmico
Usando as aproximações:
1 - Diodo ≡ resistor variável
2 - Rd = resistência do diodo variável com a corrente de polarização
Podemos equacionar o circuito do amplificador logarítmico da figura 16 da
seguinte forma:
I 
dV
rd = d
Vd = nVT ln  d 
dI d
 IS 
VT
Id
nV R
∴ rd = T
vi
Para o amplificador inversor temos:
Rv i
v
R
f CS = f T
= fT
∴ f CS = f T i
rd
nVT R
nVT
rd = n
Id =
vi
R
Onde: f CS = freqüência de corte
f T = freqüência de transição do AmpOp
Obs. 1: A freqüência de corte depende da amplitude de entrada v i
Obs. 2: Para tensões de entrada negativas muda-se a polaridade do diodo.
G
a
n
h
o
120
fc
D
i 100
f
e
r
e
n
c
i 80
a
l
(
d
B
)
60
40
20
0
1.0Hz
Vdb(R1:2)+120
10Hz
100Hz
1.0KHz
10KHz
100KHz
1.0MHz
10MHz
Frequency
Figura 18: Resposta em freqüência do circuito amplificador logaritmo ( ganho X freqüência ).
1.3.3 Operador Exponencial
Circuito que realiza a operação de exponencial em uma tensão de
entrada v i .
D
2
Vi
-
V-
4
R
+
Vo
8
3
1
V+
OUT
Figura 19: Circuito amplificador Exponencial
V + =V − = 0
v i = vd
VR
v
R I d = − o ( saída )
R
VR = −v o
entrada :
Id =
Vd
 nV


I d = I S e T − 1




para → Vd >> nVT ⇒ I d = I S e
 vi

 n .VT



Vd
nVT
∴ v 0 = −R.I S .e
Da mesma forma que no amplificador logarítmico, faz-se necessário
compensar as variações de VT e I S com a temperatura através de um circuito
de compensação.
Ø Compensação de temperatura
a) Compensação de I S : usa-se um segundo diodo idêntico polarizado
diretamente com uma corrente constante e conectado à entrada do circuito de
modo a subtrair a tensão do diodo D1.
D2
Vi´´
3
D1
1
2
-
V+
OUT
V-
-
+
OUT
3
+
Vo
8
8
Vi´
1
V+
2
V-
Iref
4
4
R
Figura 20: Circuito amplificador Exponencial com compensação de
IS .
b) Compensação de VT : utilisa-se um divisor de tensão na entrada com
ganho variável com a temperatura, através de um resistor (RT) cuja resistência
é função da temperatura.
D2
Vi´´
3
+
D1
1
2
1
OUT
8
3
+
Vo
Vi´
8
RF
-
V+
OUT
4
-
V-
2
V+
Iref
V-
4
R
Vi
RT
Figura 21: Circuito amplificador Exponencial com compensação de
vi´ = vi
I S e VT .
RT
RF + RT
Para RF >> RT ∴ vi´ = vi
RT
RF
RT deve ser escolhido de modo a possuir uma variação de temperatura que
dRT
dV
compense a variação de VT , ou seja:
= T
RF dT
dT
 v i . RT

 R . n .V
 F
T




Compensação final: vo = − R.Iref .e
R
Normalmente faz-se Iref.R=1 e n.VT . F = 1 , de modo a obter-se: vo´ = −evi
RT
Ø Resposta em Freqüência para amplificador Exponencial
Rd
2
-
V-
4
R
Vi
3
Vo
8
+
1
V+
OUT
Figura 22: Circuito equivalente para determinar a resposta em freqüência.
nVT
Id
r
f
nV
fC = fT d = T ∴ fC = T
R
A
Id R
Temos a resistência dinâmica do diodo D1: rd =
vo = − RI d
vo = RI d
Id =
vo
R
Portanto temos: f C = f T =
G 120
a
n
h
o
nVTT
vo
fc
D
i 100
f
e
r
e
n
c
i 80
a
l
(
d
B
)
60
40
20
0
1.0Hz
Vdb(R1:2)+120
10Hz
100Hz
1.0KHz
10KHz
100KHz
Frequency
Figura 23: Resposta em Freqüência do amplificador exponencial.
1.0MHz
10MHz
Ø Amplificadores log e exp com transistores
Transistores podem ser usados como diodos nos amplificadores log e exp,
possibilitando algumas melhorias:
• Maior faixa dinâmica (amplitude) que os amplificadores a diodo;
• Maior “linearidade” da função.
Para consulta adicional:
www.electronics.dit.ie/staff/ypanarin/Lecture Notes/DT021-4/6AntiAndLogAmplifiers(4p).pdf
Ø Mudança de base em amplificadores log
As junções semicondutoras possuem sempre comportamento
exponencial com base neperiana. Para obter amplificadores log com base
qualquer, utiliza-se um circuito adicional dimensionado a partir das
propriedades de mudança de base de logaritmo.
Temos que:
log A x
log B x =
.
log A B
ln x
Considerando A como sendo a base neperiana: log B x =
ln B
Assim para obter-se log B v i , faz-se:
ln v i
onde ln B é uma constante e pode ser facilmente implementada com
ln B
amplificadores (quando lnB <1) ou divisores de tensão (quando lnB >1).
Exemplo 02): Encontre v o sabendo que v o = log 10 vi e B = 10 .
Solução:
ln Vi
Vo=ln Vi
Vi
R2
Vo=log10 Vi
R1
Figura 24: Figura exemplo 02
v o = vo´
R1
R1 + R2
vo
1
=
vo´ ln 10
R1
= ln 10 = 2,303
R1 + R2
Arbritando R1 e calculando R2 temos: R1 = 1KΩ e R2 = 1,3 KΩ
Exemplo 03) Usando B = 2 determine v o = log 2 vi
Solução:
Vo´
R1
2
Vi
-
V-
ln Vi
4
R2
Vo
8
+
1
V+
OUT
3
Figura 25: Figura exemplo 03
ln 2 = 0,693 < 1
R 
R
−1
R
v o = −vo  2  ⇒ − 2 =
∴ ln 2 = 1
R1 ln 2
R2
 R1 
vo
R
−1
=
⇒ 1 = ln 2 = 0,693
vo´ ln 2
R2
se R1 = 10 KΩ temos R2 = 14,43KΩ
Obs.: Este circuito inversor compensa a polaridade negativa da saída do
amplificador logaritmo.