Capítulo 4 – Séries de Fourier Dizemos que representamos

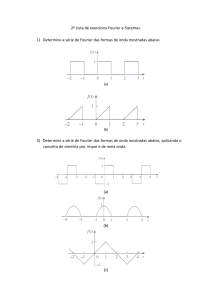
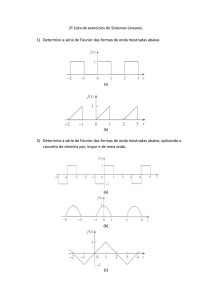
Capítulo 4 – Séries de Fourier
Dizemos que representamos uma função real
ela se expressa na série
em série de Fourier quando
os coeficientes
são chamados de coeficientes de Fourier. Claro, a série
de Fourier só poderá representar rigorosamente
, se esta função for
periódica com período igual a
. Caso contrário, a série de Fourier
representará (bem ou aproximadamente bem se a função tiver
descontinuidade) apenas nesse intervalo.
Como veremos adiante, podemos facilmente mudar o intervalo –
valor arbitrário –
para um
. A série de Fourier é a base ortonormal mais simples
(composta por funções senos e cossenos ortogonais) de representar funções
num espaço vetorial de dimensão infinita (espaço de Hilbert). Funções serão na
verdade, vetores neste espaço que está munido de produto escalar. Logo,
podemos, neste espaço, falar em uma função
ser perpendicular a outra
, no intervalo
, quando
Vejamos
a
ortogonalidade
Multiplicando (1) por
no
espaço
de
Fourier
e integrando no intervalo –
.
, temos
pois as integrais em cosseno e seno se anulam. Logo,
1
Multiplicando (1) por
temos
e integrando no intervalo –
,
Das relações trigonométricas:
i)
seguem
e
ii)
seguem
e
A 1ª. integral do 2º. membro de (3) é nula.
A 2ª. integral do 2º. membro de (3)
A 3ª. integral do 2º. membro de (3)
Logo,
ou seja
2
e integrando no intervalo –
Multiplicando (1) por
temos
,
A 1ª. integral do 2º. membro de (7) é nula.
A 2ª. integral do 2º. membro de (7)
A 3ª. integral do 2º. membro de (7)
Logo,
ou seja
As funções
formam uma base completa ortonormal num espaço
vetorial de dimensão infinita (Hilbert). Os senos (cossenos) com diferentes
argumentos são perpendiculares entre si e perpendiculares a qualquer cosseno
(seno). O produto escalar tem a forma
3
Exemplos:
1)
Logo,
A representação em série de Fourier
–
só coincide com
no intervalo
.
f(x)
2)
f(x) é a função escada
+1
-1
x
(pois f(x) é função ímpar)
Para toda função ímpar
podemos escrever
para a função escada
Logo,
4
Observe que em
,
que é a média aritmética dos limites de
à esquerda e à direita da origem, isto é,
.
Propriedade:
Se
tem uma descontinuidade em
então
Período:
Podemos expandir a série de Fourier num período arbitrário
comprimento arbitrário .
(tempo) ou num
Se em (6) e (8) fizermos a mudança de variável
, logo o período é arbitrário
Se em (6) e (8) fizermos a mudança de variável
, logo o período é arbitrário
5
Fourier Seno e Fourier Cosseno
Se uma função
é par de (12a) e (12b) teremos
As equações (13a) e (13b) são a representação Fourier Cosseno de uma
função
.
Se uma função
é ímpar de (12a) e (12b) teremos
As equações (14a) e (14b) são a representação Fourier Seno de uma função
.
f(x)
1
Exemplo:
1/2
-L
L
x
A série de Fourier será
6
A série de Fourier Seno será
A série de Fourier Cosseno será
Os gráficos de
estão mostrados na figura abaixo
7
Forma Complexa da Série de Fourier
Mas
Substituindo em (15)
Definindo as variáveis complexas
Reescrevemos
Multiplicando (16) por
e integrando os 2 lados em
, temos
Logo,
8
Convergência pela Média
Uma grandeza física quando medida experimentalmente (N vezes) assume
valores
. O desvio quadrático médio é definido por
onde
é o valor médio definido por
O Método dos Mínimos Quadrados minimiza esse desvio. Por exemplo,
suponha que 2 grandezas físicas tenham uma relação funcional qualquer, e.g. ,
a magnetização M e a temperatura T; M = M(T). Para cada medida da
temperatura
obtemos uma correspondente magnetização
. Vamos supor
que a relação funcional seja uma reta teórica (só para facilitar, poderia ser
qualquer outra curva),
. Representaremos as variáveis teóricas
por
(correspondendo a ) e
(correspondendo a
). Elas satisfazem a
equação da reta
variáveis experimentais por
a
Equivalentemente, representaremos as
(correspondendo a ) e (correspondendo
experimental). Elas flutuam em torno da reta, i.e.,
.
O desvio quadrático médio entre os valores teóricos e experimentais vale
Para minimizar
, derivamos parcialmente em relação ao coeficiente angular
da reta , e igualamos a zero. Teremos
ou
9
Derivando parcialmente em relação ao coeficiente da reta
zero. Teremos
, e igualamos a
ou
As equações (20b) e (20d) formam um sistema linear (não homogêneo) para as
incógnitas e . A solução é
Podemos utilizar essas idéias para otimizar uma série de Fourier
truncada que representa uma função dada
O desvio quadrático será
ou seja,
Os mínimos ocorrerão em
10
Portanto, o mínimo ocorre quando os coeficientes são de Fourier, isto é,
Substituindo esses coeficientes em
temos
Logo, temos a Desigualdade de Bessel
Se no limite
,
então obtemos a Equação de Parseval
Para as funções
seccionalmente contínuas vale a equação (25) e dizemos
que a base de Fourier forma uma base completa.
11