Triângulos ― classificação

Triângulos ― classificação
Quanto aos ângulos
Quanto aos lados
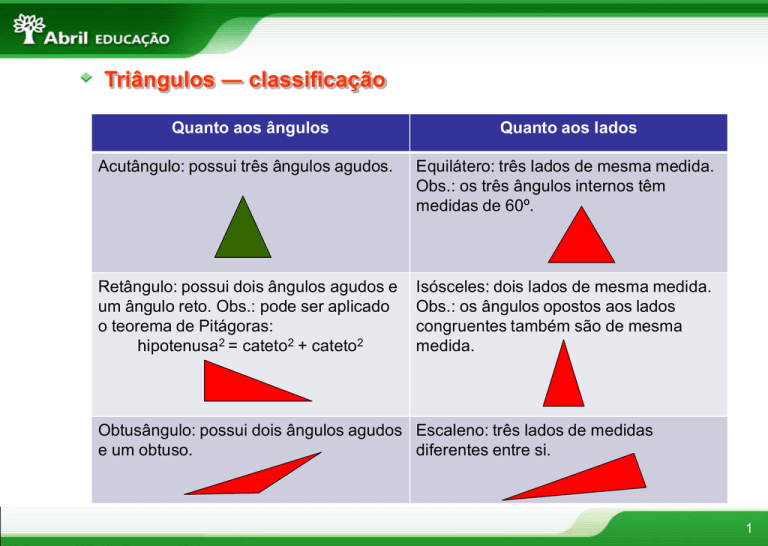
Acutângulo: possui três ângulos agudos.
Equilátero: três lados de mesma medida.
Obs.: os três ângulos internos têm
medidas de 60º.
Retângulo: possui dois ângulos agudos e
um ângulo reto. Obs.: pode ser aplicado
o teorema de Pitágoras:
hipotenusa2 = cateto2 + cateto2
Isósceles: dois lados de mesma medida.
Obs.: os ângulos opostos aos lados
congruentes também são de mesma
medida.
Obtusângulo: possui dois ângulos agudos Escaleno: três lados de medidas
e um obtuso.
diferentes entre si.
1
Triângulos - medidas de seus ângulos
Soma das medidas dos
ângulos internos
a + b + g = 180º
Teorema do ângulo externo
a + x = 180º
b+g=x
Condição de existência de um triângulo
A soma das medidas
dos dois lados menores
tem que ser maior que
a medida do lado maior.
b+c>a
2
Triângulos – cevianas e pontos notáveis
Ceviana
Definição
Mediana
É o segmento que tem como
extremidade um vértice do
triângulo e o ponto médio do lado
oposto a esse vértice.
Baricentro (G): é o ponto de
encontro das medianas do
triângulo; é o centro de
gravidade do triângulo.
É o segmento que tem uma
extremidade em um vértice do
triângulo, divide o ângulo ao meio
e tem a outra extremidade no
lado oposto a esse vértice.
Incentro (I): é o encontro das
bissetrizes internas do
triângulo; é o centro da
circunferência inscrita no
triângulo, pois equidista dos
três lados.
É o segmento com uma
extremidade em um vértice e a
outra extremidade no lado oposto
ou no seu prolongamento,
formando com ele ângulos retos.
Ortocentro (H): é o ponto de
encontro das retas que contêm
as alturas, podendo pertencer
ao exterior do triângulo.
Reta que passa pelo ponto médio
de um lado do triângulo e é
perpendicular a ele.
Circuncentro (C): é o ponto
de encontro das mediatrizes
dos lados do triângulo; é o
centro da circunferência
circunscrita ao triângulo, pois
equidista dos três vértices.
Bissetriz
Altura
Mediatriz
Ponto notável
Figura
3
Congruência de triângulos
Dois triângulos são congruentes se coincidem ao serem
sobrepostos. Isso significa que seus lados, dois a dois, terão a
mesma medida e o mesmo ocorrerá com os seus ângulos.
1o caso: LAL
Dois lados congruentes
e o ângulo formado
por eles congruente
2o caso: LLL
Três lados congruentes
3o caso: ALA
Dois ângulos
congruentes e o lado
compreendido entre
eles congruente
4o caso: LAAo
Um lado congruente,
um ângulo adjacente e
o ângulo oposto a esse
lado congruente
4
Semelhança de triângulos
Dois triângulos são semelhantes se, e somente se, possuem os três ângulos
ordenadamente congruentes e os lados homólogos proporcionais.
Dessa forma, basta verificar alguns elementos para saber se os dois triângulos são
semelhantes.
Assim teremos:
AB BC AC
Casos de semelhança:
=
=
= constante
DE EF DF
1o caso: AA
Se dois ângulos de um
triângulo são
respectivamente
congruentes a dois ângulos
de outro, o terceiro ângulo
também será.
2o caso: LLL
Dois triângulos são
semelhantes se os lados de
um são proporcionais aos
lados do outro.
3o caso: LAL
Dois triângulos são
semelhantes se possuem
um ângulo congruente
compreendido entre lados
proporcionais.
5
Relações métricas no triângulo retângulo
Considere um triângulo ABC, retângulo em A, e o segmento AD
perpendicular ao lado BC , com D em BC .
Definições dos segmentos:
BC = hipotenusa (medida "a")
AB = cateto (medida "c")
AC = cateto (medida "b")
BD = projeção do cateto AB
sobre a hipotenusa (medida "m")
DC = projeção do cateto AC
sobre a hipotenusa (medida "n")
Assim teremos:
a2 = b2 + c 2
a h = b c
b2 = m  a
c2 = n a
h2 = m  n
AD = altura relativa à
hipotenusa (medida "h")
6
Quadriláteros
São polígonos de quatro lados em que a soma das medidas dos ângulos internos é 360º.
Paralelogramo
Retângulo
Losango
Quadrado
Quanto aos
ângulos
Quanto às
diagonais
Quanto aos
lados
Ângulos opostos
congruentes e
ângulos
adjacentes
suplementares.
Encontram-se no
seu ponto médio.
Lados opostos
congruentes.
Quatro ângulos
retos.
São congruentes.
Lados opostos
congruentes.
Ângulos opostos
congruentes e
ângulos
adjacentes
suplementares.
São perpendiculares
entre si e estão
contidas nas
bissetrizes dos
ângulos internos do
losango.
Quatro lados
congruentes.
Quatro ângulos
retos.
Encontram-se no
seu ponto médio e
são congruentes.
Quatro lados
congruentes.
7
Quadriláteros
Os trapézios são quadriláteros que têm apenas um par de
lados paralelos, chamados base maior e base menor.
Trapézio retângulo
É todo trapézio que tem dois
ângulos retos. Nele, um dos
lados que não é base é
perpendicular às duas bases.
Trapézio isósceles
É todo trapézio que tem dois
lados não paralelos
congruentes.
8