Aplicações das funções trigonométricas no estudo de fenômenos

Aplicações das funções trigonométricas no estudo de fenômenos
periódicos
Aparecido Giovani Mariano da Silva, Ermínia de Lourdes Campello Fanti, Flávia Souza Machado da
Silva, Évelin Meneguesso Barbaresco. Campus de São José do Rio Preto, Instituto de Biociências,
Letras e Ciências Exatas - IBILCE, Matemática, [email protected]. Bolsa de Extensão
Universitária – PROEX - Projeto Laboratório de Matemática.
Palavras Chave: Funções trigonométricas, GeoGebra, Fenômenos periódicos.
Introdução
As funções trigonométricas são muito importantes
para o estudo de fenômenos periódicos físicos e
sociais, entre eles temos a claridade exercida pelo
sol em uma cidade ao longo do ano, a variação da
temperatura em uma determinada localidade da
Terra, o fenômeno das marés, a frequência cardíaca
e outros. Uma importante ferramenta para o estudo
da trigonometria e das funções trigonométricas é o
software GeoGebra, que é livre e de fácil manuseio.
Objetivos
O presente trabalho tem como objetivo mostrar como as funções trigonométricas podem auxiliar no
entendimento e resolução de alguns problemas do
cotidiano que envolvem fenômenos periódicos e
analisar os gráficos de tais funções usando o software GeoGebra.
Material e Métodos
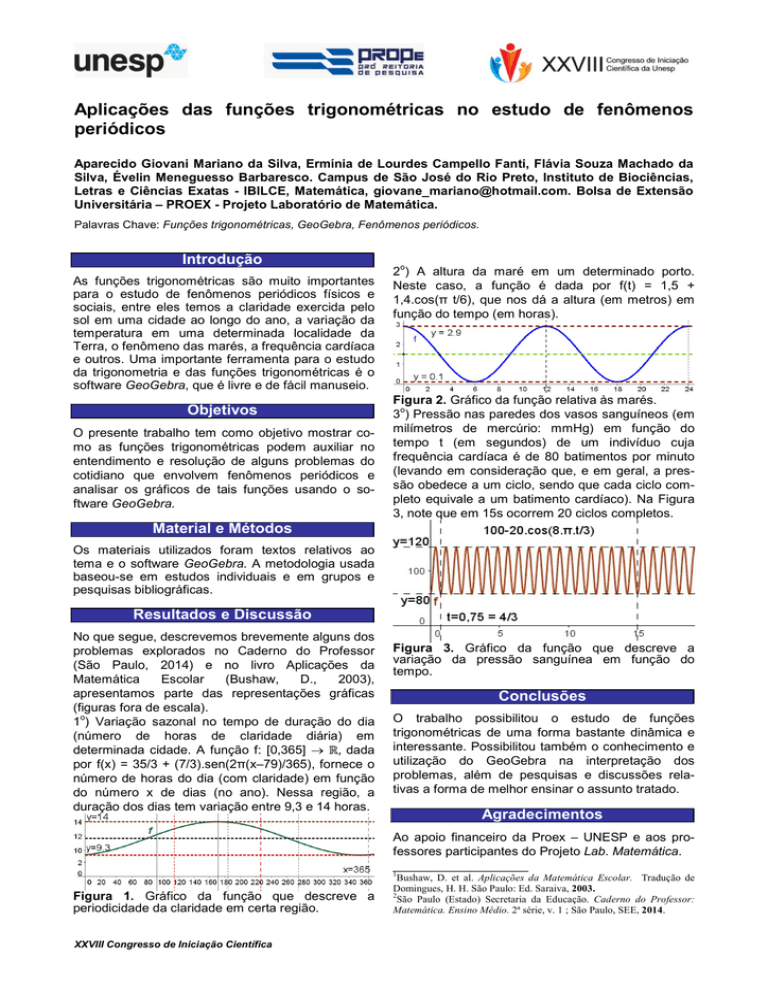
2 ) A altura da maré em um determinado porto.
Neste caso, a função é dada por f(t) = 1,5 +
1,4.cos(π t/6), que nos dá a altura (em metros) em
função do tempo (em horas).
o
Figura 2. Gráfico da função relativa às marés.
o
3 ) Pressão nas paredes dos vasos sanguíneos (em
milímetros de mercúrio: mmHg) em função do
tempo t (em segundos) de um indivíduo cuja
frequência cardíaca é de 80 batimentos por minuto
(levando em consideração que, e em geral, a pressão obedece a um ciclo, sendo que cada ciclo completo equivale a um batimento cardíaco). Na Figura
3, note que em 15s ocorrem 20 ciclos completos.
Os materiais utilizados foram textos relativos ao
tema e o software GeoGebra. A metodologia usada
baseou-se em estudos individuais e em grupos e
pesquisas bibliográficas.
Resultados e Discussão
No que segue, descrevemos brevemente alguns dos
problemas explorados no Caderno do Professor
(São Paulo, 2014) e no livro Aplicações da
Matemática
Escolar
(Bushaw,
D.,
2003),
apresentamos parte das representações gráficas
(figuras fora de escala).
o
1 ) Variação sazonal no tempo de duração do dia
(número de horas de claridade diária) em
determinada cidade. A função f: [0,365]  ℝ, dada
por f(x) = 35/3 + (7/3).sen(2π(x–79)/365), fornece o
número de horas do dia (com claridade) em função
do número x de dias (no ano). Nessa região, a
duração dos dias tem variação entre 9,3 e 14 horas.
Figura 3. Gráfico da função que descreve a
variação da pressão sanguínea em função do
tempo.
Conclusões
O trabalho possibilitou o estudo de funções
trigonométricas de uma forma bastante dinâmica e
interessante. Possibilitou também o conhecimento e
utilização do GeoGebra na interpretação dos
problemas, além de pesquisas e discussões relativas a forma de melhor ensinar o assunto tratado.
Agradecimentos
Ao apoio financeiro da Proex – UNESP e aos professores participantes do Projeto Lab. Matemática.
___________________
Figura 1. Gráfico da função que descreve a
periodicidade da claridade em certa região.
XXVIII Congresso de Iniciação Científica
Bushaw, D. et al. Aplicações da Matemática Escolar. Tradução de
Domingues, H. H. São Paulo: Ed. Saraiva, 2003.
2
São Paulo (Estado) Secretaria da Educação. Caderno do Professor:
Matemática. Ensino Médio. 2ª série, v. 1 ; São Paulo, SEE, 2014.
1