Algumas Aplicações da Geometria/Trigonometria.

Algumas Aplicações da Geometria/Trigonometria.
Bruna Flório, Ermínia de Lourdes Campello Fanti, Augusto Sergio Furquim, Bruna de Paula Sousa,
Aparecida Francisco da Silva. Campus de São José do Rio Preto, Instituto de Biociências, Letras e
Ciências Exatas - IBILCE, Matemática, [email protected]. Bolsa BAAE II – Projeto
Laboratório de Matemática.
Palavras Chave: Trigonometria, GeoGebra, Distâncias Inacessíveis.
Introdução
A trigonometria é uma ferramenta importante na
Matemática e está ligada a problemas práticos,
principalmente aos relacionados a cálculo de
distâncias inacessíveis, como por exemplo, a altura
de uma montanha. As funções trigonométricas são
de grande importância na modelagem de fenômenos periódicos. Dentre os diversos fenômenos
periódicos possíveis de serem modelados (usando
seno e cosseno) podemos citar quatro: cálculo do
período de claridade de uma cidade, a periodicidade
da pressão sanguínea a temperatura de
determinada localidade em certas épocas do ano, e
o fenômeno das marés (São Paulo, 2009). Uma
importante ferramenta para o estudo da
trigonometria, principalmente as funções trigonométricas é o GeoGebra. O GeoGebra é um software
livre, de fácil manuseio e pode ser obtido no site
http://www.geogebra.org/cms/pt_BR.
Objetivos
aproximado do raio da Terra (segundo Eratóstenes),
supondo-se que a Terra seja esférica e, usando
conceitos básicos de geometria do plano, pode-se
obter a partir de certos dados, um modelo teórico
que possibilita o cálculo (Lima et al., 2001 e Ávila,
2004): No dia do solstício de verão (no hemisfério
Norte) Erastóstenes verificou que, ao meio dia, o sol
brilhava diretamente dentro de um poço profundo
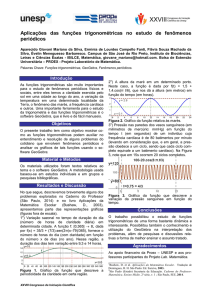
em Siene (hoje Assuã, que indicamos na Figura 1
abaixo por S) e, em Alexandria (A), a 5000 estádios
ao norte de Assuã, alguém mediu o ângulo que os
raios solares faziam com a vertical, encontrando
1/50 do círculo (o que corresponde a 7,2º) Como os
raios solares são praticamente paralelos, isso significa que o ângulo central ACS também mede 7,2°.
O material utilizado foi o software GeoGebra, o
Laboratório Epsylon (Dep. Mat – IBILCE) e softwares para digitação do trabalho. A metodologia usada
baseou-se em estudos individuais e em grupos,
reuniões semanais e pesquisas bibliográficas.
Figura 1: Calculando o raio da Terra
Pela proporcionalidade entre arcos e ângulos, temse 2πR/360 = 5000/7,2, sendo R o raio da Terra.
Considerando que 1 estádio (unidade de medida da
época, referente ao comprimento da pista de corrida
utilizada nos jogos olímpicos da antiguidade) era
equivalente a 1/10 de milha, aproximadamente 160
metros e tomando π ≈3,14, obtém-se R≈ 6.369 km,
e que o comprimento da “circunferência da Terra” é
aproximadamente 40.000 km, que é um resultado
muito bom. Como um exemplo de modelagem de
fenômenos periódicos, tem-se a função f(t) = 1,8+
0,7sen(2πt)/13, com t em dias e y= f(t) em metros,
que pode ser usada para modelar as alturas, em
metros, das marés altas no porto de Recife por
determinado período (a partir de dados observados,
das alturas das marés, durante os meses de
agosto/setembro de 2004) (São Paulo, 2009).
Resultados e Discussão
Conclusões
Foram elaboradas atividades para explorar, com o
uso do GeoGebra, conteúdos como razões
trigonométricas no triângulo retângulo e gráficos de
funções trigonométricas. Tais atividades foram
apresentadas numa Oficina realizada no IBILCE
(Lab. Informática Epsylon), para alunos de 1ª e 2ª
séries de E. Médio da E.E. Monsenhor Gonçalves SJRP. O interesse/participação dos alunos foi muito
bom. Através da dinâmica do software os conceitos
tratados foram melhor entendidos. Para o cálculo
Este trabalho possibilitou o aprendizado de
resultados importantes de trigonometria e geometria.
O presente trabalho teve por objetivo explorar
conceitos trigonométricos sobre dois aspectos: (1º)
utilizando o software GeoGebra no estudo de razões
trigonométricas no triângulo retângulo, e funções
trigonométricas (gráficos); (2º) através de problemas
concretos, dentre eles destacamos o cálculo do raio
da “circunferência” da Terra, segundo pensamentos
e critérios do matemático Eratóstenes de Alexandria
(276 – 196 a.C) e a modelagem de certos fenômenos periódicos.
Material e Métodos
XXV Congresso de Iniciação Científica
Agradecimentos
Ao apoio financeiro da Proex - UNESP- B. BAAE II.
__________________________________________
1
Lima, E.L. et al. Temas e Problemas. SBM, Rio de Janeiro. 2001.
São Paulo (Estado) Secretaria da Educação. Caderno do Professor:
Matemática. Ensino Médio. 2ª série, v. 1 ; São Paulo, SEE, 2009.
3
Ávila, G. Se eu fosse professor de Matemática. RPM n. 54, 2004, 2-9.
2