0.26 Corrente de deslocamento de Maxwell: lei de Amp`ere

0.26. CORRENTE DE DESLOCAMENTO DE MAXWELL: LEI DE AMPÈRE-MAXWELL111
0.26
Corrente de deslocamento de Maxwell: lei de
Ampère-Maxwell
0.26.1
”Estado da arte”
As equações básicas que governam o comportamento das cargas eléctricas, estudadas até
agora, são as seguintes:
A lei de Gauss, que estudámos no âmbito da electrostática, mas que é uma lei geral
também da electrodinâmica:
∇·E=
ρ
0
(334)
A lei de Faraday, que é já uma lei electrodinâmica:
∇×E =−
∂B
∂t
(335)
A inexistência de cargas magnéticas:
∇·B=0
(336)
A lei de Ampère, que estudámos no âmbito da magnetostática e que, conforme veremos,
se aplica exclusivamente neste âmbito:
∇ × B = µ0 J
(337)
A ligação dos campos eléctrico e magnético governados por estas leis ao comportamento das cargas é feita através da expressão que, em rigor, serve de definiç ao dos
campos - a expressão da força de Lorentz:
F = q (E + v × B)
(338)
Finalmente, acresce um outro princı́pio fundamental obsevado na Natureza, que é o
princı́pio da conservação da carga eléctrica, traduzido na equação local:
∇×J=−
∂ρ
∂t
(339)
112
0.26.2
Problemas da lei de Ampère em electrodinâmica
A lei de Ampère da magnetostática claramente enfrenta problemas em situações em que
∂i/∂t = 0. O exemplo clássico é o da carga de um condensador de capacidade C através
de uma resistência R, usando uma fonte de tensão V . Conforme sabemos, o condensador
carrega progressivamente até à carga final Q = CV , sendo a carga nas placas no instante
t descrita pela equação:
sendo a corrente no circuito:
q(t) = CV 1 − e−t/RC
(340)
dq(t)
V
= e−t/RC
dt
R
(341)
i(t) =
Esta corrente tende para zero quando t → ∞, que corresponde à situação estacionária
em que o condensador está completamente carregado, não havendo corrente no circuito.
No entanto, durante o transitório temos corrente no circuito, descrita pela eq. (341).
Conforme sabemos, esta corrente corresponde à transferência de carga entre as placas do
condensador, realizada pela fonte de tensão, não havendo em momento algum corrente a
atravessar o dieléctrico que separa as placas (assumido como um perfeito isolador).
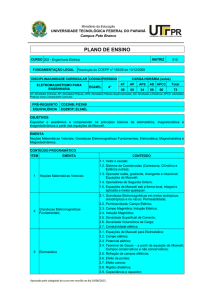
Consideremos agora, tal como exemplifica a figura 23, um circuito de Ampère centrado
num elemento do fio que liga a bateria a uma das placas do condensador. A lei de Ampère,
na sua forma integral, afirma que a circulação do campo magnético no circuito de Ampère
é simplesmente proporcional à corrente que atravessa uma superfı́cie qualquer assente no
circuito de Ampère. É precisamente aqui que reside o problema na aplicação da lei de
Ampère a este problema: é que, enquanto durar a carga do condensador, as superfı́cies
intersectadas pelo fio que liga a bateria ao condensador são atravessadas pela corrente I,
enquanto que as superfı́cies que intersectam o dieléctrico, assentes no mesmo circuito de
Ampère, não são atravessadas por qualquer corrente.
Circuito de
Ampère
Condensador
Bateria
Figure 23: Diagrama ilustrando as dificuldades da lei de Ampère na resolução do processo
de carga de um condensador.
0.26. CORRENTE DE DESLOCAMENTO DE MAXWELL: LEI DE AMPÈRE-MAXWELL113
0.26.3
A lei de conservação da carga e a corrente de deslocamento de Maxwell
Maxwell reconheceu que as dificuldades da lei de Ampère advêm do facto de ser incompatı́vel com a lei de conservação da carga eléctrica, conforme já tivémos ocasião de
sublinhar. De facto, temos:
(342)
∇ · (∇ × B) = µ0 ∇ · j
Atendendo ao resultado geral do c’alculo vectorial ∇ · (∇ × B) = 0, resulta imediatamente a condição caracterı́stica da magnetostática:
∇·j=0
(343)
Maxwell investigou a forma de compatibilizar a lei de Ampère com a lei de conservação
da carga eléctrica. Para isso, considerou a alteração necessária para que a lei de Ampère
contivesse em si a lei de conservação da carga eléctrica (339). Para tal, há necessidade de
acrescentar um termo da forma µ0 ∂ρ/∂t à divergência da lei de Ampère:
∇ · (∇ × B) = µ0
∂ρ
∇·j+
∂t
=0
(344)
Este novo termo pode ser entendido tem as dimensões de uma divergência de uma densidade de corrente, e corresponde a acrescentar um termo com as dimensões de densidade
de corrente à lei de Ampére, isto é:
∇ × B = µ0 J + µ0 JMax
(345)
em que
∇ · JMax =
∂ρ
∂t
(346)
Atendendo à lei de Gauss, podemos reescrever:
∇ · JMax
∂ (0 ∇ · E)
∂E
∂E
=
= ∇ · 0
⇒ JMax = 0
∂t
∂t
∂t
(347)
114
A lei de Ampère modificada, designada também lei de Ampère-Maxwell, resulta assim:
∂E
∂t
ou, na forma integral (por aplicação do teorema de Stokes):
∇ × B = µ0 J + µ0 0
B · dl = µ0
(J + JMax ) · dS = µ0 Iint + µ0 0
(348)
∂E
· dS
∂t
(349)
O termo acrescentado por Maxwell, proporcional a ∂E/∂t, designa-se tradicionalmente
por corrente de deslocamento (de Maxwell). Trata-se mais uma vez de uma designação
historicamente consagrada, mas fonte de possı́veis equı́vocos, pois não corresponde a uma
corrente, isto é, a um trânsito de cargas.
Note-se que o argumento avançado por Maxwell para corrigir a lei de Ampère é um
argumento de natureza puramente teórica, tratando-se de um dos mais notáveis exemplos
de um argumento teórico que abre, conforme veremos, todo um novo horizonte a uma área
de investigação, e que através dos subsequentes testes experimentais, abre possibilidades
até então insuspeitas ao conhecimento e à tecnologia. A própria existência de um ramo de
engenharia conhecido por engenharia electrotécnica é disso o mais eloquente testemunho..
O condensador revisitado
Podemos agora ver como a lei de Ampère-Maxwell descreve o processo de carga de um
condensador. Consideremos novamente a figura 23, em que o condensador está a ser
progressivamente carregado, acumulando uma densidade de carga σ(t) = q(t)/A, onde A
é a área das placas. O campo eléctrico entre as placas, conforme sabemos, é simplesmente
E(t) = σ(t)/0 eˆz , sendo nulo no exterior. Procedamos então ao cálculo da circulação
do campo magnético através do circuito de Ampère apresentado na figura, através do
cálculo do fluxo da densidade de corrente generalizada para uma superfı́cie que atravesse
o dieléctrico. Para simplificar, mas sem perda de generalidade, podemos assumir que esta
superfı́cie é cilı́ndrica, de topos de área A igual à área das placas. O fluxo da densidade
de corrente de Maxwell, 0 ∂E/∂t através desta superfı́cie é simplesmente:
∂E
dσ(t)
dq(t) dS
0
· dS =
eˆz · dS eˆz =
= i(t)
(350)
∂t
dt
dt A
A circulação do campo magnético resulta assim, tal como para o caso em que a superfı́cie intersecta o fio que liga a bateria às placas:
B · dl = µ0 i(t)
(351)
115
0.27. AS EQUAÇÕES DE MAXWELL
0.27
As equações de Maxwell
Com a lei de Ampère-Maxwell, fica concluı́do o edifı́cio do electromagnetismo clássico.
Tratando-se de uma das maiores proezas até agora realizadas pelo homem, vale a pena
apresentá-las de forma unificada:
A lei de Gauss:
∇·E=
ρ
0
(352)
A lei de Faraday:
∇×E =−
∂B
∂t
(353)
A inexistência de cargas magnéticas:
∇·B=0
(354)
A lei de Ampère-Maxwell (que inclui já o princı́pio de conservação da carga eléctrica):
∇ × B = µ0 J + µ0 0
∂E
∂t
(355)
Recorda-se novamente a definição dos campos efectuada pela expressão da força de
Lorentz:
F = q (E + v × B)
(356)
116
0.27.1
Equações de Maxwell em meios materiais
Polarização e magnetização dependentes do tempo
Podemos reescrever as equações de Maxwell na presença de meios materiais com propriedades eléctricas e/ou magnéticas. Conforme vimos anteriormente, no caso de materiais polarizáveis electricamente, a polarização (densidade de momento dipolar eléctrico)
dá-nos a medida da densidade de cargas de polarização:
∇ · P = −ρp
(357)
P · n̂ = σp
(358)
E, no caso de materiais magnéticos, a magnetização (densidade de momento dipolar
magnético) dá-nos a medida da densidade de cargas de magnetização:
∇ × M = Jmag
(359)
No caso da cargas de polarização, quando analisámos o assunto na electrostático pressupusémos sempre que o campo eléctrico permanecia constante no tempo, originando uma
polarização também ela constante. No entanto, em situações electrodinâmicas, o campo
eléctrico pode variar no tempo, gerando uma polarização variável no tempo e, logo, uma
variação temporal da densidade de cargas de polarização, a que está necessariamente associada uma corrente de cargas de polarizaç ao. Podemos calcular facilmente essa corrente.
Consideremos um dado ponto do material, onde a polarização é P. Construamos um pequeno cilindro paralelo à polarização, definindo um volume suficientemente pequeno em
torno do ponto para que possamos considerar desprezáveis as variações de polarização no
volume, isto é, para que possamos considerar a polarização constante no volume. Atendendo à forma como construı́mos este cilindro, a polarização será perpendicular aos topos
e paralela à superfiı́cie lateral do cilindro. Então, a densidade superficial de cargas de
polarização será:
σp = 0, na superfiı́cie lateral do cilindro
σp = +P, no topo superior do cilindro
σp = −P, no topo inferior do cilindro
(360)
(361)
(362)
Se houver uma variação temporal da polarização, tal corresponderá a uma variação da
densidade de carga no topo superior, compensada por uma variação simétrica da densidade
117
0.27. AS EQUAÇÕES DE MAXWELL
de carga no topo inferior, através do estabelecimento de uma densidade de corrente entre
os topos. Esta densidade de corrente é assim, simplesmente:
Jp =
∂P
∂σ
∂P
=
⇒ Jp =
∂t
∂t
∂t
(363)
Note-se que esta densidade de corrente de polarização obedece independentemente à
lei de conservação da carga eléctrica, através da correspondente equação de continuidade:
∇ · Jp =
∂ρp
∂∇ · P
=−
∂t
∂t
(364)
Refira-se que, no caso dos materias magnéticos, não havendo cargas magnéticas, os
efeitos na magnetização da variação temporal do campo magnético estão automaticamente
incluı́dos na equação ∇ × M = Jmag .
Equações de Maxwell em função dos campos auxiliares D e H
As equações de Maxwell podem ser reescritas em função dos campos auxiliares D e H,
separando as densidades de carga e de corrente nas suas partes ”livres” e nas partes
devidas à polarização e à magnetização:
ρ = ρl + ρp = ρl − ∇ · P
J = Jl + Jp + Jm = Jl +
(365)
∂P
+∇×M
∂t
(366)
A lei de Gauss reescreve-se então, como anteriormente:
∇·E=
ρ
⇔ ∇ · (0 E + P) = ρl
0
(367)
e a lei de Ampère-Maxwell fica:
∂E
∂∇ · P
∂E
∇ × B = µ0 (Jl + Jp + Jm ) + µ0 0
= µ 0 Jl +
+ ∇ × M + µ0 0
(368)
∂t
∂t
∂t
Obtemos assim o conjunto de equações de Maxwell reescritas para meios materiais:
∇ · D = ρl
(369)
118
∇×E=−
∂B
∂t
(370)
∇·B=0
(371)
∂D
∂t
onde os campos auxiliares D e H são definidos, como anteriormente, por:
∇ × H = Jl +
D = 0 E + P
(372)
(373)
B
−M
(374)
µ0
A resolução deste conjunto de equações requer ainda algum conhecimento sobre o
comportamento da polarização e da magnetização em função dos campos, sendo particularmente úteis as aproximações para materiais lineares, isotrópicos e homogéneos:
H=
P = 0 χe E
(375)
M = χm H
(376)
Forma integral das equações
Recorrendo como e hábito aos teoremas de Gauss e de Stokes, podemos obter facilmente
a forma integral das equações:
D · dS = Ql
(377)
S
d
E · dl = −
B · dS
dt S
λ
B · dS = 0
(378)
(379)
S
d
H · dl = Il +
dt
λ
S
D · dS
(380)
0.27. AS EQUAÇÕES DE MAXWELL
119
Condições de fronteira
A partir das equações escritas na forma integral, também nos é possı́vel obter facilmente
as condiçoes de fronteira na presença de densidade superficiais de carga ou de corrente,
recorrendo à mesma abordagem utilizada anteriormente:
0.27.2
n̂ · (D2 − D1 ) = σl ⇔ D2⊥ − D1⊥ = σl ⇔ divS D = σl
(381)
n̂ × (E2 − E1 ) = 0 ⇔ E2 − E1 = 0 ⇔ rotS E = 0
(382)
n̂ · (B2 − B1 ) = 0 ⇔ B2⊥ − B1⊥ = 0 ⇔ divS B = 0
(383)
n̂ × (H2 − H1 ) = Kl ⇔ H2 − H1 = Kl ⇔ rotS H = Kl
(384)
Formulação das equações de Maxwell em termos do potencial
É possı́vel obter ainda uma outra forma de escrever as equações de Maxwell, em função
do potencial vector A e do potencial escalar V . Esta formulação potencial das leis da
electrodinâmica é particularmente sistética e poderosa e encontra um âmbito de aplicação
particularmente útil na teoria da radiação electromagnética, essencial para domı́nios como
as antenas e as telecomunicações.
A formulação potencial da electrodinâmica começa pela observação que o campo
magnético é um campo solenoidal, de divergência nula, o que permite escrevê-lo como
o rotacional de um potencial vector A:
∇·B =0 ⇐B= ∇×A
(385)
Por outro lado, o campo eléctrico não é agora conservativo (o seu rotacional não é
nulo), o que inviabiliza a relação E = −∇V que encontrámos na electrostática. Contudo,
a partir da lei de Faraday é possı́vel construir um campo conservativo:
∂B
∂∇ × A
∂A
⇔∇×E=−
⇔∇× E+
=0
∇×E =−
∂t
∂t
∂t
(386)
120
O campo E + ∂A/∂t é pois conservativo e pode ser escrito como o gradiente de
uma função potencial escalar (ou como o simétrico do gradiente, atendendo à reverenda
tradição histórica que encontrámos já na electrostática):
E+
∂A
∂A
= −∇V ⇔ E = −∇V −
∂t
∂t
(387)
Esta definição dos petenciais permite-nos reescrever a lei de Gauss e a lei de AmpèreMaxwell:
∇·E=
ρ
∂
ρ
∂
ρ
⇔ −∇2 V −
⇔ ∇2 V +
(∇ · A) =
(∇ · A) = −
0
∂t
0
∂t
0
∂E
∂
∂A
∇ × B = µ0 J + µ0 0
⇔ ∇ × (∇ × A) = µ0 J + µ0 0
−∇V −
∂t
∂t
∂t
(388)
(389)
Atendendo a que ∇ × (∇ × A) = ∇ (∇ · A) − ∇2 A, a lei de Ampère-Maxwell fica:
∂2A
∇ A − µ0 0 2
∂t
2
∂ 2V
− ∇ ∇ · A − µ0 0 2
∂t
= −µ0 J
(390)
O par de equações (388) e (390), juntamente com a definição dos potenciais V e A
(eqs. 385 e 387), contém em si toda a electrodinâmica das equações de Maxwell. Estas
equações podem ser simplificadas atendendo à liberdade de escolha da divergência de A,
que já discutimos anteriormente. Entre as duas escolhas mais populares para a divergência
de A conta-se não só o já nosso conhecido padrão de Coulomb (∇ · A = 0), mas também
o padrão de Lorentz (∇ · A = µ0 0 ∂ 2 V /∂t2 )