apresentação teórica

Unidade Curricular:
Matemática - EIG0003
MIEIG 2013/2014
1ª aula
Prof. Catarina Castro
Gabinete: M304
1
OBJETIVOS ESPECÍFICOS:
Adquirir conhecimentos teóricos e práticos, essenciais, sobre o
cálculo diferencial de funções reais de variável real e algumas das
suas aplicações.
RESULTADOS ESPERADOS:
1 – Saber aplicar as regras da derivação a funções polinomiais,
exponenciais, logarítmicas e trigonométricas. Derivação de
funções racionais.
2 – Calcular a derivada da função composta e aplicá-la a
problemas práticos.
3 – Obter a derivada da inversa de uma função.
2
Programa
Iniciação ao Cálculo.
Derivação:
Regras da derivação: soma, diferença, produto, quociente, etc.
Derivadas de funções polinomiais
Derivadas de funções exponenciais
Derivadas de funções logarítmicas
Derivadas de funções trigonométricas
Derivada da função composta
Derivada da função inversa
3
Bibliografia Principal
Análise Matemática I,
Texto de apoio (Capítulo 1)
Carlos A. Conceição António
Exercícios de revisão de derivadas
Carlos C. António, Catarina F. Castro
Cálculo Volume I e II
Larson, Hostetler & Edwards,
McGraw-Hill Interamericana, 2006. ISBN: 85-86804-56-8 (vol. 1, oitava edição)
4
REGRAS DE AVALIAÇÃO
Obtenção de Frequência
Não exceder o limite de faltas de acordo com as Normas Gerais de
Avaliação em vigor na Faculdade de Engenharia da Universidade do
Porto.
Cálculo da Classificação Final
Classificação obtida no Exame Final da disciplina com a duração de
60 minutos.
Haverá uma prova de substituição através da qual os alunos poderão
melhorar a avaliação.
Data provisória do 1º Exame (sem consulta)
2ª feira, 11 de Novembro de 2013
Data provisória do Exame de Recurso (sem consulta)
2ª feira, 9 de Dezembro de 2013
5
https://sigarra.up.pt/feup/pt/ucurr_geral.ficha_uc_view?pv_ocorrencia_id=332751
6
7
DIFERENCIAÇÃO EM R
1. Revisão de alguns conceitos e resultados
1.1 Conceito de derivada
1.2 Interpretação física do conceito de derivada
1.3 Derivação de funções compostas (regra da cadeia)
1.4 Derivação da função inversa
1.5 Teorema dos acréscimos finitos (ou de Lagrange)
AMI
1.6 Aplicações
8
CONCEITO DE DERIVADA
Considere-se a reta que passa pelos pontos P e Q na Figura.
Esta reta é designada como reta secante do gráfico da função y=f(x) .
Com base na Figura e considerando as coordenadas
P(a, f(a)) e Q(a+h, f(a+h)) pode-se estabelecer a razão incremental:
9
O ponto Q pode situar-se à esquerda ou à direita do ponto P. Considere-se
um ponto genérico Q(x, f(x)) no gráfico da função representada na figura.
Se f(x) é contínua em a, pode-se fazer Q(x, f(x)) tender para P(a, f(a))
fazendo x tender para a, o que por outras palavras equivale a dizer que
a reta secante torna-se tangente ao gráfico da função no ponto P.
10
DEFINIÇÕES
O declive ou coeficiente angular da reta secante também designado como
taxa de variação média
mPQ
f (a + h ) − f (a )
=
h
O declive ou coeficiente angular da reta tangente ao gráfico de uma função f
em P(a, f(a)) é
desde que o limite exista
11
12
13
14
15
Regras da derivação:
soma, diferença, produto e quociente
F(x)=g(x)+h(x)
F’(x)=g’(x)+h’(x)
F(x)=g(x)-h(x)
F’(x)=g’(x)-h’(x)
F(x)=g(x). h(x)
F’(x)=g’(x).h(x)+ g(x).h’(x)
F(x)=g(x)/h(x)
F’(x)=[g’(x).h(x)- g(x).h’(x)] / [h(x)]2
16
Regras de derivação das funções:
potência, logaritmo e exponencial
F(x)=xk
F’(x)=k. xk-1
F(x)=ln(x) , x>0
F’(x)=1/x
F(x)=ex
F’(x)=ex
17
18
Regra de derivação da função composta ou regra da cadeia
F(x)= g(h(x))
F’(x)=g’(h(x)) . h’(x)
z(x)=z(y(x))
Regra de derivação da função inversa
g(h(x))=x
19
Regra de derivação da função composta ou regra da cadeia
F(x)= g(h(x))
F’(x)=g’(h(x)) . h’(x)
z(x)=z(y(x))
Regra de derivação da função inversa
g(h(x))=x
20
Principais FUNÇÕES TRIGONOMÉTRICAS e
suas derivadas:
f(x)
f’(x)
Sen(x)
Cos(x)
Cos(x)
-Sen(x)
Tang(x)
Sec2(x)
Cotang(x)
-Cossec2(x)
Sec(x)
Sec(x) . Tang(x)
Cossec(x)
-Cossec(x) . Cotang(x)
21
O seno é uma função trigonométrica.
Dado um triângulo retângulo com um de seus ângulos internos igual a θ,
define-se
como sendo a razão entre o cateto oposto a θ e a hipotenusa
deste triângulo. Ou seja:
Exemplo: Um triângulo retângulo cuja hipotenusa é de valor 10 e seus catetos
são de valores 6 e 8. O seno do ângulo oposto ao lado de valor 6 é 6/10 , ou
seja, 0.6.
Num círculo trigonométrico unitário, o seno do ângulo
α é a medida do segmento de reta a vermelho.
http://pt.wikipedia.org/
22
O cosseno (usam-se ainda as formas coseno e co-seno) é uma função
trigonométrica.
Dado um triângulo retângulo com um de seus ângulos internos igual a θ,
define-se cos(θ) como sendo a proporção entre o cateto adjacente a θ e
a hipotenusa deste triângulo. Ou seja:
θ
23
Outra função função trigonométrica:
Num triângulo retângulo, define-se tan(θ) ou tg(θ), como sendo a proporção
entre o cateto oposto a θ e o cateto adjacente a θ:
θ
Consequentemente também é dado
pela razão entre o seno e o co-seno:
24
Definição de cotangente de um ângulo:
Num triângulo retângulo, define-se cotan(θ) ou cotg(θ), como sendo a
proporção entre o cateto adjacente a θ e o cateto oposto a θ:
θ
Consequentemente também é dado
pela razão entre o seno e o co-seno:
25
Num círculo trigonométrico unitário:
Seja x um ângulo agudo, a fórmula fundamental da trigonometria
apresenta-se desta forma:
sin2(x) + cos2(x) = 1
26
A secante é uma função trigonométrica definida como
Num triângulo retângulo, a secante de um ângulo agudo corresponde
à razão da hipotenusa pelo cateto adjacente.
27
A co-secante é uma função trigonométrica definida como
Num triângulo retângulo, a co-secante de um ângulo agudo corresponde
à razão da hipotenusa pelo cateto oposto.
28
Num círculo trigonométrico unitário:
Principais corolários da fórmula fundamental da trigonometria:
29
Principais FUNÇÕES TRIGONOMÉTRICAS e
suas derivadas:
f(x)
f’(x)
Sen(x)
Cos(x)
Cos(x)
-Sen(x)
Tan (x)
Sec2(x)
Cotang(x)
-Cossec2(x)
Sec(x)
Sec(x) . Tan(x)
Cossec(x)
-Cossec(x) . Cotan(x)
30
Unidade Curricular:
Matemática - EIG0003
MIEIG 2013/2014
2ª aula
Prof. Catarina Castro
Gabinete: M304
31
Regras de derivação:
1) Regra do Produto:
2) Regra da Potência:
32
Regras de derivação
• 1)
Derivação da potência em que o expoente é uma constante:
( ) = ( )
em que k é uma constante, então a derivada será
=
• 2)
= ( )
′( )
Derivação da exponencial:
( ) = ( ) em que a base é a constante de Néper, a derivada da função
=
= ( )
′( )
• 3) Derivação da potência sendo a base uma constante e o expoente uma função de x:
=
podemos reescrever introduzindo a função exponencial e a sua inversa que é a função
logarítmo:
=
=
=
( )
em que usamos as propriedades dos logarítmos
33
=
• 3) Derivação de
=
=
=
=
=
( )
× ′
( )
e agora já sabemos derivar:
( ) = ( ) ′( ) ln(k)
4) Derivação da potência sendo:
•
a base uma função u(x) e o expoente outra função de v(x):
= ( )
= ( )
(vamos usar o mesmo processo)
=
( )
=
[
]
34
4) Derivação da potência sendo:
• a base uma função u(x) e o expoente outra função de v(x):
= ( )
(vamos usar o mesmo processo)
= ( )
=
=
= ( )
( )
=
[
]
+
= ( )
+
[
[
]
=
′( )
=
( )
+
= ( )
=
=
′( )
É a soma das 2 regras: Regra da exponencial + Regra da potência
35
Exercício de aplicação :
36
37
Exercício de aplicação da Regra de derivação em cadeia:
Enche-se de água à razão de 1 metro cúbico por hora
um depósito em forma de tronco de cone de secção
circular. Tal como está indicado na figura, a altura do
depósito é de 20 metros, o diâmetro da base é de 4
metros e o diâmetro da boca é de 12 metros.
Usando a regra de derivação em cadeia, calcule a razão
de variação do nível de água h quando esta atinge
metade da altura total do depósito?
Resolução:
As variáveis associadas a este problema são:
•
•
•
•
t o tempo,
V o volume de água dentro do depósito,
h o nível de água e
r o raio da superfície de água.
O enunciado dá
/
e pede um
ℎ/ .
38
Exercício de aplicação da Regra de derivação em cadeia:
Resolução:
As variáveis associadas a este problema são: t o tempo, V o volume de água
dentro do depósito, h o nível de água e r o raio da superfície de água.
O enunciado dá-nos
!
= 1#$ /ℎ e queremos calcular
&
.
!
Pela regra de derivação em cadeia temos,
=
Precisamos calcular
&
∙
ℎ
ℎ
, temos que escrever V função de h.
O volume de um cone é 1/3 do volume de um cilindro. O volume de água será
1
1
= π+ , ℎ + 10 . π2, × 10
3
3
39
Pela regra de derivação em cadeia temos,
=
∙
ℎ
ℎ
Precisamos calcular
, temos que escrever V função de h.
&
O volume de um cone é 1/3 do volume de um cilindro. O volume de água será
1
1
= π+ , ℎ + 10 . π2, × 10
3
3
r
O volume V vem função de 2 variáveis r e h. Como queremos derivar V em ordem a
h temos que eliminar a variável r.
Vamos usar a semelhança de triângulos (ou teorema de Thales) para escrever r função de h:
10 10 + ℎ
2 × 10 + ℎ
10 + ℎ
=
⟺+=
=
2
+
10
5
Substituindo
,
10 + ℎ
ℎ + 10
1
1
1
= π
ℎ + 10 . π2, × 10 = π
5
25
3
3
3
Derivando em ordem a h, temos
ℎ + 10 ,
= π
ℎ
25
$
4
. π × 10
3
40
Substituindo para o caso geral, em qualquer instante,
=
ℎ
ℎ
Para o caso particular em que
do depósito, h=10m, tem-se
!
∙
=
ℎ
ℎ + 10
= π
25
25
π ℎ + 10
∙
ℎ
r
∙
= 1#$ /ℎ e ainda h atinge metade da altura total
10 + 10
1 = π
25
ℎ
,
,
,
∙
ℎ = 10m =
ℎ
(ℎ = 10m)
25
m/h
4004
A razão de variação do nível de água h quando esta atinge metade da altura total do
depósito é de aproximadamente 0.020 metros por hora.
41
Exercício de aplicação da Regra de derivação em cadeia:
42
43
44
45
Principais FUNÇÕES TRIGONOMÉTRICAS e suas INVERSAS:
f(x)
f -1(x)
Sen(x)
arcsen(x)
Cos(x)
arccos(x)
Tang(x)
arctg(x)
Cotang(x)
arccotg (x)
Sec(x)
arcsec(x)
Cossec(x)
arccossec(x)
46
FUNÇÕES TRIGONOMÉTRICAS
Num círculo trigonométrico unitário:
Principais corolários da fórmula fundamental da trigonometria:
47
A INVERSA DA FUNÇÃO TRIGONOMÉTRICA SENO É A FUNÇÃO ARCO-SENO:
Considere-se a função f(x)=sen(x), com domínio [-π/2,π/2] e imagem no intervalo [-1,1].
A função inversa de f, diz-se arco cujo seno,
f-1(x) = arcsen(x) ,
domínio [-1,1] e imagem no intervalo [-π/2,π/2]
48
49
50
Demonstração:
51
52
Derivação da função y=arcsen(x)
Considere-se a função f(x)=sen(x),
com domínio [-π/2,π/2]
e imagem no intervalo [-1,1].
A função inversa de f, diz-se arco cujo seno,
f-1(x) = arcsen(x) ,
domínio [-1,1] e imagem no intervalo [-π/2,π/2]
53
Derivação da função y=arcsen(x)
54
A INVERSA DA FUNÇÃO TRIGONOMÉTRICA COSSENO É A FUNÇÃO ARCO-COSSENO:
Considere-se a função f(x)=cos(x), com domínio [0, π] e imagem no intervalo [-1,1].
A função inversa de f, diz-se arco cujo cosseno,
f-1(x) = arcos(x)
domínio [-1,1] e imagem no intervalo [0, π]
55
Derivação da função y=arcos(x)
56
A INVERSA DA FUNÇÃO TRIGONOMÉTRICA TANGENTE É A FUNÇÃO ARCO-TANGENTE:
Considere-se a função f(x)=tg(x), com domínio ]-π/2,π/2[ e imagem no intervalo ]-∞, +∞[
A função inversa de f, diz-se arco cuja tangente,
f-1(x) = arctg(x) ,
Domínio ]-∞, +∞[ e imagem no intervalo ]-π/2,π/2[
57
Derivação da função y=arctg(x)
58
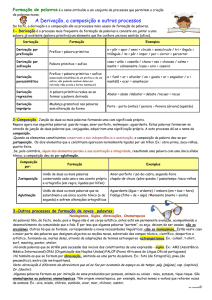
Aprender a demonstrar as seguintes regras de derivação:
59
Unidade Curricular:
Matemática - EIG0003
MIEIG 2013/2014
3ª aula
Prof. Catarina Castro
Gabinete: M304
60
61
Para calcular a derivada da função composta f(x)=u[v(x)]
precisamos considerar a razão incremental
62
63
64
65
66
67
68
69
Exercício de Aplicação da Regra da Cadeia
70
71
DIFERENCIAÇÃO EM R
1. Revisão de alguns conceitos e resultados
1.1 Conceito de derivada
1.2 Interpretação física do conceito de derivada
1.3 Derivação de funções compostas (regra da cadeia)
1.4 Derivação da função inversa
1.5 Teorema dos acréscimos finitos (ou de Lagrange)
AMI
1.6 Aplicações
72
Unidade Curricular:
Matemática - EIG0003
MIEIG 2013/2014
4ª aula
Dúvidas, exercícios e revisões
Prof. Catarina Castro
Gabinete: M304
73