Refração da Luz – Lei de Snell

Refração da Luz – Lei de Snell
1. (Fuvest 2016) Uma moeda está no centro do fundo de uma caixa d’água cilíndrica de
m de altura e base circular com 1,0 m de diâmetro, totalmente preenchida com
0,87 m =
água, como esquematizado na figura.
n1 sen(θ1)  n2 sen(θ2 )
sen(20)  cos(70)  0,35
sen(30)  cos(60)  0,50
sen(45)  cos(45)  0,70
sen(60)  cos(30)  0,87
sen(70)  cos(20)  0,94
Se um feixe de luz laser incidir em uma
direção que passa pela borda da caixa,
fazendo um ângulo θ com a vertical, ele só
poderá iluminar a moeda se
Note e adote:
Índice de refração da água: 1,4 =
a)
b)
c)
d)
e)
θ  20
θ  30
θ  45
θ  60
θ  70
2. (Unesp 2015) A figura representa ondas chegando a uma praia. Observa-se que, à medida
que se aproximam da areia, as cristas vão mudando de direção, tendendo a ficar paralelas à
orla. Isso ocorre devido ao fato de que a parte da onda que atinge a região mais rasa do mar
tem sua velocidade de propagação diminuída, enquanto a parte que se propaga na região mais
profunda permanece com a mesma velocidade até alcançar a região mais rasa, alinhando-se
com a primeira parte.
O que foi descrito no texto e na figura
caracteriza um fenômeno ondulatório
chamado
a) reflexão.
b) difração.
c) refração.
d) interferência.
e) polarização.
www.nsaulasparticulares.com.br
Página 1 de 10
3. (Ufrgs 2015) Na figura abaixo, um raio luminoso i, propagando-se no ar, incide radialmente
sobe placa semicircular de vidro.
Assinale a alternativa que melhor representa a trajetória dos raios r1 e r2 refratados,
respectivamente, no vidro e no ar.
a)
b)
d)
e)
c)
4. (Ufpr 2015) Dependendo das condições do ambiente onde os espelhos devem ser
utilizados, eles são fabricados com um material transparente recobrindo a superfície
espelhada, com o objetivo de protegê-la. Isto aumenta a vida útil do espelho, mas introduz um
deslocamento no ponto onde a luz refletida emerge, se comparado a um espelho não
recoberto. A figura abaixo representa o caminho percorrido por um raio luminoso
monocromático ao incidir sobre um espelho recoberto superficialmente por um material
transparente com espessura T  2mm e índice de refração n2 . O meio 1 é o ar, com índice de
refração n1  1 e o meio 2 possui índice de refração n2  2. Na situação mostrada na figura,
θ1  45.
Considere sen45  cos45  2 2, sen30  1 2 e cos30  3 2.
Utilizando estes dados, calcule a distância D entre a entrada do raio luminoso no meio 2 e sua
saída, assim como está indicada na figura.
www.nsaulasparticulares.com.br
Página 2 de 10
5. (Fgv 2015) Em um laboratório de ótica, é realizada uma experiência de determinação dos
índices de refração absolutos de diversos materiais. Dois blocos de mesmas dimensões e em
forma de finos paralelepípedos são feitos de cristal e de certo polímero, ambos transparentes.
Suas faces de maior área são, então, sobrepostas e um estreito feixe de luz monocromática
incide vindo do ar e no ar emergindo após atravessar os dois blocos, como ilustra a figura.
Chamando de nar , npo e ncr aos índices de refração absolutos do ar, do polímero e do cristal,
respectivamente, a correta relação de ordem entre esses índices, de acordo com a figura, é:
a) nar  npo  ncr .
b) ncr  npo  nar .
c) ncr  nar  npo .
d) nar  ncr  npo .
e) npo  ncr  nar .
6. (Enem 2014) Uma proposta de dispositivo capaz de indicar a qualidade da gasolina vendida
em postos e, consequentemente, evitar fraudes, poderia utilizar o conceito de refração
luminosa. Nesse sentido, a gasolina não adulterada, na temperatura ambiente, apresenta razão
entre os senos dos raios incidente e refratado igual a 1,4. Desse modo, fazendo incidir o feixe
de luz proveniente do ar com um ângulo fixo e maior que zero, qualquer modificação no ângulo
do feixe refratado indicará adulteração no combustível.
Em uma fiscalização rotineira, o teste apresentou o valor de 1,9. Qual foi o comportamento do
raio refratado?
a) Mudou de sentido.
b) Sofreu reflexão total.
c) Atingiu o valor do ângulo limite.
d) Direcionou-se para a superfície de separação.
e) Aproximou-se da normal à superfície de separação.
www.nsaulasparticulares.com.br
Página 3 de 10
7. (Ufpr 2014) Um sistema de espelhos, esquematizado na figura abaixo, está imerso num
meio 1 cujo índice de refração é 2.
Um raio luminoso incide sobre o espelho horizontal pela trajetória a fazendo um ângulo de 𝟔𝟎º
em relação à reta normal deste espelho. Após esta reflexão, o raio segue a trajetória b e sofre
nova reflexão ao atingir outro espelho, que está inclinado de 75° em relação à horizontal. Em
seguida, o raio refletido segue a trajetória c e sofre refração ao passar deste meio para um
meio 2 cujo índice de refração é igual a 1, passando a seguir a trajetória d. Utilizando estas
informações, determine o ângulo de refração θ, em relação à reta normal da interface entre os
meios 1 e 2.
8. (Fmp 2014)
A figura acima ilustra um raio monocromático que se propaga no ar e incide sobre uma lâmina
de faces paralelas, delgada e de espessura d com ângulo de incidência igual a 60. O raio
sofre refração, se propaga no interior da lâmina e, em seguida, volta a se propagar no ar.
Se o índice de refração do ar é 1, então o índice de refração do material da lâmina é
a)
6
3
6
2
2
c)
2
d) 6
e) 3
b)
www.nsaulasparticulares.com.br
Página 4 de 10
9. (Ufg 2013) Um feixe de luz branca é empregado para transmitir sinais de telecomunicação.
Para isso, é instalada uma fibra óptica que possui índice de refração para o azul de 1,528 e
para o vermelho de 1,513. Considerando-se os raios de luz azul e vermelho e que a distância
entre duas cidades quaisquer é de 300 km, determine:
a) o raio de luz que chega primeiro. Justifique;
b) o atraso entre os raios ao percorrerem essa distância.
Dado: c = 3  108 m / s
10. (Ibmecrj 2013) Um raio de luz monocromática se propaga do meio A para o meio B, de tal
forma que o ângulo de refração β vale a metade do ângulo de incidência α . Se o índice de
refração do meio A vale 1 e o sen β  0,5 , o índice de refração do meio B vale:
a) 2
b) 3
c) 3
d) 0,75
e) 0,5
11. (Esc. Naval 2013) A figura abaixo mostra um prisma triangular ACB no fundo de um
aquário, contendo água, imersos no ar. O prisma e o aquário são feitos do mesmo material.
Considere que um raio luminoso penetra na água de modo que o raio retratado incida
perpendicularmente à face AB do prisma. Para que o raio incidente na face CB seja totalmente
refletido, o valor mínimo do índice de refração do prisma deve ser
Dados: nar  1,00; senθA  0,600 e senθB  0,800
a) 1,10
b) 1,15
c) 1,20
d) 1,25
e) 1,30
www.nsaulasparticulares.com.br
Página 5 de 10
Gabarito:
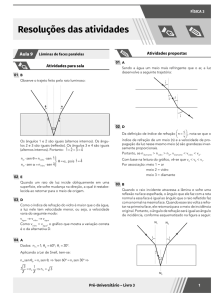
Resposta da questão 1:
[C]
A figura mostra o caminho seguido pelo feixe de laser.
tgr 
0,5

0,87
1
2  1  3
3
3
3
2
 r  30.
Aplicando a lei de Snell:
 1
nar sen θ  nág sen30  1 senθ  1,4    sen θ  0,7 
2
θ  45.
Resposta da questão 2:
[C]
As ondas estão passando do meio 1 (águas profundas) para o meio 2 (águas rasas). Esse é o
fenômeno da refração.
Resposta da questão 3:
[A]
Ao incidir radialmente sobre uma superfície circular o raio não sofre desvio,
independentemente do sentido de propagação. Ao sair para o ar, o raio está passando do meio
mais refringente para o menor refringente, afastando-se da normal.
Resposta da questão 4:
Aplicando a Lei de Snell, é possível encontrar o valor no ângulo θ2
n1  sen  θ1   n2  sen  θ2 
2
 2  sen  θ2 
2
1
sen  θ2  
2
θ2  30
1
www.nsaulasparticulares.com.br
Página 6 de 10
Com o valor deste ângulo, pela análise do triangulo destacado, é possível achar o valor da
distância D.
tg  θ2  
12
3 2

sen  θ2 
sen  θ2 

D2
2
D2
2
3 D 2

4
2
4
D
3
D
D
4 3
3
2,31mm
Resposta da questão 5:
[B]
Utilizando a Lei de Snell, tem-se que:
n  sen θ  cte.
Com isto, podemos analisar as refrações que acontecem na situação proposta.
[I] Refração na separação Ar-Polímero:
Se o feixe de luz aproxima-se da normal após a refração, o ângulo está diminuindo e
consequentemente sen θ também diminui. Logo, podemos concluir que npo  nar .
[II] Refração na separação polímero-cristal:
Como na situação anterior, a luz aproxima-se da normal após a refração. Logo, podemos
concluir que ncr  npo .
Assim, nem existe a necessidade de analisar a terceira refração, pois temos o resultado de que
ncr  npo  nar .
www.nsaulasparticulares.com.br
Página 7 de 10
Resposta da questão 6:
[E]
Como os ângulos de incidência e refração são definidos no intervalo de 0° a 90°, o menor
ângulo tem menor seno. Sendo fixo e não nulo o ângulo de incidência, apliquemos a lei de
Snell às duas situações, gasolina não adulterada e gasolina adulterada.
 sen i
 1,4

 sen r 1

 sen i  1,9
 sen r 2

 
sen i sen r 2 1,4


 0,74  sen r 2  0,74 sen r1 
sen r 1 sen i
1,9
sen r 2  sen r1 
r 2  r1.
Portanto o raio refratado no caso da gasolina adulterada é menor do que para a gasolina não
adulterada. Isso significa que o raio refratado aproximou-se da normal à superfície de
separação.
Resposta da questão 7:
A figura mostra os ângulos relevantes para a resolução da questão.
Aplicando a lei de Snell na refração:
n1 sen θ1  n2 sen θ2  2  sen 30°  1 sen θ 
2
1
2
 sen θ  sen θ 

2
2
θ  45.
www.nsaulasparticulares.com.br
Página 8 de 10
Resposta da questão 8:
[B]
A figura mostra os ângulos de incidência e refração:
Nessa figura:
d
tg r   1  r  45.
d
Aplicando a lei de Snell:
nar sen i  n L sen r  1 sen 60  n L sen 45 
nL 
3
2
 nL
2
2
 nL 
3
2

6
.
2
Resposta da questão 9:
Dados: naz  1,528; nvm  1,513; D  300 km  3  105 m / s; c  3  108 m / s.
a) O raio de luz que chega primeiro é o de maior velocidade.
Da definição de índice de refração absoluto:
c

v az  n
c
c 
az
n
 v
 nvm  naz  v vm  v az .

v
n 
c
v vm 

nvm

v vm  vaz  O raio de luz vermelho chega primeiro.
b) O atraso é dado pela diferença dos tempos de percurso:
D
D
D
D
D
t  taz  t vm  t 

 t 

 naz  nvm  
c
c
v az v vm
c
naz
nvm
t 
3  105
3  108
1,528  1,513 
 t  103  0,015   103  1,5  10 2 
t  1,5  105 s.
www.nsaulasparticulares.com.br
Página 9 de 10
Resposta da questão 10:
[C]
senβ  0,5  β  30
Como α  2β  α  60
Pela Lei de Snell, podemos escrever:
nA  senα  nB  senβ  1
3
1
 nB   nB  3 .
2
2
Resposta da questão 11:
[D]
O ângulo limite (L), neste caso, é θB conforme a figura abaixo:
Usando a Lei de Snell-Descartes para o ângulo limite:
sen L  sen θB  0,8
sen L 
nar
nprisma
Substituindo os valores:
1
0,8 
nprisma
nprisma  1,25
www.nsaulasparticulares.com.br
Página 10 de 10