Resoluções das atividades

FÍSICA 3
Resoluções das atividades
Aula 9
Atividades propostas
Lâminas de faces paralelas
01 A
Atividades para sala
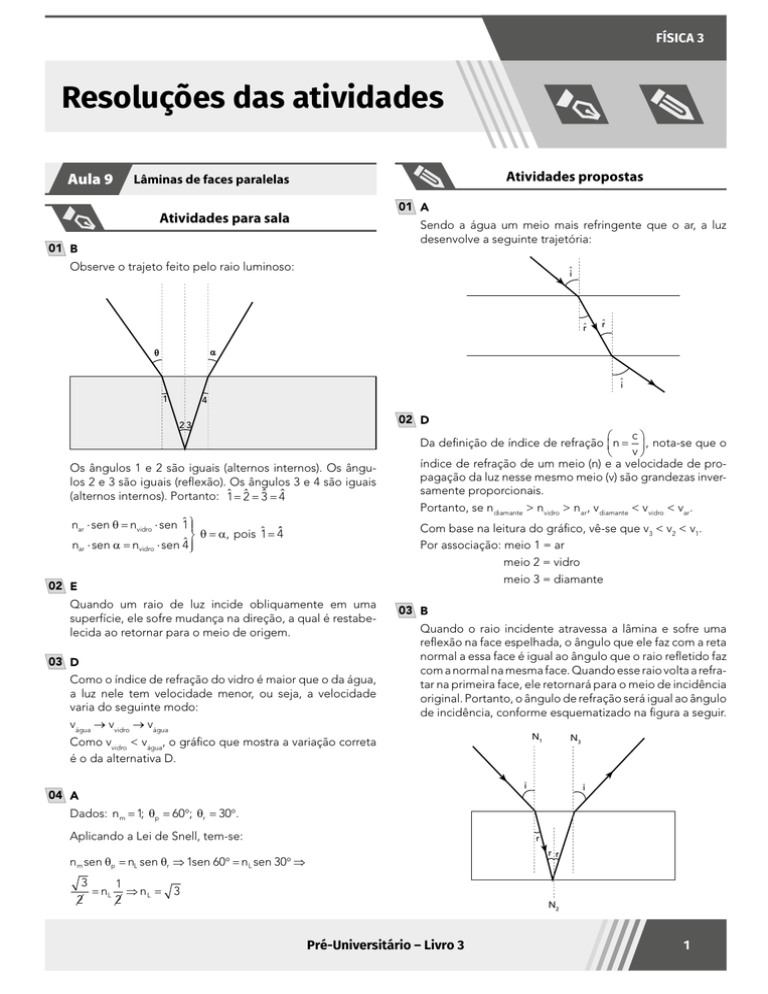
01 B
Sendo a água um meio mais refringente que o ar, a luz
desenvolve a seguinte trajetória:
Observe o trajeto feito pelo raio luminoso:
i
r
α
θ
1
4
02 D
c

Da definição de índice de refração  n =  , nota-se que o
v

índice de refração de um meio (n) e a velocidade de propagação da luz nesse mesmo meio (v) são grandezas inversamente proporcionais.
Portanto, se n diamante > n vidro > n ar , v diamante < v vidro < var.
Com base na leitura do gráfico, vê-se que v3 < v2 < v1.
Por associação: meio 1 = ar
meio 2 = vidro
meio 3 = diamante
Os ângulos 1 e 2 são iguais (alternos internos). Os ângulos 2 e 3 são iguais (reflexão). Os ângulos 3 e 4 são iguais
(alternos internos). Portanto: 1= 2= 3 = 4
nar ⋅ sen θ = nvidro ⋅ sen 1ˆ 
 θ = α, pois 1ˆ = 4̂ˆ
nar ⋅ sen α = nvidro ⋅ sen 4ˆ 
02 E
Quando um raio de luz incide obliquamente em uma
superfície, ele sofre mudança na direção, a qual é restabelecida ao retornar para o meio de origem.
03 B
03 D
Como o índice de refração do vidro é maior que o da água,
a luz nele tem velocidade menor, ou seja, a velocidade
varia do seguinte modo:
vágua → vvidro → vágua
i
23
Quando o raio incidente atravessa a lâmina e sofre uma
reflexão na face espelhada, o ângulo que ele faz com a reta
normal a essa face é igual ao ângulo que o raio refletido faz
com a normal na mesma face. Quando esse raio volta a refratar na primeira face, ele retornará para o meio de incidência
original. Portanto, o ângulo de refração será igual ao ângulo
de incidência, conforme esquematizado na figura a seguir.
N1
Como vvidro < vágua, o gráfico que mostra a variação correta
é o da alternativa D.
Dados: n m = 1; θp = 60°; θr = 30°.
Aplicando a Lei de Snell, tem-se:
3
i
r
r r
n m sen θp = nL sen θr ⇒ 1sen 60° = nL sen 30° ⇒
N3
i
04 A
3
1
= nL ⇒ n L =
2
2
r
Pré-Universitário – Livro 3
N2
1
FÍSICA 3
04 D
08 B
O fenômeno descrito na questão é chamado de continuidade óptica, uma vez que o índice de refração do vidro é
igual ao índice de refração do líquido. Desse modo, não há
refração do vidro para o líquido ou vice-versa. Analisando
as proposições, têm-se:
a) (F) A difícil distinção ocorre em virtude da continuidade óptica. Nesse fenômeno, o vidro e o líquido
parecem ser constituídos opticamente do mesmo
material.
b) (F) Conforme foi dito, não há refração entre o vidro e o
líquido.
c) (F) Como nesse caso não há refração, todas as características ondulatórias associadas à luz permanecem
constantes do vidro para o líquido ou vice-versa.
d)(V)
e) (F) A velocidade nos dois meios em questão é a mesma.
i = 60°
r
d
Utilizando a Lei de Snell, tem-se que n ⋅ sen θ = c ⋅ t ⋅ e.
Com isso, é possível analisar as refrações que ocorrem na
situação proposta.
I. Refração na separação ar-polímero:
Se o feixe de luz se aproxima da normal após a refração,
o ângulo está diminuindo e, consequentemente, o sen θ
também diminui. Logo, pode-se concluir que npo > n ar .
II. Refração na separação polímero-cristal:
Como na situação anterior, a luz aproxima-se da normal após a refração. Logo, conclui-se que ncr > npo.
Assim, nem há necessidade de analisar a terceira refração, pois conclui-se que n cr > n po > n ar .
d
05 B
A figura a seguir mostra os ângulos de incidência e refração.
Nessa figura, tem-se:
tg r =
d
= 1 ⇒ r = 45°.
d
Aplicando a Lei de Snell, tem-se:
nar sen ˆi = n L sen rˆ ⇒ 1 sen 60° = n L sen 45° ⇒
3
2
3
6
= nL
⇒ nL =
⇒ nL =
2
2
2
2
09 C
A luz que vem da parte do corpo das nadadoras que está
no ar sofre desvio ao entrar na água e não converge para
a câmera, principalmente porque a superfície da água está
agitada; com isso, verifica-se uma refração difusa.
10 D
06 D
Calculando o ângulo de refração:
nar ⋅ sen i = nv ⋅ sen r ⇒ 1⋅ sen 60° = 3 ⋅ sen r ⇒
3
1
= 3 ⋅ sen r ⇒ sen r = ⇒ r = 30°
2
2
Cada cor corresponde a uma frequência, e para cada uma
há um comprimento de onda específico, que por sua vez
tem um índice de refração correspondente. Dessa forma,
cada uma das cores sofrerá um deslocamento paralelo
particular.
Logo, o desvio lateral é dado por:
d=
d=
e ⋅ sen (i − r ) 2 ⋅ sen ( 60° − 30°)
=
cos 30°
cos r
2 ⋅ sen 30°
2
2 3
=
⇒d=
cm
3
3
3
2
07 B
Quando a imagem de um objeto real é observada por
meio de uma lâmina de faces paralelas, ela é vista direita
em relação ao objeto; dessa forma, caracteriza-se como
uma imagem virtual. Os conceitos desenvolvidos são os
mesmo aplicados no estudo das lentes esféricas.
2
Pré-Universitário – Livro 3