Semelhanças de triângulos

SEMELHANÇA DE TRIÂNGULOS
AS RESPOSTAS ESTÃO NO FINAL DOS EXERCÍCIOS.
Semelhança de triângulos
a)
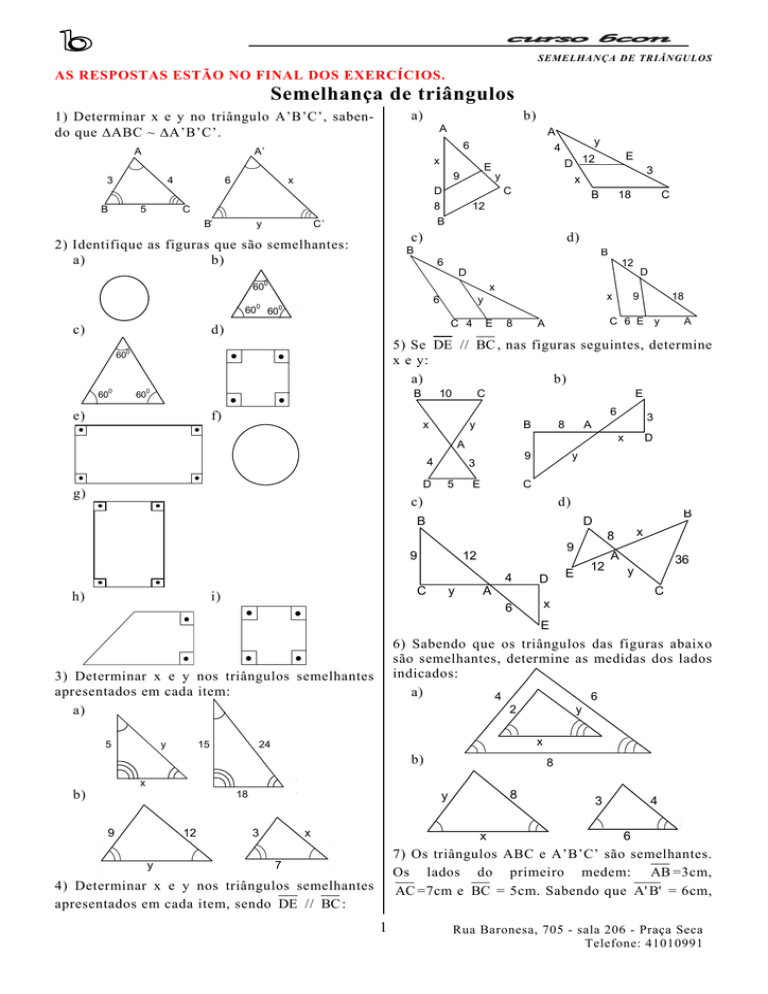
1) Determinar x e y no triângulo A’B’C’, sabendo que ΔABC ~ ΔA’B’C’.
A
b)
A
A
4
6
A’
x
3
4
B
5
6
9
x
D
8
B
C
B’
E
y
C’
y
y
C
3
18
C
12
c)
2) Identifique as figuras que são semelhantes:
a)
b)
E
D 12
x
B
d)
B
B
6
12
D
D
600
x
6
600 600
c)
C 4
d)
E
8
9
18
C 6 E y
A
A
5) Se DE // BC , nas figuras seguintes, determine
x e y:
a)
b)
600
600
x
y
600
B
e)
10
C
E
6
f)
x
y
B
8
x
A
4
D
g)
9
3
5
3
A
E
D
y
C
c)
d)
B
B
D
x
8
9
h)
12
C
i)
9
y
4
D
6
x
12
E
A
36
y
A
C
E
6) Sabendo que os triângulos das figuras abaixo
são semelhantes, determine as medidas dos lados
indicados:
a)
4
6
3) Determinar x e y nos triângulos semelhantes
apresentados em cada item:
a)
5
y
15
2
y
x
24
b)
8
x
b)
18
9
12
y
8
y
3
x
x
3
4
6
7) Os triângulos ABC e A’B’C’ são semelhantes.
Os lados do primeiro medem: AB =3cm,
AC =7cm e BC = 5cm. Sabendo que A' B' = 6cm,
7
4) Determinar x e y nos triângulos semelhantes
apresentados em cada item, sendo DE // BC :
1
Rua Baronesa, 705 - sala 206 - Praça Seca
Telefone: 41010991
SEMELHANÇA DE TRIÂNGULOS
A
determine a razão de semelhança e os outros dois
lados do Δ A’B’C’.
D
A’
A
E
B
B
C
B’
C
12) Na figura, os ângulos Rˆ e Ĉ são congruentes. Sendo AS = 3cm, SB = 6cm e BC = 15cm,
determine RS .
C’
8) Os triângulos ABC e A’B’C’, das figuras abaixo, são semelhantes. Calcule a razão de semelhança e as medidas dos elementos indicados:
a)
B
S
C’
A
A
R
5
y
24
26
13) Na figura, temos que: BE // CD , AB = 2( BC )
e BE = 14cm. Calcule CD .
B
13
C
C
D
A’
x
B’
E
b)
B
B’
C
8
y
x
C
6
A’
A
8
B x
b)
6
30
A
3
C
b)
x
x
E
x
B
y
D 18
6
D
y
5
C’
A
9) Calcule x e y:
a)
4
3
A
14) Nas figuras seguintes, DE // BC , determine
x:
a)
c)
0
60
B
C
7
d)
A
9
15
12
D
4
B
20
15
c)
8
10
x
x
E
D 4
5x -1
E
5
B
x+1
C
C
3
10)
Se
BE // CD ,
AD =15cm,
AC =9cm,
CD =12cm e AE = 5cm, determine AB e BE .
C
D
B
A
16
15) Os triângulos ABC e A’B’C’ são semelhantes. Determine x e y:
A’
a) A
12
y
6
21
E
x
B
9
y
C
B’
C’
21
b)
A
E
A’
15
x
B
A
y
3
B’
C
5
C’
4
11) Na figura, determine os valores de x e y,
sendo DE // BC , AD = x, AE =6cm, DB =2cm,
EC =3cm, DE = 8cm e BC = y.
2
Rua Baronesa, 705 - sala 206 - Praça Seca
Telefone: 41010991
SEMELHANÇA DE TRIÂNGULOS
c)
A
A’
A
9
5
x
8
24
B
7
C
B’
D
3
B
C’
y
16) Os triângulos ABC e ADE são semelhantes,
sendo DE // BC . Determine x e y:
a)
c)
B
y
12
x
D
E
7
C
12
x
B
18
D
36
24
C
b)
9
E
y
B 8 D
12
A
8
E
D
4
B
14
21
y
21
C
C
10
x
A
y
E
8
C
4
4
3
C’
8
x
9
4
C
y
3
x
3
B’
B
4
y
22) Determine x nas figuras:
a)
b)
A’
x
x
x
21) Determine a altura de um prédio cuja sombra
mede 40m, enquanto um mastro de 6m de altura,
no mesmo instante, tem uma sombra de 10m.
17) Os triângulos ABC e A’B’C’ são semelhantes. Determine x:
a)
A
4
4
20) Em determinado momento, uma torre projeta
uma sombra de 32m e um poste de 3m de altura
projeta uma sombra de 8m. Determine a altura da
torre.
d)
A
6
E
19) A razão de semelhança de dois triângulos é
4
. Sabendo que os lados do maior triângulo me5
dem, respectivamente, 10cm, 15cm e 20cm, calcule o comprimento dos lados homólogos do triângulo menor.
A
10
5
3
c)
b)
A’
A
x
4
x
12
B
5
C
6
3
B’
C’
8
23) Na figura abaixo, Ĉ ≡ Eˆ , BC =2cm,
AB =4cm, DE = 6cm e AE = 9cm. Calcule AC e
AD .
c)
B
B’
C
15
25
A’
C
9
x
B
C’
A
D
A
E
18) Sendo que os triângulos ABC e ADE são semelhantes, determine x e y:
a)
b)
24) Determine x e y nas figuras:
a)
6
x
8
y
6
4
x
6
4
8
18
y
4
y
6
10
15
x
c)
d)
3
Rua Baronesa, 705 - sala 206 - Praça Seca
Telefone: 41010991
SEMELHANÇA DE TRIÂNGULOS
A
b)
y
3
E
4
x
5
6
B
25) Qual é a altura de um prédio cuja sombra tem
15m enquanto uma vara de 6m colocada em pé
tem uma sombra de 2m?
28) Na figura abaixo, sabe-se que Ŝ ≡ B̂ ,
AR =7cm, AS =5cm, SR =4cm e AB =10cm. Determine AC e BC .
26) Na figura, ABCD é um paralelogramo, os ângulos E e F são retos, os lados do paralelogramo
medem
e
AB =30cm.
Sendo
BC =10cm
DF =24cm, determine DE .
D
C
D
A
S
R
C
B
C
F
A
E
B
27) Na figura, o Δ ABC é retângulo em A e o
Δ DEC é retângulo em D. Se que AB = 8cm, AC
= 15cm, BC = 17cm e CD = 5cm, determine
DE .
Respostas
1) x = 8 e y = 10
2) a e f; b e d;
c e i; e e g
3) a) x = 6 e y = 8
b) x = 4 e y = 21
4) a) x = 24 e y = 2
b) x = 2 e y = 6
c) x = 12 e y = 4
d) x = 15 e y = 9
5) a) x = 6 e y = 8
8
e y =18
3
9
c) x = e y = 8
2
d) x = 48 e y = 32
b) x =
6) a) x = 4 e y = 3
b) x =12 e y = 6
7)
14) a) 4
b) 15
c) 6
d) 5
15) a) x = 4 e y = 7
b) x = 9 e y = 12
c) x = 27 e y = 21
16) a) x = 5 e y =14
b) x = 14 e y = 6
c) x = 32 e y = 27
d) x = 16 e y = 20
17) a) 6 b) 10 c) 15
1
; 10cm e 14cm
2
8) a)
1
; x = 10 e
2
y = 12
b) 2; x = 4 e y= 60 0
9) a) x = 3 e y = 25
b) x = 4 e y = 3
c) x =12 e y = 20
10) x = 3cm e y = 4cm
18) a) x = 5 e y = 4
b) x = 27 e y = 32
31
32
11) x = 4cm e y = 12cm
c) x =
e y=
3
3
12) 5cm
d) x = 7 e y = 8
13) 21cm
4
19) 8cm, 12cm, 16cm
20) 12m
21) 24m
22) a) 12 b) 6 c) 6
23) AC = 3 e AD = 12
24) a) x = 2 e y = 3
b) x = 8 e y = 10
25) 45m
26) 8cm
27)
8
3
28) AC = 14 e BC = 8
Rua Baronesa, 705 - sala 206 - Praça Seca
Telefone: 41010991