Cisalhamento transversal

Capítulo 7:
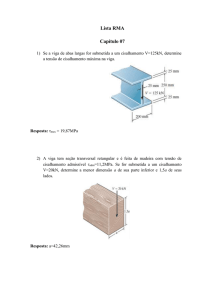
Cisalhamento
transversal
Adaptado pela prof. Dra. Danielle Bond
Cisalhamento em elementos retos
• Vimos que por conta dos
carregamentos aplicados, as
vigas desenvolvem uma
força
de
cisalhamento
interna (força cortante) e
momento fletor que variam
de ponto para ponto ao
longo do eixo da viga.
• O cisalhamento V é o
resultado
de
uma
distribuição de tensão de
cisalhamento transversal que
age na S.T. da viga. As
tensões de cisalhamento
longitudinais também agirão
na viga.
Cisalhamento em elementos retos
•
É possível explicar fisicamente por que a tensão de cisalhamento se
desenvolve nos planos longitudinais de uma viga considerando que ela é
composta por 3 tábuas.
SOLTAS: Deslizam
uma sobre a outra
UNIDAS: As tensões
longitudinais entre elas
impedirão que uma
deslize sobre a outra
Cisalhamento em elementos retos
•
Quando é aplicado um cisalhamento V, as linhas de grade tendem a se
deformar conforme a fig.
•
Essa distribuição não uniforme por cisalhamento fará com que ela se
deforme e não permaneça plana, (é desprezada da viga esbelta).
•
Desenvolveremos uma fórmula para a tensão de cisalhamente
indiretamente, isto é, usando a fórmula da flexão e a relação entre o
momento fletor e cisalhamento , ou seja:
V  dM dx
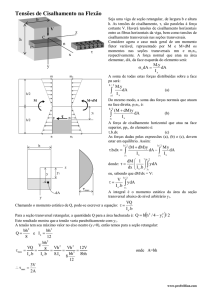
A fórmula do cisalhamento
• É determinada a partir do estudo da tensão de cisalhamento longitudinal e
nos resultados da eq. : V  dM dx
•Para mostrar como essa relação é definida, consideraremos o equilíbrio das
forças horizontais da figura abaixo:
A fórmula do cisalhamento
Elemento retirado da viga:
Diagrama de corpo livre:
A fórmula do cisalhamento
•Considerando segmento na parte superior
secionado em y’ em relação ao eixo neutro:
do
elemento
do
elemento
A fórmula do cisalhamento
•Considerando segmento na parte superior
secionado em y’ em relação ao eixo neutro:
 
My
I
A fórmula do cisalhamento
V  dM dx
V  dM dx
A integral representa o momento de primeira ordem da área A`em torno do eixo
neutro que será representado pelo símbolo Q.
Visto que a localização do centróide da área A`é determinada por
A fórmula do cisalhamento

VQ
It
onde Q   ydA  y ' A'
A'
τ = tensão de cisalhamento no elemento no ponto
localizado à distância y`do eixo neutro
V = força de cisalhamento interna resultante
I = momento de inércia da área da S.T. inteira
t = largura da área da seção transversal do elemento,
medida no ponto onde a τ deve ser considerada
A’ = é a porção superior da área da ST do elemento
y' = é a distância do centróide da área (A`)
considerada até a linha neutra.
Tensões de cisalhamento em vigas
Seção transversal retangular
• Para uma viga com seção
transversal retangular, a
tensão de cisalhamento
varia parabolicamente
com a altura. A tensão de
cisalhamento máxima
ocorre ao longo do eixo
neutro.
Tensões de cisalhamento em vigas
Viga de abas largas
Tensões de cisalhamento em vigas
Viga de abas largas
• Ela consiste em 2 abas (largas) e uma “alma”. Ocorre um salto na tensão de
cisalhamento na junção aba-alma, visto que a espessura da seção transversal
muda nesse ponto (t na fórmula do cisalhamento muda)
Exemplo 7.1
A viga é feita de madeira e está sujeita a uma força de
cisalhamento vertical interna resultante V = 3 kN. (a) Determine
a tensão de cisalhamento na viga no ponto P e (b) calcule a
tensão de cisalhamento máxima na viga.
Exemplo 7.1
Exemplo 7.1
Exemplo 7.2
Uma viga T de aço tem as dimensões mostradas na Fig. Se for
submetida a uma força de cisalhamento V=80kN, a)trace uma
curva da distribuição da tensão de cisalhamento que age da
seção trasnversal da viga e b) determine a força de cisalhamento
à qual a alma resiste.
Exemplo 7.2
Exemplo 7.2
Exemplo 7.3
A viga mostrada na figura é feita com duas tábuas. Determine a
tensão de cisalhamento máxima necessária na cola para que ela
mantenha as tábuas unidas ao longo da linha de junção. Os
apoios em B e C exercem apenas reações verticais na viga.
Exemplo 7.3