Flexão - tensão de cisalhamento - 303 kB

Tensões de Cisalhamento na Flexão
b
V
z
C
h
n
m

x
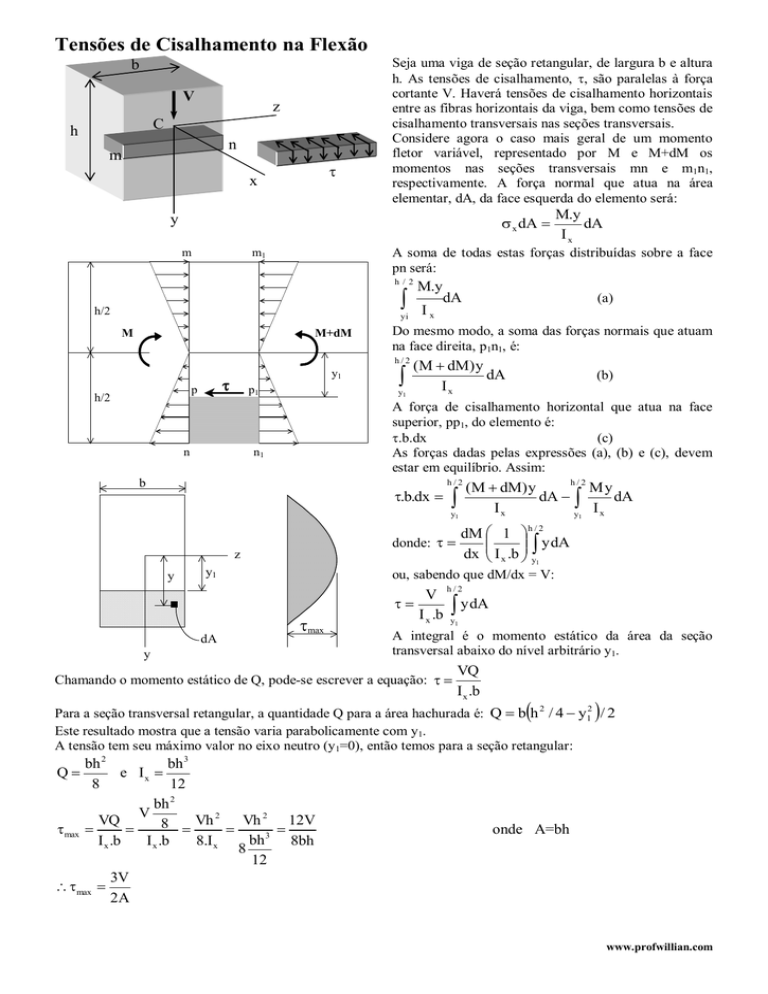
Seja uma viga de seção retangular, de largura b e altura
h. As tensões de cisalhamento, , são paralelas à força
cortante V. Haverá tensões de cisalhamento horizontais
entre as fibras horizontais da viga, bem como tensões de
cisalhamento transversais nas seções transversais.
Considere agora o caso mais geral de um momento
fletor variável, representado por M e M+dM os
momentos nas seções transversais mn e m1n1,
respectivamente. A força normal que atua na área
elementar, dA, da face esquerda do elemento será:
 x dA 
y
m
A soma de todas estas forças distribuídas sobre a face
pn será:
m1
h/2

h/2
M+dM

p
h/2
p1

y1
n1
b
(M  dM) y
dA
Ix
h/2
.b.dx 

y1
y1
(M  dM) y
My
dA  
dA
Ix
Ix
y1
h/2
ou, sabendo que dM/dx = V:

dA
(b)
h/2
dM  1 

  ydA
dx  I x .b  y1
donde:  
z
y
(a)
A força de cisalhamento horizontal que atua na face
superior, pp1, do elemento é:
.b.dx
(c)
As forças dadas pelas expressões (a), (b) e (c), devem
estar em equilíbrio. Assim:
dx
n
dA
Do mesmo modo, a soma das forças normais que atuam
na face direita, p1n1, é:
h/2
y1
M.y
Ix
yi
M
M.y
dA
Ix
max
y
V
I x .b
h/2
 ydA
y1
A integral é o momento estático da área da seção
transversal abaixo do nível arbitrário y1.
Chamando o momento estático de Q, pode-se escrever a equação:  
VQ
I x .b


Para a seção transversal retangular, a quantidade Q para a área hachurada é: Q  b h 2 / 4  y12 / 2
Este resultado mostra que a tensão varia parabolicamente com y1.
A tensão tem seu máximo valor no eixo neutro (y1=0), então temos para a seção retangular:
bh 2
bh 3
e Ix 
8
12
bh 2
V
2
2
VQ
8  Vh  Vh  12V
max 

bh 3 8bh
I x .b
I x .b
8.I x
8
12
3V
 max 
2A
Q
onde A=bh
www.profwillian.com
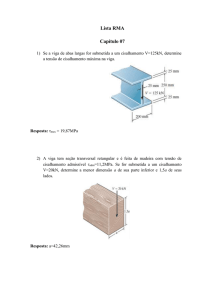
1) Para a seção transversal “T” de uma viga, vista na figura ao lado,
calcule:
a) Momento de inércia (em relação ao eixo neutro da seção);
b) a tensão máxima normal,  em MPa, para um fletor de 55,5 kN.m
c) a tensão máxima de cisalhamento , , para um cortante de 40,4 kN
Solução:
Centro de gravidade da seção “T” (em relação à base)
y
 A.y  (6 16)  8  (16  6) 19  13,5 cm
(6  16)  (16  6)
A
a) Momento de inércia para a seção “T”
 6 163
  16  63

I   IC  A.d 2  
 6 16  (13,5  8)2   
 16  6  (19  13,5)2   8144 cm 4
 12
  12

b) Tensão máxima normal:
5550000

 13,5  9200 N / cm 2  92 MPa
8144
Momento Estático Q (abaixo da linha neutra):
13,5
Q   A.y  (6  13,5) 
 546,75 cm 3
2
c) Tensão máxima de cisalhamento:
V Q 40400  546,75


 452 N / cm 2  4,52 MPa
Ib
8144  6
2) Para a seção transversal “I” da viga vista na figura ao lado,
calcule: o momento de inércia (em relação ao eixo neutro da seção)
e a tensão máxima normal, , para um fletor de 66 kN.m e a tensão
máxima de cisalhamento , , para um cortante de 44 kN
Solução:
a) Momento de inércia para a seção “I”
 42  63

6  503
I   IC  A.d 2  
 42  6  282   2 
 459148 cm 4
12
 12

b) Tensão máxima normal:
6600

 31  0,4456 kN / cm 2  4,456 MPa
459148
Momento Estático Q (abaixo da linha neutra):
25
Q   A.y  (6  25)   (42  6)  28  8931 cm 3
2
c) Tensão máxima de cisalhamento:
VQ
44  8931


 0,1426 kN / cm 2  1,426 MPa
Ib
459148  6
www.profwillian.com
7.5 Se a viga T for submetida a um cisalhamento vertical V = 10 kip, qual
será a tensão de cisalhamento máxima nela desenvolvida? Calcular também o
salto da tensão de cisalhamento na junção aba-alma AB. Desenhar a variação
de intensidade da tensão de cisalhamento em toda a seção transversal. Mostrar
que IEN=532,04 pol4.
7.15 Determinar a tensão de cisalhamento máxima no eixo com seção
transversal circular de raio r e sujeito à força cortante V. Expressar a resposta
em termos da área A da seção transversal.
www.profwillian.com
7.17 Determinar as maiores forças P nas extremidades que o elemento pode
suportar, supondo que a tensão de cisalhamento admissível seja adm = 10 ksi.
Os apoios em A e B exercem apenas reações verticais sobre a viga.
7.21 Os apoios em A e B exercem reações verticais sobre a viga de madeira.
Supondo que a tensão de cisalhamento admissível seja adm = 400 psi,
determinar a intensidade da maior carga distribuída w que pode ser aplicada
sobre a viga.
www.profwillian.com