Solução

www.fisicaexe.com.br
De um ponto de uma circunferência de raio 2 m partem simultaneamente dois móveis
que percorrem esta circunferência no mesmo sentido com velocidades que estão entre si na
razão de 2/5,. Sabendo-se que os móveis se encontram cada 10 s determinar sua acelerações
centrípetas.
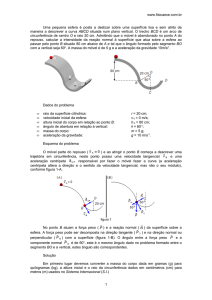
Esquema do problema
Adota-se como origem do espaço o ponto de onde partem
os móveis, assim suas posições iniciais serão  0 1 =  0 2 = 0, e com
orientação positiva no sentido contra-relógio. As acelerações
centrípetas dos móveis apontam para o centro da circunferência,
elas são responsáveis por fazer os móveis percorrem a curva, mas
não alteram a velocidade escalar que é tangente à circunferência.
Dados do problema
figura 1

raio da circunferência (trajetória):

razão das velocidades dos móveis:

intervalo de tempo entre os encontros:
R = 2 m;
v1 2
 ;
v2 5
 t = 10 s.
Solução
Da razão entre as velocidades dada no problema podemos escrever
v1 
2
v2
5
(I)
A aceleração centrípeta é dada por
a CP 
v2
R
escrevendo esta expressão para os dois móveis, temos
a CP1 
v 12
R
e
a CP 2 
v 22
R
(II)
Como os móveis estão em Movimento Circular Uniforme (M.C.U.) a expressão que
rege este movimento é
  0   t
escrevemos as equações deste movimento para os móveis, obtemos
 1   01   1 t
 2   02   2 t
 1  0  1 t
2  0  2 t
1  1 t
2  2 t
lembrando que a velocidade escalar e a velocidade angular estão relacionadas pela fórmula
1
www.fisicaexe.com.br
v R
v

R
podemos substituir este valor nas expressões acima
1 
v1
R
t
2 
e
v2
R
t
(III)
Para o primeiro encontro dos móveis devemos ter a condição
 2  1  2
substituindo as expressões de (III) nesta condição, temos
v2
R
v1
t
R
t  2
substituindo o intervalo de tempo para o primeiro encontro e o raio da circunferência, dado no
problema, e a expressão (I), ficamos com
v2
2
1 2

 v 2  10  2 
25

5v 2  2v 2  2 
10 
3v 2  2 
v2 
2
 m/s
3
(IV)
Substituindo este valor na expressão (II) para a aceleração centrípeta do móvel 2,
temos um dos resultados
a CP 2 
a CP 2
a CP 2 
12 
 
23 
1 4
 . 2
2 9
2 2
 m/s
9
2
2
Substituindo a expressão (I) na expressão (II) para a aceleração centrípeta do móvel 1
1 2

 v2 
25

1 4 2
a CP1 
v
2 25 2
2 2
a CP1 
v
25 2
2
a CP1 
substituindo a velocidade do móvel 2 encontrada em (IV), temos o outro resultado
a CP1 
2 2 
 
25  3 
2
2
www.fisicaexe.com.br
a CP1 
a CP1 
2 4 2

25 9
8
 2 m/s 2
225
3