Física - Mecânica Clássica

www.fisicaexe.com.br
Um móvel em Movimento Uniformemente Variado (M.U.V.) percorre uma circunferência
de raio 5 m com aceleração escalar constante e igual a 4 m/s 2 . Admitindo que no instante
t = 0 o móvel esteja a 10 m da origem dos espaços (medido sobre a circunferência) e a sua
velocidade seja de 15 m/s , determinar:
a) A equação horária do movimento sob a forma linear e angular;
b) A equação da velocidade sob a forma linear e angular;
c) A velocidade angular do móvel no instante t = 10 s ;
d) As acelerações centrípeta e total no instante t = 2 s .
Dados do problema




R=3m;
S 0 = 10 m ;
v 0 = 15 m/s ;
2
a = 4 m/s .
raio da circunferência (trajetória):
espaço inicial do móvel:
velocidade inicial do móvel:
aceleração do móvel:
Esquema do problema
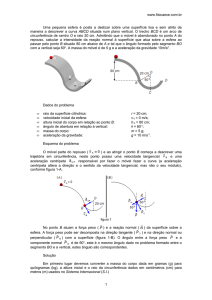
Adota-se um referencial com origem (O)
orientado positivamente no sentido contra-relógio, a
partir do qual se medem a posição inicial ( S 0 ) e a
posição angular inicial ( ϕ 0 ) do móvel (figura 1).
Solução
a) A equação de movimento na forma linear é
S = S 0+v 0 t +
a 2
t
2
figura 1
substituindo diretamente os dados do problemas, temos
4 2
t
2
S = 10+15t+
S = 10+15t+ 2t
2
Usando as expressões que relacionam as grandezas escalares e angulares
S = ϕR
v = ωR
a = γR
podemos obter o espaço angular inicial, a velocidade angular inicial e a aceleração angular
S 0 = ϕ0R
S0
ϕ0 =
R
10
ϕ0 =
5
ϕ 0 = 2 rad
v 0 = ω0R
v0
ω0 =
R
15
ω0 =
5
ω 0 = 3 rad/s
a = γR
a
γ0=
R
4
γ0=
5
2
γ 0 = 0,8 rad/s
A equação de movimento na forma angular é
ϕ = ϕ 0 +ω 0 t +
substituindo os valores acima, obtemos
1
γ 2
t
2
www.fisicaexe.com.br
ϕ = 2+3t +
0,8 2
t
2
ϕ = 2+3t +0,4 t
2
b) A equação da velocidade na forma linear é
v = v 0 +a t
substituindo diretamente os dados do problemas, temos
v = 15+4 t
A equação de movimento na forma angular é
ω = ω 0 +γ t
substituindo os valores do item anterior, obtemos
ω = 3+0,8 t
c) Usando a expressão do item anterior para a velocidade angular em t = 10 s , temos
ω = 3+0,8 .10
ω = 3+8
ω = 11 rad/s
d) Em cada ponto da circunferência o móvel
possui uma aceleração tangente à curva
(aceleração de módulo a = 4 m/s 2 dada no
problema), uma aceleração centrípeta ( a cp )
na direção radial com sentido apontado para o
centro da circunferência e a aceleração total
( a t ) representada pela soma vetorial das
outra duas partes (figura 2).
A aceleração escalar é constante em
todos os instantes da trajetória (vide
enunciado).
A aceleração centrípeta é dada por
figura 2
2
a cp =
v
R
Para encontrarmos a aceleração centrípeta em t = 2 s devemos ter a velocidade
neste instante usando a expressão para a velocidade escalar encontrada no item (b)
v = 15+4 .2
v = 15+8
v = 23 m/s
substituindo este valor
temos
e o raio da circunferência na expressão da aceleração centrípeta,
2
www.fisicaexe.com.br
2
23
5
529
a cp =
5
a cp =
a cp = 105,8 m/s
2
Usando o Teorema de Pitágoras temos a aceleração total (figura 2)
2
2
2
a t = a +a cp
a 2t = 4 2+105,8 2
2
a t = 16+11193,64
a 2t = 11 209,64
a t = √ 11209,64
a cp = 105,87 m/s
3
2