Problemas de análise de circuitos com

UNIVERSIDADE NOVA DE LISBOA
FACULDADE DE CIÊNCIAS E TECNOLOGIA
ELECTRÓNICA PARA AS ENGENHARIAS BIOMÉDICA E FÍSICA
Problemas de análise de circuitos com Amplificadores-Operacionais
Série elaborada pelo monitor Bruno Esperança
Amplificadores-Operacionais
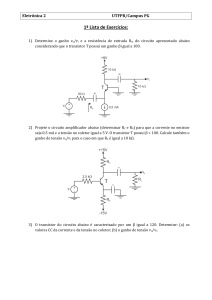
Problema 1
Assumindo amplificadores-operacionais ideais determine o ganho de tensão vo vi e a
resistência de entrada Rin para cada um dos seguintes circuitos:
100 kΩ
100 kΩ
10 kΩ
10 kΩ
-
vi
-
vi
vo
vo
+
+
10 kΩ
a)
b)
100 kΩ
100 kΩ
10 kΩ
10 kΩ
-
vi
-
vi
vo
10 kΩ
vo
+
+
10 kΩ
c)
d)
100 kΩ
10 kΩ
vi
-
vi
-
vo
+
e)
vo
+
f)
Problema 2
Desenhe uma montagem inversora para a qual o ganho de tensão é de − 4 V / V e a
resistência total utilizada é 100 kΩ .
Amplificadores-Operacionais
Problema 3
Considere o seguinte circuito:
Desenhe um amplificador com um ganho de tensão de − 50 V / V com a maior
resistência de entrada possível usando apenas resistências inferiores a 10 MΩ . Qual a
resistência de entrada do circuito que dimensionou?
Problema 4
Considere que as resistências do circuito do problema anterior são fabricadas com x%
de tolerância. Qual a tolerância no ganho em malha fechada resultante?
Assuma que o amplificador-operacional é ideal. Se o ganho nominal de tensão é de
− 100 V / V e x = 5 determine o intervalo de valores esperados para o ganho do
circuito.
Problema 5
Desenhe um circuito baseado na montagem não-inversora com um ganho de + 1.5 V / V
usando apenas resistências de 10 kΩ . Note que há duas topologias possíveis. Qual
destas pode ser facilmente convertida para se obter um ganho de + 1.0 V / V ou
+ 2.0 V / V simplesmente curto-circuitando uma resistência em cada caso?
Amplificadores-Operacionais
Problema 6
Considere o seguinte circuito:
Use a sobreposição para determinar vo em função de v1 e v2.
Determine a expressão da tensão de saída para as seguintes tensões de entrada:
v1 = 10 sin (2π × 60t ) − 0.1sin (2π × 1000t ) [V ]
v 2 = 10 sin (2π × 60t ) + 0.1sin (2π × 1000t ) [V ]
Problema 7
Considere a montagem diferencial:
Assuma que R = 100 kΩ + x kΩ . Determine uma expressão do ganho em modo comum
resultante para o pior caso.
Calcule o ganho em modo comum resultante para o pior caso quando x = 0.1, 1 e 5 .