UNIP – 8P/7W- 01 - EE/EN – Eletrônica Aplicada

UNIP – 8P/7W- 01 - EE/EN – Eletrônica Aplicada – 2.a Prova Sem Consulta e permitido o uso de calculadora.
/11/2010 - Tempo 80min – Turma B
NOME........................................................................ N.o ....................................................... Nota...............
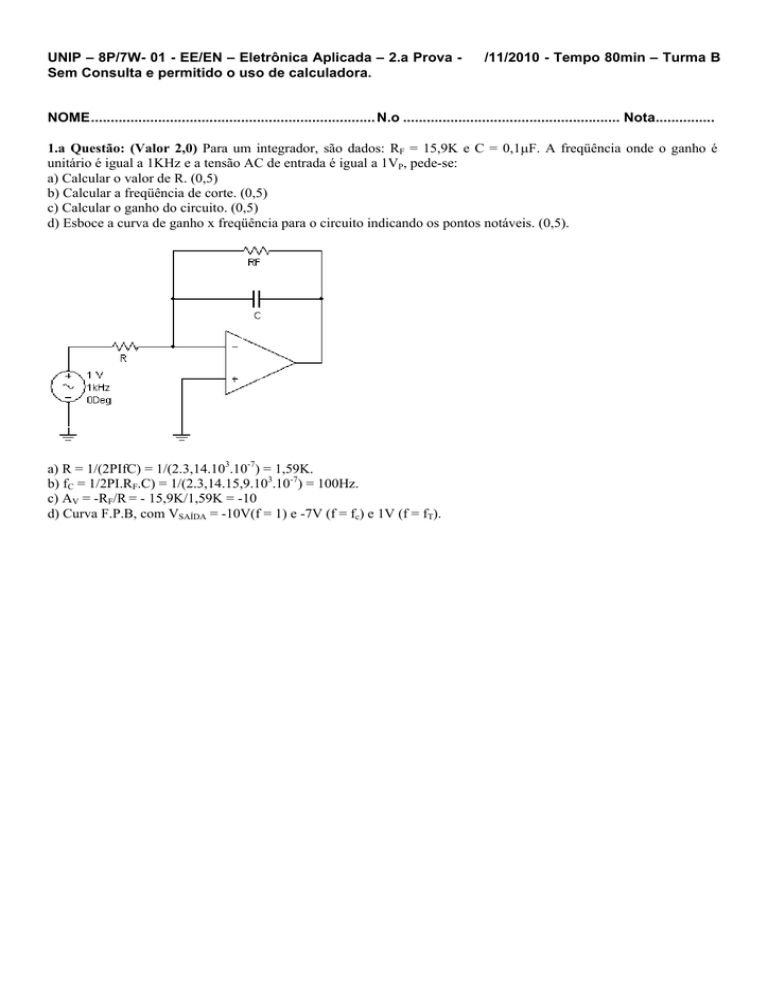
1.a Questão: (Valor 2,0) Para um integrador, são dados: RF = 15,9K e C = 0,1µF. A freqüência onde o ganho é
unitário é igual a 1KHz e a tensão AC de entrada é igual a 1VP, pede-se:
a) Calcular o valor de R. (0,5)
b) Calcular a freqüência de corte. (0,5)
c) Calcular o ganho do circuito. (0,5)
d) Esboce a curva de ganho x freqüência para o circuito indicando os pontos notáveis. (0,5).
a) R = 1/(2PIfC) = 1/(2.3,14.103.10-7) = 1,59K.
b) fC = 1/2PI.RF.C) = 1/(2.3,14.15,9.103.10-7) = 100Hz.
c) AV = -RF/R = - 15,9K/1,59K = -10
d) Curva F.P.B, com VSAÍDA = -10V(f = 1) e -7V (f = fc) e 1V (f = fT).
2.a Questão: (Valor 1,5) Um comparador de amplitude é alimentado com uma única tensão de +12V (amplitude
máxima de saída). Pede-se:
a) A tensão de disparo e retorno. (0,5)
b) A tensão de histerese. (0,5)
c) Um gráfico de transferência entrada e saída. (0,5)
a) UTH = 12. 10K/20K = 6V e UTL = 0
b) VH = 6V
c) Curva de transferência saída x entrada com os valores acima.
3.a Questão: (Valor 2,0) A equação de um oscilador é descrita pela taxa de realimentação. Pede-se:
a) A expressão da freqüência do circuito em rad/s. (1,0)
b) O ganho mínimo do circuito para que haja oscilação do circuito. (1,0)
β=
R3
(R 3 − 5RX C2 ) + j(X3C − 6R 2 X C )
a) A parte imaginária igual a zero => XC3 – 6R2XC = 0 => XC2 = 6R2 e XC = 1/Wc => w = 1/(√6 RC).
b) Somente a parte real de β = R3/(R3 – 30R3) = - 1/29 => Aβ = 1 => AMIN = -29.
4.a Questão : (Valor 1,5) Para o circuito a seguir :
a) Escreva a expressão para a saída V0. (1,0).
b) Calcular o valor médio e eficaz total da tensão de saída V0 para o item a. (0,5).
a) V0 = 5 cos500t - sen500t + 10.
b) V0DC = 10V e VORMS = √((5/√2)2 + (1/√2)2 + 102) = 10,63V.
1.a Questão: (Valor 2,0) Para um integrador, são dados: RF = 15,9K e C = 0,1µF. A freqüência onde o ganho é
unitário é igual a 10KHz e a tensão AC de entrada é igual a 100mVP, pede-se:
a) O valor de R. (0,5)
b) Calcular a freqüência de corte. (0,5)
c) Calcular o ganho do circuito. (0,5)
d) Esboce a curva de ganho x freqüência para o circuito indicando os pontos notáveis. (0,5).
a) R = 1/(2PIfC) = 1/(2.3,14.103.10-7) = 159.
b) fC = 1/2PI.RF.C) = 1/(2.3,14.15,9.103.10-7) = 100Hz.
c) AV = -RF/R = - 15,9K/1,59K = -100
d) Curva F.P.B com os valores A = -10V (f = 1), A = -7V (f = fC) e A = -1 (f = fT)
2.a Questão: (Valor 1,5) Um comparador de amplitude é alimentado com uma única tensão de +10V (amplitude
máxima de saída). Pede-se:
a) A tensão de disparo e retorno. (0,5)
b) A tensão de histerese. (0,5)
c) Um gráfico de transferência entrada e saída. (0,5)
a) UTH = 12. 10K/20K = 5V e UTL = 0
b) VH = 5V
c) Curva de transferência saída x entrada com os valores acima.
3.a Questão: (Valor 2,0) A equação de um oscilador é descrita pela taxa de realimentação. Pede-se:
a) A expressão da freqüência do circuito em rad/s. (1,0)
b) O ganho mínimo do circuito para que haja oscilação do circuito. (1,0)
β=
R3
(R 3 − 5RX C2 ) + j(X3C − 6R 2 X C )
a) A parte imaginária igual a zero => XC3 – 6R2XC = 0 => XC2 = 6R2 e XC = 1/Wc => w = 1/(√6 RC).
b) Somente a parte real de β = R3/(R3 – 30R3) = - 1/29 => Aβ = 1 => AMIN = -29.
4.a Questão : (Valor 1,5) Para o circuito a seguir :
a) Escreva a expressão para a saída V0. (1,0).
b) Calcular o valor médio e eficaz total da tensão de saída V0 para o item a. (0,5).
a) V0 = -5 sen500t + cos500t + 10.
b) V0DC = 10V e VORMS = √((5/√2)2 + (1/√2)2 + 102) = 10,63V.