Centro Educacional Sesc Cidadania
Ensino Fundamental Anos Finais
Goiânia, ____/____/2017.
8º ano
Turma: _____
nº ___
Nome do (a) Aluno (a): ________________________________________________
Professor(a): Victor Arraes
Atividade do 1º trimestre - Disciplina: Geometria
.Noções e Proposições Primitivas
.Segmento de Reta
.Ângulos
Q01: Leia atentamente o pequeno texto a seguir.
A forma organizada e lógica de ver a Geometria deve-se ao
matemático grego Euclides.
Ele reuniu em uma obra de 13 volumes, chamada Os Elementos
( ), todos os estudos de Geometria até então
conhecidos, organizando-os e sistematizando-os logicamente. Há
Euclides ( 330 a.C. - 260
a. C. )
poucas informações sobre a vida de Euclides. Sabe-se que foi
chamado para ensinar Matemática na escola criada por Ptolomeu, mais conhecida como “Museu”, onde se
tornou o primeiro diretor. Conta-se que um dia o rei lhe perguntou se não existia um método mais simples
para aprender Geometria e que Euclides respondeu: “Não existem estradas reais para se chegar a
Geometria”.
Euclides é conhecido como um dos matemáticos mais importantes da Grécia
Clássica e de todos os tempos.
Marque a alternativa a seguir que contém a afirmativa CORRETA que explica a frase dita por Euclides ao
rei, destacada no texto acima.
a) Os pontos de partida para explicar a Geometria são números que não pertencem ao conjunto dos
Reais.
b) A base da Geometria, segundo Euclides, são conceitos intuitivos, criados pela nossa imaginação.
c) A Geometria, segundo Euclides, não se aplica no mundo real é apenas imaginação do homem.
d) Segundo Euclides, na Geometria, o espaço é imaginário, depende do poder intuitivo de cada um.
A
Q02: Observe a figura a seguir, que representa uma cadeira:
B
Quatro alunos da primeira série formularam as seguintes afirmativas de acordo
com a figura apresentada:
Carlos - Os pontos A, C e E são colineares.
Patrícia - São coplanares os pontos E, B, D e J.
Alex - Os pontos C, D, E e F são coplanares.
Letícia - Os pontos A, C e I não são colineares.
Marque a opção que apresenta o nome do(a) aluno(a) que formulou uma afirmativa
CORRETA.
a) Carlos
b) Patrícia
c) Alex
C
E
F
I
Ensino Fundamental – 2ª fase
J
G
d) Letícia
Q03: Observe a seguinte linha poligonal com a representação de alguns de seus pontos.
Marque a afirmativa CORRETA.
D
H
a) BC e DE são segmentos de reta paralelos.
b) O ângulo entre os segmentos de retas BC e CD é um ângulo reto.
c) AB e EF são segmentos de retas colineares por pertencerem à mesma linha poligonal.
d) Os segmentos de retas DE e EF são consecutivos e não colineares.
Q04: Os pontos A , B , C , D e E determinam, na reta abaixo, vários segmentos não nulos. O número de
segmentos determinados por esses pontos é igual a:
A
a) 4
b) 6
B
c) 8
C
D
E
d) 10
Q05: Se dois segmentos AM e MB são congruentes, então podemos afirmar que:
a) Os pontos A, B e M são colineares
b) Os pontos A, B e M não são colineares
c) M é ponto médio de AB
d) M pode ser ponto médio de AB
Q06: Os segmentos AB 8cm e BC 12cm são colineares. Sendo M , N e P , respectivamente, pontos
médios de AC , AB e BC assinale a sentença verdadeira
a) NM 4cm
b) MP 6cm
c) NP 2cm ou NP 10cm
d) NP 4cm ou NP 6cm
Q07: Grandeza é tudo aquilo que envolve medidas. Medir significa comparar quantitativamente uma
grandeza com uma unidade através de uma escala pré-definida. Nas medições, as grandezas sempre
devem vir acompanhadas de unidades. A seguir foram apresentados alguns instrumentos de medida com
seus respectivos nomes.
Sextante
Teodolito
Dinamômetro
Goniômetro
Fonte das Imagens: Site www.wikipedia.org/
Apenas um dos instrumentos de medida apresentados acima não pode ser utilizado para “medir
ângulos”. Marque, entre as opções a seguir, aquela que apresenta o nome desse instrumento.
a) Teodolito
b) Sextante
c) Dinamômetro
d) Goniômetro
Q08: Assinale a opção verdadeira:
a) O complemento do complemento de um ângulo é (900 - )
b) O complemento do complemento de um ângulo é
c) O suplemento do complemento de um ângulo é (900 - )
d) O suplemento do suplemento de um ângulo é (1800 - )
Q09: Embora tenha sido acreditado por muitos anos ter sido inventado por um funcionário do Bilhar
Brunswick chamado Bob Lemieux, em 1972, o jogo Air Hockey foi realmente inventado por um trio de
engenheiros - Phil Crossman, Bob Kendrick, e Brad Baldwin - que estavam tentando criar uma jogo
Ensino Fundamental – 2ª fase
utilizando uma superfície sem atrito, por volta de 1969. O que é certo é que o original de patentes
referencia Phil Crossman, que, juntamente com os outros engenheiros, foi pioneiro na superfície da mesa
de fricção.Você já deve ter visto desse brinquedo principalmente nas áreas reservadas aos jogos nos
Shoppings.Dependendo da estratégia do jogador, ele pode fazer com que o disco rebata várias vezes nas
bordas da mesa. Analise a representação matemática de algumas jogadas.
Fonte:Site gamesdownload.com.br
Responda cada item a seguir:
a) Escreva qual conceito matemático podemos relacionar ao movimento do disco quando o mesmo
rebate na borda da plataforma e faz com que ele mude sua direção de propagação.
b) Escreva o nome de uma unidade de medida utilizada para medir ângulos.
c) Escreva as Classificações dos Ângulos quanto ao valor dos mesmos.
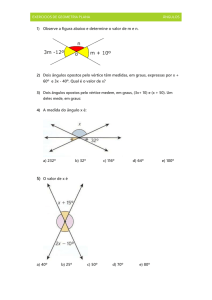
Q10: Observe os ângulos indicados na figura a seguir.
Marque a alternativa CORRETA relativa à classificação desses ângulos.
a) Os ângulos  e B̂ são consecutivos.
c) Os ângulos  e Ĉ são ângulos suplementares.
b) Â e Ĉ são ângulos adjacentes.
d) Â , B̂ e Ĉ são ângulos complementares.
Q11: As placas de sinalização podem ser encontradas ao lado ou suspensas sobre a pista, transmitindo
mensagens mediante legendas e/ou símbolos pré-conhecidos e legalmente instituídos. Sua finalidade é a
de manter o fluxo de trânsito em ordem e segurança. São três as espécies de placas: de regulamentação,
advertência e indicação. As placas de advertência indicam aos condutores os perigos que não lhes sejam
perceptíveis. Suas mensagens têm caráter de recomendação. São de forma
quadrada, nas cores amarela e preta e sua colocação é tal que suas diagonais ficam
nas posições vertical e horizontal. Observe o desenho de uma dessas placas ao lado.
Marque a afirmativa CORRETA a seguir que pode ser associada à placa de
advertência apresentada na figura.
a) Dois ângulos adjacentes e suplementares podem ser ambos agudos.
b) Dois ângulos adjacentes e suplementares podem ser ambos obtusos.
c) Dois ângulos adjacentes e suplementares podem ser um agudo e outro obtuso.
d) Dois ângulos adjacentes e suplementares podem ser ambos retos.
Entroncamento
Oblíquo à Direita
Q12: Dois ângulos são suplementares quando a soma de suas medidas é 180º. Nesse caso, cada ângulo
é o suplemento do outro. Analise as seguintes afirmativas a seguir:
Ensino Fundamental – 2ª fase
I - Dois ângulos adjacentes e suplementares formam um ângulo raso.
II - O suplemento de um ângulo reto é um ângulo reto.
III - Dois ângulos agudos podem ser suplementares.
IV - O suplemento de um ângulo raso é um ângulo nulo.
Marque a afirmativa CORRETA.
a) Apenas a afirmativa III é falsa.
c) Apenas a afirmativa IV é falsa.
b) Apenas as afirmativas I e II são verdadeiras.
d) Todas as afirmativas são verdadeiras.
Q13: Um avião, ao levantar voo, forma com o solo um ângulo ĝ no valor de 9º 20’ 44’. Calcule o valor do
ângulo ĥ , representado na figura a seguir, sabendo que os ângulos ĝ e ĥ são adjacentes e
suplementares.
ĥ
ĝ
Solo
Q14: Observe, atentamente, a figura a seguir:
Marque a afirmativa CORRETA relacionada aos ângulos determinados pelas retas concorrentes da figura
acima.
a) Os ângulos y e 32º 18’ 20” são ângulos opostos pelo vértice, portanto são suplementares.
b) A soma dos ângulos x e z é um ângulo agudo, porque os mesmos são opostos pelo vértice.
c) O valor do ângulo z na figura apresentada é de 147º 41’ 40”, suplemento do ângulo de 32º 18’ 20”.
d) É impossível calcular o valor do ângulo determinado pela bissetriz do ângulo x.
Q15: Observe atentamente a figura a seguir:
Sabendo que H Î J mede 41º 39” e J Î L mede 22º 20’ 45”, calcule o
ângulo formado pela bissetriz do ângulo H Î L .
Q16: Na figura a seguir OX é bissetriz do ângulo AÔB e OY é bissetriz
de BÔC .
Ensino Fundamental – 2ª fase
Marque a seguir a afirmativa CORRETA:
a) O ângulo 4x + 5º é o dobro do ângulo de 2x - 5º.
b) O valor de x poderá ser calculado através da equação: 4x + 5º - (2x - 5º) = 90º.
c) O valor do ângulo formado pelas bissetrizes dos ângulos AÔB e BÔC é 90º.
d) O ângulo formado pela bissetriz do ângulo AÔB possui valor de 15º.
Q17: Observe a figura
C
B
D
.
O
E
A
Se OA e OE são semi-retas opostas, EOˆ C 75 0 e OC é bissetriz do ângulo BOˆ D , o valor do ângulo
AOˆ C é:
a) 105o .
b) 125o .
c) 130o .
d) 135o .
Q18: As barras estabilizadoras constituem um elemento muito importante para o comportamento dinâmico
de um carro de rádio controle. Estes dispositivos proporcionam uma união elástica entre as suspensões
direita e esquerda de um mesmo eixo, o que significa que servem de união mecânica entre estes dois
semi-eixos de um mesmo eixo, o que pressupõe uma diferença eficaz quando um veículo descreve uma
curva.No automodelismo de rádio controle, as barras estabilizadoras são, geralmente, no formato de um
trapézio.
Analise uma representação matemática de uma dessas barras com
alguns de seus ângulos, 46º e 36º, mostrada a seguir. O ângulo
agudo é o ângulo formado pelas bissetrizes dos dois outros
ângulos.
Bissetri
z
46
º
Bissetri
z
36
º
Fonte: Site radiomodelismo.com.pt
Marque a alternativa que possui o valor correto do ângulo .
a) 72º .
b) 67º .
c) 41º .
d) 39º .
Q19: Nós possuímos, no nosso cérebro, circuitos de reconhecimento de padrões que nos fazem enxergar
um mundo cheio de geometria. Em outras palavras, o inconsciente cria significados para as formas e se
conhecermos a "linguagem da mente", podemos descobrir alguns significados ocultos. Então vamos a
alguns desses significados:
Triângulo para baixo: Passa a ideia de mobilidade
Triângulo para cima: Representa sucesso, dinamismo e estabilidade
Vejamos os exemplos: A Leroy Merlin e a Dicico, duas lojas de materiais de construção, usam o triângulo
para cima indicando sucesso com estabilidade, para passar a ideia de construção com solidez. A Top
Asiole Comunicações, que é uma agência de comunicação e marketing, usou o triângulo para mostrar sua
capacidade de conduzir os clientes ao sucesso com dinamismo.
Ensino Fundamental – 2ª fase
O retângulo em pé reforça a ideia de crescimento e sustentação. O HSBC, além de usar o quadrado como
base, trabalha com triângulos em várias direções, o que leva a juntar as definições: mobilidade, sucesso,
dinamismo e estabilidade.
Fonte: Centralblogs.com.br
Considerando um dos triângulos da “Asiole Comunicações” como o esquematizado a seguir, calcule o
valor dos ângulos representados pelas incógnitas x, y, z e t , sabendo que o segmento PA é bissetriz do
ângulo  do triângulo ABC.
Q20: Analise, atentamente, a figura representada a seguir:
Marque a opção que possui os pares de retas perpendiculares.
a)
b)
c)
d)
r
r
s
s
e
e
e
e
t
s
t
u
Ensino Fundamental – 2ª fase