Exercícios Resolvidos - Elementos de Matemática Finita

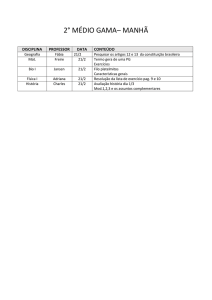
Elementos de Matemática Finita
Exercícios Resolvidos 2 - Congruências; Equações modulares
1. Seja m ∈ N, e a ∈ Z primo com m.
(a) Mostre que existem x, y ∈ Z tais que x ∈ [m]0 := {0, · · · , m − 1} e ax+ my =
1.
(b) Mostre que, na equação anterior, x é um inverso de a módulo m.
(c) Use o algoritmo de Euclides para encontrar um inverso (entre 1 e 114) de 22
módulo 115.
Resolução: (a) Uma vez que (a, m) = 1 sabemos (pela identidade de Bézout)
que existem inteiros x0 , y0 tais que ax0 + my0 = 1. Também sabemos que a
solução geral desta equação é x = x0 − km, y = y0 + ka, para certo k ∈ Z.
Assim, supondo km + x = x0 positivo, o que é sempre possível, e k a parte
inteira da divisão de de x0 por m, o valor x representa o resto da mesma
divisão, e como tal, x ∈ {0, · · · , m − 1} como pretendido.
(b) Usando a equação ax + my = 1 vemos que ax + my ≡ 1 (modm) o que
equivale a ax ≡ 1 (modm). Por definição, isto significa que x é inverso de
a módulo m.
(c) Para encontrar o inverso de a = 22 módulo m = 115, encontremos os
coeficientes x, y tais que 22x + 115y = 1. Como 115 = 22 · 5 + 5, 22 = 5 · 4 + 2
e 5 = 2 · 2 + 1 temos
1 = 5−2·2 = 5−2(22−5·4) = 9·5−2·22 = 9(115−5·22)−2·22 = (−47)·22+9·115
De acordo com a alínea (b), temos então que 68 ≡ −47 mod 115 é o inverso
de 22 pedido.
2. Resolva as seguintes equações ou mostre que não têm soluções:
(a) 210 x ≡ 10 mod 745
(b) 5(x2 + 1) ≡ 7 mod 24
Resolução: (a) Uma vez que mdc(210, 10, 745) = 5, podemos começar por encontrar uma solução dividindo a equação por 5. Assim, temos 42x ≡ 2 mod 149.
Trata-se de inverter 42 módulo 149. Usando o algoritmo de Euclides, temos
1
149 = 42 · 3 + 23, 42 = 23 + 19, 23 = 19 + 4, 19 = 4 · 4 + 3, 4 = 3 + 1. Assim,
1 = 4−3
= 4 − (19 − 4 · 4)
= −19 + 5 · (23 − 19)
= 5 · 23 − 6 · (42 − 23)
= −6 · 42 + 11 · (149 − 3 · 42)
= −(6 + 33) · 42 + 11 · 149,
logo 42−1 ≡ −39 mod 149 e x ≡ 2 · (42)−1 ≡ 2 · (−39) ≡ 71 mod 149.
Assim, como 745 = 5 · 149 as 5 soluções da equação original são
x ≡ 71 + 149k,
k = 0, · · · , 4
mod 745.
(b) Fazendo uma mudança de variável, pomos y = x2 + 1. Assim temos
5y ≡ 7 mod 24. Como 5 é invertível módulo 24, e 5 · 5 = 25 ≡ 1 mod 24,
temos que
y ≡ 7 · (5)−1 ≡ 7 · 5 ≡ 35 ≡ 11 mod 24
é a única solução. Agora queremos resolver a equação x2 + 1 ≡ 11 mod 24,
ou seja x2 ≡ 10 mod 24. Usando o teorema chinês dos restos, isto equivale
a resolver simultaneamente as equações x2 ≡ 2 mod 8 e x2 ≡ 1 mod 3.
A primeira equação não tem solução, pois em Z8 (ou seja, módulo 8) temos
1 · 1 = (−1) · (−1) ≡ 1, 2 · 2 = (−2) · (−2) ≡ 4, 3 · 3 = (−3) · (−3) ≡ 1,
4 · 4 ≡ 0. Assim, a equação inicial não tem soluções.
3. Resolva o seguinte sistema de congruências
(
x2 ≡ 2
mod 7
3
x ≡1
mod 9
Resolução: Primeiro verificamos quais as classes de congruência dos quadrados
módulo 7, e dos cubos módulo 9. Assim, módulo 7, temos 2 · 2 ≡ 4, 3 · 3 ≡
4 · 4 ≡ 2, pelo que as classes possíveis são 3 e −3 ≡ 4 módulo 7. Módulo
9 temos, 13 ≡ −(−1)3 ≡ 1 claro, e 23 ≡ −(−2)3 ≡ −1, 33 ≡ (−3)3 ≡ 0,
43 ≡ −(−4)3 ≡ 1. Assim, as possíveis classes para a segunda equação são
1, 4 ou −2 ≡ 7 mod 9. Temos então que resolver o sistema
(
x ≡ a1
mod 7
x ≡ a2
mod 9,
onde a1 ∈ {3, −3} e a2 ∈ {−2, 1, 4}. Uma vez que (7, 9) = 1, a solução geral
deste sistema é
M
M
b1 + a2
b2 ,
mod M
x ≡ a1
m1
m2
M −1
onde m1 = 7, m2 = 9, M = m1 m2 = 63 e, bi ≡ ( m
)
i
M
M
Uma vez que m1 = 9 e m2 = 7, temos
b1 ≡ 9−1
mod 7,
2
b2 ≡ 7−1
mod 9.
mod mi , i = 1, 2.
As soluções são então b1 ≡ 4 mod 7, e b2 ≡ 4
x ≡ 36 a1 + 28 a2
mod 9, e obtemos
mod 63.
Mais explicitamente, temos 6 soluções módulo 63, correspondendo aos 6 casos
(2 para a1 e 3 para a2 )
x ∈ {−11, −10, 4, 25, 31, 46}.
3