1 1. (Uema 2015) Um estudante analisou uma criança

1. (Uema 2015) Um estudante analisou uma criança brincando em um escorregador o qual
tem uma leve inclinação.
A velocidade foi constante em determinado trecho do escorregador em razão de o(a)
a) aceleração ter sido maior que zero.
b) atrito estático ter sido igual a zero.
c) atrito estático ter sido menor que o atrito cinético.
d) atrito estático ter sido igual ao atrito cinético.
e) aceleração ter sido igual a zero.
2. (Pucrj 2015) Um bloco metálico de massa 2,0 kg é lançado com velocidade de 4,0 m / s a
partir da borda de um trilho horizontal de comprimento 1,5 m e passa a deslizar sobre esse
trilho. O coeficiente de atrito cinético entre as superfícies vale 0,2. Cada vez que colide com as
bordas, o disco inverte seu movimento, mantendo instantaneamente o módulo de sua
velocidade.
Quantas vezes o disco cruza totalmente o trilho, antes de parar?
Considere: g  10 m / s2
a)
b)
c)
d)
e)
0
1
2
3
4
3. (Pucrj 2015) Uma caixa de massa m1  1,0 kg está apoiada sobre uma caixa de massa
m2  2,0 kg, que se encontra sobre uma superfície horizontal sem atrito. Existe atrito entre as
duas caixas. Uma força F horizontal constante é aplicada sobre a caixa de baixo, que entra em
movimento com aceleração de 2,0 m / s2 . Observa-se que a caixa de cima não se move em
relação à caixa de baixo.
O módulo da força F, em newtons, é:
a) 6,0
b) 2,0
c) 4,0
d) 3,0
e) 1,5
1
4. (Ufrgs 2015) Dois blocos, 1 e 2, são arranjados de duas maneiras distintas e empurrados
sobre uma superfície sem atrito, por uma mesma força horizontal F. As situações estão
representadas nas figuras I e II abaixo.
Considerando que a massa do bloco 1 é m1 e que a massa do bloco 2 é m2  3m1, a opção
que indica a intensidade da força que atua entre blocos, nas situações I e II, é,
respectivamente,
a) F / 4 e F / 4.
b) F / 4 e 3F / 4.
c) F / 2 e F / 2.
d) 3F / 4 e F / 4.
e) F e F.
5. (Epcar (Afa) 2015) Uma determinada caixa é transportada em um caminhão que percorre,
com velocidade escalar constante, uma estrada plana e horizontal. Em um determinado
instante, o caminhão entra em uma curva circular de raio igual a 51,2 m, mantendo a mesma
velocidade escalar. Sabendo-se que os coeficientes de atrito cinético e estático entre a caixa e
o assoalho horizontal são, respectivamente, 0,4 e 0,5 e considerando que as dimensões do
caminhão, em relação ao raio da curva, são desprezíveis e que a caixa esteja apoiada apenas
no assoalho da carroceria, pode-se afirmar que a máxima velocidade, em m / s, que o
caminhão poderá desenvolver, sem que a caixa escorregue é
a) 14,3
b) 16,0
c) 18,0
d) 21,5
6. (Uece 2015) Um elevador, durante os dois primeiros segundos de sua subida, sofre uma
aceleração vertical para cima e de módulo 1m s2 . Sabe-se que também age sobre o elevador
a força da gravidade, cuja aceleração associada é 10m s2 . Durante esses dois primeiros
segundos do movimento, a aceleração resultante no elevador é, em m s2 ,
a) 1.
b) 10.
c) 9.
d) 11.
TEXTO PARA A PRÓXIMA QUESTÃO:
Considere os dados abaixo para resolver a(s) questão(ões) quando for necessário.
Constantes físicas
Aceleração da gravidade: g  10m / s2
Densidade da água: r  1,0 g / cm3
2
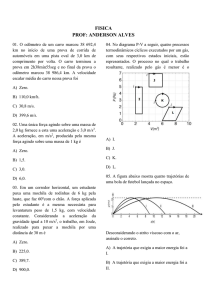
7. (G1 - cftmg 2015) A figura seguinte ilustra uma pessoa aplicando uma força F para direita
em uma geladeira com rodas sobre uma superfície plana.
Nesse contexto, afirma-se que:
I. O uso de rodas anula a força de atrito com o solo.
II. A única força que atua na geladeira é a força aplicada pela pessoa.
III. Ao usar rodas, a força de reação normal do piso sobre a geladeira fica menor.
IV. A geladeira exerce sobre a pessoa uma força oposta e de igual intensidade a F.
V. Se a geladeira se movimenta com velocidade constante, ela está em equilíbrio.
São corretas apenas as afirmativas
a) III e IV.
b) IV e V.
c) I, II e III.
d) I, II e V.
8. (Ifsc 2014) Ao saltar de paraquedas, os paraquedistas são acelerados durante um intervalo
de tempo, podendo chegar a velocidades da ordem de 200 km/h, dependendo do peso e da
área do seu corpo.
Quando o paraquedas abre, o conjunto (paraquedas e paraquedista) sofre uma força contrária
ao movimento, capaz de desacelerar até uma velocidade muito baixa permitindo uma
aterrissagem tranquila.
Assinale a soma da(s) proposição(ões) CORRETA(S).
01) A aceleração resultante sobre o paraquedista é igual à aceleração da gravidade.
02) Durante a queda, a única força que atua sobre o paraquedista é a força peso.
04) O movimento descrito pelo paraquedista é um movimento com velocidade constante em
todo o seu trajeto.
08) Próximo ao solo, com o paraquedas aberto, já com velocidade considerada constante, a
força resultante sobre o conjunto (paraquedas e paraquedista) é nula.
16) Próximo ao solo, com o paraquedas aberto, já com velocidade considerada constante, a
força resultante sobre o conjunto (paraquedas e paraquedista) não pode ser nula; caso
contrário, o conjunto (paraquedas e paraquedista) não poderia aterrissar.
3
32) A força de resistência do ar é uma força variável, pois depende da velocidade do conjunto
(paraquedas e paraquedista).
9. (G1 - ifce 2014) Na figura abaixo, o fio inextensível que une os corpos A e B e a polia têm
massas desprezíveis. As massas dos corpos são mA = 4,0 kg e mB = 6,0 kg. Desprezando-se
2
o atrito entre o corpo A e a superfície, a aceleração do conjunto, em m/s , é de (Considere a
2
aceleração da gravidade 10,0 m/s )
a) 4,0.
b) 6,0.
c) 8,0.
d) 10,0.
e) 12,0.
10. (Enem 2013) Uma pessoa necessita da força de atrito em seus pés para se deslocar sobre
uma superfície. Logo, uma pessoa que sobe uma rampa em linha reta será auxiliada pela força
de atrito exercida pelo chão em seus pés.
Em relação ao movimento dessa pessoa, quais são a direção e o sentido da força de atrito
mencionada no texto?
a) Perpendicular ao plano e no mesmo sentido do movimento.
b) Paralelo ao plano e no sentido contrário ao movimento.
c) Paralelo ao plano e no mesmo sentido do movimento.
d) Horizontal e no mesmo sentido do movimento.
e) Vertical e sentido para cima.
11. (Uff 2012) Ímãs são frequentemente utilizados para prender pequenos objetos em
superfícies metálicas planas e verticais, como quadros de avisos e portas de geladeiras.
Considere que um ímã, colado a um grampo, esteja em contato com a porta de uma geladeira.
Suponha que a força magnética que o ímã faz sobre a superfície da geladeira é perpendicular
a ela e tem módulo FM . O conjunto imã/grampo tem massa m0 . O coeficiente de atrito estático
entre a superfície da geladeira e a do ímã é e . Uma massa M está pendurada no grampo por
um fio de massa desprezível, como mostra a figura.
4
a) Desenhe no diagrama as forças que agem sobre o conjunto ímã/grampo (representado
pelo ponto preto no cruzamento dos eixos x e y na figura), identificando cada uma dessas
forças.
b) Qual o maior valor da massa M que pode ser pendurada no grampo sem que o conjunto
caia?
12. (Enem PPL 2012) O freio ABS é um sistema que evita que as rodas de um automóvel
sejam bloqueadas durante uma frenagem forte e entrem em derrapagem. Testes demonstram
que, a partir de uma dada velocidade, a distância de frenagem será menor se for evitado o
bloqueio das rodas.
O ganho na eficiência da frenagem na ausência de bloqueio das rodas resulta do fato de
a) o coeficiente de atrito estático tornar-se igual ao dinâmico momentos antes da derrapagem.
b) o coeficiente de atrito estático ser maior que o dinâmico, independentemente da superfície
de contato entre os pneus e o pavimento.
c) o coeficiente de atrito estático ser menor que o dinâmico, independentemente da superfície
de contato entre os pneus e o pavimento.
d) a superfície de contato entre os pneus e o pavimento ser maior com as rodas
desbloqueadas, independentemente do coeficiente de atrito.
e) a superfície de contato entre os pneus e o pavimento ser maior com as rodas
desbloqueadas e o coeficiente de atrito estático ser maior que o dinâmico.
13. (G1 - ifpe 2012) O sistema da figura é formado por um bloco de 80 kg e duas molas de
massas desprezíveis associadas em paralelo, de mesma constante elástica. A força horizontal

F mantém o corpo em equilíbrio estático, a deformação elástica do sistema de molas é 20 cm
2
e a aceleração da gravidade local tem módulo 10 m/s . Então, é correto afirmar que a
constante elástica de cada mola vale, em N/cm:
a) 10
b) 20
c) 40
d) 60
e) 80
5
14. (Unesp 2011) Observe a tirinha
Uma garota de 50 kg está em um elevador sobre uma balança calibrada em newtons. O
elevador move-se verticalmente, com aceleração para cima na subida e com aceleração para
baixo na descida. O módulo da aceleração é constante e igual a 2m / s2 em ambas situações.
Considerando g  10m / s2 , a diferença, em newtons, entre o peso aparente da garota,
indicado na balança, quando o elevador sobe e quando o elevador desce, é igual a
a) 50.
b) 100.
c) 150.
d) 200.
e) 250.
15. (Upf 2015) A queda de um elevador em um prédio no centro de Porto Alegre no final de
2014 reforçou as ações de fiscalização nesses equipamentos, especialmente em relação à
superlotação. A partir desse fato, um professor de Física resolve explorar o tema em sala de
aula e apresenta aos alunos a seguinte situação: um homem de massa 70 kg está apoiado
numa balança calibrada em newtons no interior de um elevador que desce à razão de 2 m / s2 .
Considerando g  10 m / s2, pode-se afirmar que a intensidade da força indicada pela balança
será, em newtons, de:
a) 560
b) 840
c) 700
d) 140
e) 480
16. (Uece 2014) Uma criança desliza em um tobogã muito longo, com uma aceleração
constante. Em um segundo momento, um adulto, com o triplo do peso da criança, desliza por
esse mesmo tobogã, com aceleração também constante. Trate os corpos do adulto e da
criança como massas puntiformes e despreze todos os atritos. A razão entre a aceleração do
adulto e a da criança durante o deslizamento é
a) 1.
b) 2.
c) 1/3.
d) 4.
17. (Enem 2013) Em um dia sem vento, ao saltar de um avião, um paraquedista cai
verticalmente até atingir a velocidade limite. No instante em que o paraquedas é aberto
(instante TA), ocorre a diminuição de sua velocidade de queda. Algum tempo após a abertura
do paraquedas, ele passa a ter velocidade de queda constante, que possibilita sua
aterrissagem em segurança.
Que gráfico representa a força resultante sobre o paraquedista, durante o seu movimento de
queda?
6
a)
b)
c)
d)
e)
18. (Upe 2013) Suponha um bloco de massa m = 2 kg inicialmente em repouso sobre um
plano horizontal sem atrito. Uma força F = 16 N é aplicada sobre o bloco, conforme mostra a
figura a seguir.
Qual é a intensidade da reação normal do plano de apoio e a aceleração do bloco,
2
respectivamente, sabendo-se que sen 60° = 0,85, cos 60° = 0,50 e g = 10 m/s ?
2
a) 6,4 N e 4 m/s
2
b) 13, 6 N e 4 m/s
2
c) 20,0 N e 8 m/s
7
2
d) 16,0 N e 8 m/s
2
e) 8,00 N e 8 m/s
TEXTO PARA A PRÓXIMA QUESTÃO:
Dois blocos, de massas m 1=3,0 kg e m2=1,0 kg, ligados por um fio inextensível, podem deslizar
sem atrito sobre um plano horizontal. Esses blocos são puxados por uma força horizontal F de
módulo F=6 N, conforme a figura a seguir.
(Desconsidere a massa do fio).
19. (Ufrgs 2012) As forças resultantes sobre m 1 e m2 são, respectivamente,
a) 3,0 N e 1,5 N.
b) 4,5 N e 1,5 N.
c) 4,5 N e 3,0 N.
d) 6,0 N e 3,0 N.
e) 6,0 N e 4,5 N.
20. (Uerj 2013) Um bloco de madeira encontra-se em equilíbrio sobre um plano inclinado de
45º em relação ao solo. A intensidade da força que o bloco exerce perpendicularmente ao
plano inclinado é igual a 2,0 N. Entre o bloco e o plano inclinado, a intensidade da força de
atrito, em newtons, é igual a:
a) 0,7
b) 1,0
c) 1,4
d) 2,0
8
Gabarito:
Resposta da questão 1:
[E]
Se a velocidade é constante, significa que a força resultante é nula, sendo assim, de acordo
com o princípio fundamental da dinâmica, a aceleração também será nula.
Resposta da questão 2:
[C]
Considerando que o movimento acontece na horizontal, a única força que age na direção do
deslocamento é a força de atrito, sendo contrária ao sentido de movimento provocará uma
desaceleração responsável por parar o bloco por completo. Sendo assim a força resultante é a
força de atrito.
Fr  Fat
Usando o Princípio Fundamental da Dinâmica e a expressão para a Força de atrito:
m  a  μ  m  g
A aceleração será:
a  μ  g  0,2  10 m / s2
a  2 m / s2
Do MRUV usamos a equação de Torricelli:
v2  v02  2  a  Δs
A distância total percorrida será:
Δs 
v 2  v 02
2a
Δs 
0  42
16

4m
2   2 
4
Logo, o número de vezes que o disco cruza totalmente o trilho é:
4m
n
 2,667 vezes
1,5 m
A distância corresponde a dois trilhos inteiros e mais uma fração de 2/3 do trilho
Então,
n2
Resposta da questão 3:
[A]
Como a caixa superior se move junto com a caixa inferior, não há aceleração diferente entre
elas e podemos considerar como sendo um corpo único.
E pela 2ª lei de Newton:
F  ma
F  (2 kg  1 kg)  2 m / s2
F6N
9
Resposta da questão 4:
[D]
Nos dois casos a aceleração tem mesmo módulo:
F  m1  m2  a  F  m1  3 m1  a  F  4 m1 a  a 
F
.
4 m1
Calculando as forças de contato:

3F
F
 F12 
.
F12  m2 a  F12  3 m1
4 m1
4


F
F

F21  m1 a  F21  m1 4 m  F21  4 .
1

Resposta da questão 5:
[B]
No movimento circular uniforme, a resultante das forças radiais é a força centrípeta:
Fr  Fc 
m  v2
R
A única força radial é a força de atrito que, dependendo da velocidade, impede que a caixa seja
deslocada dentro do caminhão, sendo a resultante centrípeta.
horizontal
Fr  Fat  μ  N 
Fat  μ  m  g
Igualando as duas equações:
m  v2
 μ mg
R
Isolando v:
v  μ R  g
Substituindo os valores, temos a velocidade máxima para a caixa não escorregar na carroceria:
v  0,5  51,2  10  256  16 m / s
Resposta da questão 6:
[A]
Como o elevador está subindo acelerado, a tração no cabo tem módulo maior que a força
gravitacional, de forma a anular esta força e ainda imprimir uma aceleração vertical para cima.
10
Desta forma, se o elevador está subindo, com aceleração vertical para cima e de módulo
1m s2 , logo esta é exatamente a aceleração resultante do elevador.
Resposta da questão 7:
[B]
[I] Incorreta. O uso de rodas não anula a força de atrito com o solo. Entre o solo e as rodas
não há atrito de escorregamento mas há atrito de rolamento.
[II] Incorreta. Além da força aplicada pela pessoa há também o peso e a força de contato com
o solo, cujas componentes são a normal e o atrito.
[III] Incorreta. Se a força aplicada pela pessoa é horizontal, a força de reação normal do piso
sobre a geladeira tem a mesma intensidade do peso, com ou sem rodas, pois a geladeira
está em equilíbrio na direção vertical.
[IV] Correta. De acordo com o Princípio da Ação-Reação, a geladeira exerce sobre a pessoa
uma força oposta e de igual intensidade a F.
[V] Correta. Se a geladeira se movimenta com velocidade constante, ela está em equilíbrio
dinâmico, pois está em movimento retilíneo e uniforme.
Resposta da questão 8:
08 + 32 = 40.
Justificando as proposições incorretas:
[01] Incorreta. A resistência do ar não é desprezível, impedindo a queda livre.
[02] Incorreta. Atuam no paraquedista o peso e a resistência do ar.
[04] Incorreta. O movimento é acelerado no início da queda.
[08] Correta.
[16] Incorreta. De acordo com o Princípio da Inércia, se o movimento é retilíneo e uniforme a
resultante das forças sobre o corpo é nula.
[32] Correta.
Resposta da questão 9:
[B]
Aplicando o Princípio Fundamental da Dinâmica ao sistema:
PB  mA  mB  a  60  10 a  a  6 m/s2.
Resposta da questão 10:
[C]
Quando a pessoa anda, ela aplica no solo uma força de atrito horizontal para trás. Pelo
Princípio da Ação-Reação, o solo aplica nos pés da pessoa uma reação, para frente (no
sentido do movimento), paralela ao solo.
Resposta da questão 11:
a)
11
P : peso do corpo suspenso;
P0 : peso do conjunto ímã/grampo;
Fmag : força magnética;
Fat : componente de atrito da força que
a superfície da geladeira exerce no
conjunto;
N : componente normal da força que
a superfície da geladeira exerce no
conjunto;
b) O maior valor da massa M do corpo que pode ser pendurado sem que o conjunto
ímã/grampo caia é aquele valor que coloca o conjunto na iminência de escorregar, ou seja,
quando a componente de atrito atinge intensidade máxima Fat
.
máx

Assim, do equilíbrio:
Eixo x: N  Fmag

Eixo y: F
at máx  P  P0

μ e Fmag  m0 g
M

g
M
μ e Fmag
g

 μ e N  M g  m0 g  μe Fmag  M g  m0 g 
 m0 .
Resposta da questão 12:
[B]
O freio ABS é mais eficiente, pois impede o travamento das rodas, fazendo a frenagem com
força de atrito estática, que é maior que a dinâmica, pois o coeficiente de atrito estático e maior
que o dinâmico.
Resposta da questão 13:
[B]
Notamos que 2 molas seguram o bloco. Desta forma,
12
2F  elástica   Peso
2k  x  mg
2k   20   80  10
40 k  800
k  800/40  20 N/cm
Resposta da questão 14:
[D]
Elevador subindo: N1  P  ma  N1  500  50x2  N1  600N
Elevador descendo: P  N2  ma  500  N2  50x2  N2  400N
N1  N2  600  400  200N .
Resposta da questão 15:
[A]
A figura abaixo ilustra a situação física:
Como o diagrama de corpo livre nos mostra, a força resultante a pessoa é:
FR  P  N
Usando o Princípio Fundamental da Dinâmica (2ª lei de Newton):
FR  m  a
Igualando as duas equações e isolando a força normal, temos:
P N  ma
N  m g  a


N  70 kg 10 m / s2  2 m / s2  560 N
Resposta da questão 16:
[A]
A figura mostra as forças que agem sobre o bloco e as componentes do peso.
13
Na direção paralela ao plano inclinado, a resultante é a componente tangencial do peso.
Aplicando o Princípio Fundamental da Dinâmica:
Px  m a  m g sen θ  m a  a  g sen θ.
Como se pode notar, a intensidade da aceleração independe da massa, tendo o mesmo valor
para a criança e para o adulto. Assim:
aadulto
 1.
acriança
Resposta da questão 17:
[B]
No início da queda, a única força atuante sobre o paraquedista (homem + paraquedas) é
apenas o peso [para baixo (+)]. À medida que acelera, aumenta a força de resistência do ar,
até que a resultante se anula, quando é atingida a velocidade limite. No instante (TA) em que o
paraquedas é aberto, a força de resistência do ar aumenta abruptamente, ficando mais intensa
que o peso, invertendo o sentido da resultante [para cima (-)]. O movimento passa a ser
retardado até ser atingida a nova velocidade limite, quando a resultante volta a ser nula.
Resposta da questão 18:
[A]
A figura abaixo mostra as forças que agem no bloco.
As forças verticais anulam-se. Ou seja:
N  Fsen60  P  N  16x0,85  20  N  20  13,6  6,4N
Na horizontal FR  ma  Fcos60  ma  16x0,5  2a  a  4,0 m/s2
Resposta da questão 19:
[B]
14
Aplicando o Princípio Fundamental da Dinâmica para calcular o módulo da aceleração do
sistema e, a seguir, o mesmo princípio em cada corpo:
6
F   m1  m2  a  6   3  1 a  a 
 a  1,5 m / s2 .
4
R1  m1 a  3 1,5   R1  4,5 N.

R2  m2 a  11,5   R2  1,5 N.
Resposta da questão 20:
[D]
Dado: N  2 N; θ  45.
A figura ilustra a situação.
O bloco está sujeito a duas forças: O peso P  e a força aplicada pelo plano F  . Como ele
está em equilíbrio, a resultante dessas forças é nula, ou seja, elas têm mesma intensidade e
sentidos opostos.
Assim, da figura:
F
F
tg 45  at  1  at  Fat  2 N.
N
2
15