Estudo dos Polígonos - curso de matemática imes

Instituto Municipal de Ensino Superior de Catanduva – SP
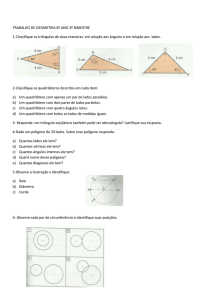
Curso de Licenciatura em Matemática – 2º ano – Prática de Ensino da Matemática II
Prof. M.Sc. Fabricio Eduardo Ferreira –– [email protected]
Estudo dos Polígonos
A palavra polígono é a união de dois radicais poli (muitos) e gonos (ângulos). Desta forma a palavra polígono significa,
originalmente, “figura com muitos ângulos”.
Por definição um polígono é uma figura plana, simples, fechada formada apenas por segmentos de retas. Simples pois
nenhum de seus lados pode interceptar o outro, fechada pois não conseguimos identificar suas extremidades.
Figura 1a: Não é um polígono
pois é uma figura aberta
Figura 1b: Não é um polígono
pois não é uma figura simples
Figura 1c: Não é um polígono pois nem
todos lados são segmentos de retas
Todo polígono possui lados que são os lados segmentos de retas que o compõe, vértices que são os pontos de interseção
entre os lados do polígono, e ângulos definidos pelas regiões delimitadas pelos lados. Desta forma os polígonos possuem
ângulos internos e ângulos externos.
Na figura 2 temos o polígono 𝐴𝐵𝐶𝐷𝐸 que apresenta:

̅̅̅̅ , ̅̅̅̅
os lados ̅̅̅̅
𝐴𝐵 , 𝐵𝐶
𝐶𝐷, ̅̅̅̅
𝐷𝐸 e ̅̅̅̅
𝐸𝐴;

os vértices 𝐴, 𝐵, 𝐶, 𝐷 e 𝐸;

̂ 𝐸 e 𝐷𝐸̂ 𝐴;
os ângulos internos 𝐸𝐴̂𝐵, 𝐴𝐵̂ 𝐶, 𝐵𝐶̂ 𝐷, 𝐶𝐷

̂ 𝐶 e 𝐷𝐸̂ 𝐺.
os ângulos externos 𝐹𝐴̂𝐸, 𝐽𝐵̂ 𝐴, 𝐼𝐶̂ 𝐵, 𝐻𝐷
Figura 2: Polígono 𝑨𝑩𝑪𝑫𝑬
Geralmente há uma confusão entre polígono e região poligonal. De acordo com sua definição o polígono é formado apenas
pelos segmentos de retas, sendo que a região do plano delimitada por tais segmentos (região poligonal) não faz parte do
polígono. Atividades que envolvem a construção de polígonos com palitos de sorvete, canudinhos plásticos, barbantes ou
outros materiais são importantes para que o aluno crie esta distinção.
Figura 3a: Polígono 𝑨𝑩𝑪𝑫𝑬𝑭
Figura 3b: Região poligonal 𝑨𝑩𝑪𝑫𝑬𝑭
Em todo polígono o número de ângulos, de lados e de vértices é sempre igual. Daí o porquê de, em algumas obras didáticas,
o significado de polígonos é “figura com muitos lados”.
Obedecendo a definição não há polígono com apenas um lado, ou dois lados. O menor número de lados que um polígono
pode ter são 3 lados. De acordo com o número de lados o polígono recebe nomenclatura especial:
Tabela 1: Nomenclatura dos Polígonos de acordo com seu número de lados
Número de lados
3
4
5
6
7
8
9
Nome do Polígono
triângulo
quadrilátero
pentágono
hexágono
heptágono
octógono
eneágono
Número de lados
10
11
12
15
20
100
1000
Nome do Polígono
decágono
undecágono
dodecágono
pentadecágono
icoságono
hectógono
quilógono
Diagonais de um polígono
Uma diagonal de um polígono é um segmento de reta que une um vértice a outro vértice não adjacente, ou seja, um outro
vértice que não seja consecutivo ao primeiro.
Figura 4: Diagonal 𝑨𝑪 do polígono 𝑨𝑩𝑪𝑫
Caso todas as diagonais de um polígono situem-se em sua região interna o polígono é considerado polígono convexo; no
caso contrário o polígono é considerado não convexo.
Figura 5a: Polígono convexo pois
todas suas diagonais estão em sua região interna
Figura 5b: Polígono não convexo pois há pelo menos uma
diagonal que não encontra-se em sua região interna
Desta forma temos algumas conclusões sobre o número de diagonais de um polígono:
 o triângulo é o único polígono que não possui diagonais (todos seus vértices estão ligados entre si);
 o quadrilátero é o único polígono que possui o número de lados como sendo o dobro do número de diagonais;

o pentágono é o único polígono que possui o número de lados coincidindo com seu número de diagonais;
Estudo dos triângulos
Os triângulos estão entre os polígonos mais estudados na Geometria. Isto se deve pois as estruturas triangulares são aquelas
que propiciam maior rigidez nas construções, sendo necessárias desde a Antiguidade.
Um triângulo é um polígono que possui três lados, três vértices, três ângulos internos e três ângulos externos.
Basicamente há duas maneiras distintas de classificarmos um triângulo: de acordo com a medida de seus lados e de acordo
com o tipo de seus ângulos internos.
Tabela 2: Classificação dos triângulos
Classificação de acordo com a medida de seus lados
Classificação de acordo com a medida de seus ângulos
a) Triângulo equilátero: é aquele que possui todos seus i) Triângulo acutângulo: é aquele que possui todos seus
lados congruentes;
ângulos agudos;
b) Triângulo isósceles: é aquele que possui dois lados ii) Triângulo retângulo: é aquele que possui um ângulo
congruentes;
reto;
c) Triângulo escaleno: é aquele que não possui lados iii) Triângulo obtusângulo: é aquele que possui um ângulo
congruentes entre si.
obtuso.
Muitos alunos acreditam que tais classificações se excluem mutuamente, ou seja, se um triângulo é equilátero ele não pode
ser acutângulo, o que não é verdade. Exercícios que explorem a possibilidade do aluno classificar triângulos de acordo com
ambas classificações são importantes para mostrar que isto é possível.
Um teorema importante no estudo dos triângulos afirma que “o número de ângulos congruentes de um triângulo corresponde
ao número de lados congruentes do mesmo triângulo”, ou seja, um triângulo que possui dois ângulos congruentes também
terá, por consequência, dois ângulos iguais. Desta forma podemos concluir que todo triângulo equilátero também será
equiângulo (possui todos seus ângulos congruentes), sendo sua recíproca verdadeira também.
Soma dos ângulos internos de um triângulo qualquer
Solicite inicialmente que os alunos recortem um triângulo qualquer numa folha de papel. Em seguida peça aos alunos que
destaquem os ângulos internos do triângulo. Recortando os três ângulos internos, peça para os alunos que encaixem um
ângulo ao lado do outro e expliquem o que conseguiram obter.
Figura 6a
Figura 6b
Figura 6c
Passos para experimentação da soma dos ângulos internos de um triângulo qualquer
O objetivo da atividade anterior é o aluno perceber que a soma dos ângulos internos de um triângulo qualquer é sempre
180º. A experiência não serve como demonstração, contudo é uma ótima atividade para aqueles alunos que se encontram
ainda no período de operações concretas.
De acordo com o nível da sala pode-se utilizar uma demonstração mais formal como a seguir:
Demonstração
Seja o triângulo 𝐴𝐵𝐶 cujas medidas de seus ângulo internos são 𝑎,
̂ 𝑏̂ e 𝑐̂, conforme pode ser observada na figura 7a. Pelo
̅̅̅̅ , conforme pode-se observar na figura 7b. Prolongando os lados 𝐴𝐵
̅̅̅̅ e 𝐴𝐶
̅̅̅̅ ,
vértice 𝐴 traçamos uma paralela ao lado 𝐵𝐶
̂ 𝑒̂ e 𝑓̂, conforme pode-se observar na figura 7c.
determinamos os ângulos 𝑑,
Figura 7a
i)
Figura 7b
Figura 7c
Desta forma temos que:
os ângulos 𝑎̂ e 𝑑̂ são congruentes pois são Opostos pelo Vértice;
ii) os ângulos 𝑏̂ e 𝑒̂ são congruentes pois são correspondentes;
iii) os ângulos 𝑐̂e 𝑓̂ são congruentes pois são correspondentes.
A soma dos ângulos internos do triângulo 𝐴𝐵𝐶 corresponde a soma 𝑆𝑖 :
𝑖) 𝑖𝑖) 𝑖𝑖𝑖)
𝑆𝑖 = 𝑎̂ + 𝑏̂ + 𝑐̂ ⇒
𝑆𝑖 = 𝑑̂ + 𝑒̂ + 𝑓̂ = 180°
Estudo dos quadriláteros
Os quadriláteros são polígonos que possuem quatro lados, quatro vértices, quatro ângulos internos e quatro ângulos
externos. Por serem muito presentes no cotidiano, o estudo dos quadriláteros e suas propriedades tem grande significância
na Geometria.
De acordo com suas características alguns quadriláteros são conhecidos por quadriláteros notáveis, sendo ele: o trapézio, o
paralelogramo, o retângulo, o losango e o quadrado. Seguem as definição de cada quadrilátero notável:
a) trapézio: é o quadrilátero que possui um par de lados paralelos;
b) paralelogramo: é o quadrilátero que possui dois pares de lados paralelos;
c) retângulo: é o quadrilátero que possui todos seus ângulos congruentes;
d) losango: é o quadrilátero que possui todos seus lados congruentes;
e) quadrado: é o quadrilátero que possui todos seus lados congruentes e todos seus ângulos congruentes.
Figura 8a:
Trapézio
Figura 8b:
Paralelogramo
Figura 8c:
Retângulo
Figura 8d:
Losango
Figura 8e:
Quadrado
Explorar a relação de inclusão entre os conjuntos de quadriláteros é uma boa atividade para fixar adequadamente as
definições dos mesmos. Por exemplo, todo retângulo é um paralelogramo, pois ele satisfaz as condições necessárias para
tal; enquanto que nem todo paralelogramo é retângulo, pois nem sempre apresenta ângulos com a mesma medida.