Problemas Resolvidos de Física

Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
HALLIDAY, RESNICK, WALKER, FUNDAMENTOS DE FÍSICA, 8.ED., LTC, RIO DE
JANEIRO, 2008.
FÍSICA 1
CAPÍTULO 4 – MOVIMENTO EM DUAS E TRÊS DIMENSÕES
13. A posição r de uma partícula que se move em um plano xy é dada por r = (2,00t3 − 5,00t)i +
(6,00 − 7,00t4)j com r em metros e t em segundos. Na notação de vetores unitários, calcule (a)
r, (b) v e (c) a para t = 2,00 s. (d) Qual é o ângulo entre o sentido positivo do eixo x e uma reta
tangente à trajetória da partícula em t = 2,00 s?
(Pág. 85)
Solução.
(a) Para t = 2,00 s, r vale r(2,00 s):
3
4
r( 2,00 s ) = ⎡ 2, 00 ( 2, 00 ) − 5, 00 ( 2, 00 ) ⎤ i + ⎡ 6, 00 − 7, 00 ( 2, 00 ) ⎤ j
⎣
⎦ ⎣
⎦
r( 2,00 s ) = ( 6, 00 m ) i + (106 m ) j
(b) A velocidade é a derivada da posição em relação ao tempo.
dr
v=
= ( 6, 00t 2 − 5, 00 ) i − 28, 0t 3 j
dt
Para t = 2,00 s, v vale v(2,00 s):
v ( 2,00 s ) = ⎡ 6, 00 ( 2, 00 ) − 5, 00 ⎤ i − 28, 0 ( 2, 00 ) j
⎣
⎦
2
3
v ( 2,00 s ) = (19, 0 m/s ) i + ( −224 m/s ) j
(c) A aceleração é a derivada da velocidade em relação ao tempo.
dv
a=
= 12, 0ti − 84, 0t 2 j
dt
a ( 2,00 s ) = 12, 0 ( 2, 00 ) i − 84, 0 ( 2, 00 ) j
2
(
) (
)
a ( 2,00 s ) = 24, 0 m/s 2 i − 336 m/s 2 j
(d) O cálculo do ângulo é feito a partir dos componentes x e y da velocidade em t = 2,00 s:
vy
( −224 m/s ) = 11, 7894 "
tan θ =
=
v x ( −19, 0 m/s )
Logo:
θ = tan −1 (11, 7894 ") = −85,1516 "D
θ ≈ −85, 2D
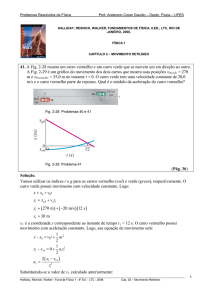
O gráfico paramétrico das funções x(t) e y(t), entre t = 0,00 s e t = 2,00 s é mostrado abaixo. O vetor
v(2,00 s) é mostrado na posição r(2,00 s). O ângulo θ aparenta ser menor do que 85,2o devido à
diferença nas escalas dos eixos.
________________________________________________________________________________________________________
a
Halliday, Resnick, Walker - Fund.de Física 1 - 8 Ed. - LTC - 2009.
Cap. 04 – Movimento em Duas e Três Dimensões
1
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
x m
-2
2
4
6
- 20
- 40
r(2,00 s)
- 60
- 80
- 100
θ
v(2,00 s)
________________________________________________________________________________________________________
a
Halliday, Resnick, Walker - Fund.de Física 1 - 8 Ed. - LTC - 2009.
Cap. 04 – Movimento em Duas e Três Dimensões
2