A saturação nos transformadores de distribuição e a corrente de

Modelamento de Saturação em Transformadores
O Circuito Equivalente do Transformador na Figura 1 pode ser modificado para incluir
os efeitos não-lineares da característica do núcleo. Esta modificação pode ser
conseguida pela substituição do indutor magnetizante na figura com uma impedância
não-linear. A característica fluxo-corrente desta impedância é escolhida de acordo com
a característica magnética do núcleo do transformador.
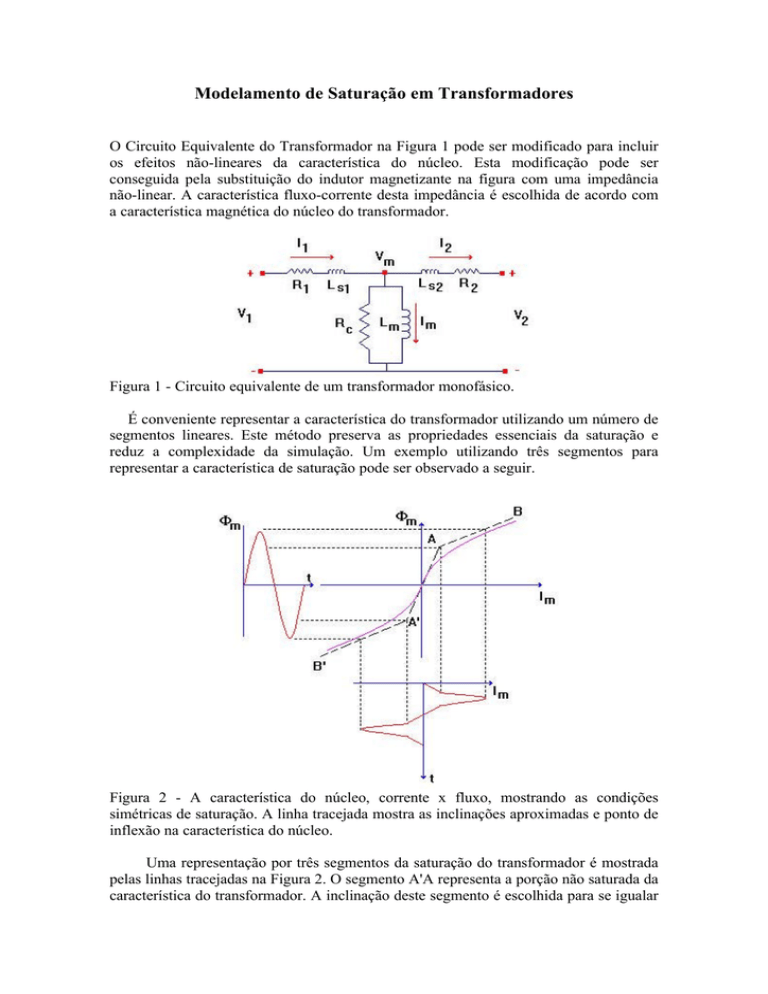
Figura 1 - Circuito equivalente de um transformador monofásico.
É conveniente representar a característica do transformador utilizando um número de
segmentos lineares. Este método preserva as propriedades essenciais da saturação e
reduz a complexidade da simulação. Um exemplo utilizando três segmentos para
representar a característica de saturação pode ser observado a seguir.
Figura 2 - A característica do núcleo, corrente x fluxo, mostrando as condições
simétricas de saturação. A linha tracejada mostra as inclinações aproximadas e ponto de
inflexão na característica do núcleo.
Uma representação por três segmentos da saturação do transformador é mostrada
pelas linhas tracejadas na Figura 2. O segmento A'A representa a porção não saturada da
característica do transformador. A inclinação deste segmento é escolhida para se igualar
à indutância de magnetização do transformador não saturada. Os segmentos B'A' e BA
representam respectivamente a porção saturada das regiões positiva e negativa da
característica do transformador. A inclinação destes segmentos é escolhida para se
igualar à indutância do núcleo de ar do transformador. O ponto no plano fluxo-corrente
onde o segmento com saturação intercepta o segmento linear da característica é definido
como o ponto do joelho de saturação. O ponto do joelho define o mínimo fluxo e
corrente de magnetização para a qual a saturação é apreciável.
A representação da característica é calculada como se segue. A partir dos ensaios
de rotina de um transformador de 300 kVA pode ser obtido que:
-
corrente de magnetização em regime permanente, sob tensão nominal: Imo =
0,2175A
reatância de dispersão do transformador: Xs = 42,845 Ω
tensão nominal primária: U1 = 13.800 Volts
O ponto no joelho da curva de saturação pode ser expresso como a magnitude em
pu da tensão de excitação para a qual a saturação se inicia. De forma típica é de 10%
acima da tensão nominal.
- tensão no transformador no ponto do joelho da saturação em pu:
Kσ = 1,1
Determinando a indutância do ramo magnetizante do transfomador a partir da
corrente magnetizante em regime permanente. Assuma que o transformador opera em
tensão nominal (1 pu).
-
freqüência da fonte: ω = 377 rad./s.
-
2
.U1
3
indutância de magnetização em Henry: Lm =
, Lm = 137,415 H
( ω.Imo )
Calcule a indutância do ar no transformador a partir da reatância de dispersão. A
indutância do ar é de 10 a 20 vezes maior que a indutância de dispersão.
Ls =
Xs
.20 , Ls = 2,273 H
ω
Cálculo o fluxo de acoplamento no joelho da curva: λ σ =
2
.U1.K σ
3
, λσ = 32,876Wb
ω
Cálculo da corrente de magnetização no joelho da curva: Imσ =
λσ
, Imσ = 0,239A
Lm
Define-se uma função de x em rampa utilizando uma função degrau. Esta função
produzirá um gráfico linearizado da característica magnética do transformador.
Φ(x) = if (x < 0,0,1)
r(x) = x . Φ(x)
Define-se a função para o fluxo. O valor da corrente de magnetização, correspondente
ao fluxo máximo não saturado, muda a característica da rampa do gráfico:
λ(x) = Lm . (r(x+Imσ) - r(x- Imσ)) + Ls .(r(-x-Imσ) - r(x- Imσ))
Desenhando-se a característica de magnetização idealizada em relação à corrente de
magnetização.
Im = -0,5, -0,45 .. 0,5 A
50
Weber
25
( )
λ Im
0
25
50
0.5
0.25
0
0.25
0.5
Im
Característica de magnetização.
Figura 3. Representação linear da saturação.
O método apresentado acima pode ser estendido para um número maior de
segmentos lineares pela inclusão de um maior número de joelhos na característica.
Entretanto, para o estudo do fenômeno da corrente de ''ínrush'', três segmentos fornecem
uma aproximação satisfatória.
A representação por segmentos lineares da característica do transformador será
utilizada abaixo para derivar a simulação do sistema.
Simulação da Energização do Transformador
Neste ítem, mostra-se um exemplo que demonstra o efeito da energização do
transformador sobre a tensão do sistema. A representação de um sistema monofásico é
utilizado para simplificar os cálculos. O leitor pode estender as equações para um
sistema trifásico.
É utilizado um método de integração numérica para se obter a solução do sistema
para o caso de energização do transformador. Por conveniência, a relação inversa entre
o fluxo e a corrente de magnetização é utilizada aqui. Portanto, definindo a corrente de
magnetização como uma função do fluxo:
Im(x) = (1/Lm). (r(x+λσ) - r(x-λσ)) - (1/Ls).(r(-x-λσ) - r(x-λσ)) - Imσ
Definindo o sistema de tensões como uma função do tempo:
φ0 = - 10 graus
U(t) =
2
.U1.cos(ω.t + φ0 )
3
O angulo de fase na função acima corresponde ao instante na forma de onda da
tensão no qual ocorre a energização do transformador. Este ângulo de fase,
juntamente com o fluxo residual, determina quão severa é a corrente de "inrush".
Definindo-se o fluxo residual no núcleo do transformador:
λo = 5 Weber
O sistema externo é representado por um equivalente RL série em série com a
tensão do sistema. Onde:
Resistência da linha: RL = 3,5Ω e reatância da linha: XL = 25Ω.
Estes valores correspondem à seguinte indutância base:
L=
XL
, L = 66 mH
ω
Considera-se um capacitor em paralelo com os terminais do transformador. Este
capacitor representa uma compensação ou é utilizado para ajustar para uma ressonância
do sistema. Assume-se então que:
-
reatância shunt capacitiva: XC = 200Ω
Correspondendo à capcitância base: C = 1/ω.XC , C = 0,1326 µF
A combinação do capacitor shunt e a indutância do sistema resulta em uma
freqüência de ressonância igual a:
fr =
1
2.π. L.C
fr = 169,71 Hz
A ressonância do sistema ocorre em uma freqüência que é próxima da freqüência
da corrente de "inrush" do transformador. Portanto, pode-se esperar na energização do
transformador uma interação harmônica entre o sistema e a não linearidade do mesmo.
O secundário do transformador é considerado aberto (sem carga). Esta
representação é preferida uma vez que resulta em cálculos pessimistas para a resposta
do sistema. A adição da carga aumentará o amortecimento do sistema e, portanto,
reduzirá de forma significativa os efeitos da corrente de "inrush".
As equações diferenciais para o sistema estão definidas a seguir.
Definindo-se as equações diferenciais do sistema.
-
derivada da corrente de linha: Di (IL , U C , t) =
(− R L .I L + UC + U(t))
L
-
derivada da tensão no capacitor: DvC (IL , U C ) =
(IL − (Im (U C ))
C
Observe que na expressão da derivada da tensão no capacitor, a saturação no
transformador é representada pela injeção da corrente de magnetização.
Define-se o passo da integração. Este passo deve ser no mínimo 10 vezes menor
que a menor constante de tempo no sistema para prevenir o aparecimento de oscilações
numéricas na solução.
ms = 0,001 s. e
dt = 0,3 ms
Define-se o tempo máximo de simulação.
T = 0,20 s.
h1 = 1,5 dt h2 = 0,5 dt
Determinando-se o número de intervalos: N = floor(T/dt)
Contando-se as interações: k = 2.. N N = 666
Definindo-se condições iniciais para o sistema:
Inicialização do tempo: t0 = 0.0 s. t1 = 0.0 s.
Calcula-se o tempo em cada intervalo: tk = k.dt
Inicializa-se a voltagem no capacitor: Uc0 = 0.0 Volts
Assume uma condição de falta no sistema antes da energização: Uc1 = 0.0 Volts
Inicializa-se a corrente de linha: i0 = 0.0 A i1 = 0.0 A
O valor inicial do fluxo no núcleo é o fluxo residual definido anteriormente.
λ0 = λo e λ1 = λo
Vectorizando as equações de estado e resolvendo o sistema de equações. A
solução fornece os valores da corrente do tranformador, da tensão no capacitor, e o
fluxo no transformador para o intervalo de cálculo.
i
 − h .D i

+ h .D i
Uc
,t
Uc
,t
 ik   (k −1) 1 i  (k −1), (k −1) (k −1)  2 i  (k −2), (k −2) (k −2)  
 Uc  

Uc(k −1) + h1.Du c i(k −1), λ (k −1)  − h 2 .Du c  i(k −2), λ(k −2) 
 k=

 λ  

 k  
λ (k −1) + h1.  Uc(k−1)  − h 2 .  Uc (k − 2) 


A resposta do sistema é mostrada abaixo.
corrente de "inrush"
10
5
( )
Im λ k
0
5
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
tk
Fig. 4. "Inrush" no transformador.
Este gráfico mostra o efeito do "offset" em cc e da característica magnética não
linear. O primeiro ciclo é severamente deslocado pela componente cc que é amortecida
em aproximadamente três ciclos.
60
50
40
Fluxo no núcleo.
30
20
λk
10
0
10
20
30
40
0
0.02
0.04
0.06
0.08
0.1
tk
Fig. 5. Fluxo no transformador.
0.12
0.14
0.16
0.18
0.2
3 .10
4
2 .10
Voltagem no barramento
4
1 .10
4
Vck
0
1 .10
4
2 .10
4
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
tk
Fig. 6. Voltagem no barramento do transformador.
No gráfico anterior, observe o efeito da corrente de "inrush" não senoidal na
voltagem do barramento. O resultado é uma sobretensão harmônica.
300
225
Corrente de linha.
150
75
ik
0
75
150
225
300
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
tk
Fig. 7. Corrente de linha.
É possível compensar alguns desses efeitos pela adição de um resistor de
pré-inserção.
0.2