Problema 3.1 Considere que uma onda de tensão triangular, com

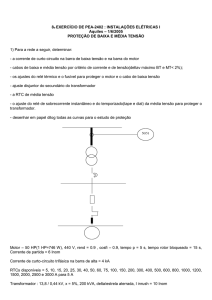
Problema 3.1
Considere que uma onda de tensão triangular, com as características indicadas na
figura, se propaga numa linha de transmissão monofásica, sem perdas e de
impedância característica Z W = 500 Ω, a partir do ponto x = 0.
u (t) [kV]
10
50 t [ µs]
1
Supondo que a linha de transmissão é infinita, represente:
a) A distribuição espacial da tensão e da corrente nos instantes de tempo t = 100 µs e
t = 200 µs.
b) A evolução temporal da tensão e da corrente no ponto x = 15 km.
Problema 3.2
Considere uma linha de transmissão sem perdas, em vazio, com 10 km de
comprimento e de parâmetros L' = 1.3 mH/km e C' = 8.6 nF/km. Na entrada da linha
está ligado um gerador cuja resistência interna é igual à impedância característica de
onda da linha.
RW
e (t)
u (x=0,t)
u (x=10 km,t)
x=0
x = 10 km
A f.e.m. do gerador tem a evolução temporal representada na figura:
e (t)
E
0
133.(3)
t [µs]
Determine a evolução temporal da tensão em x = 0 e x = 10 km, durante os primeiros
231 µs.
Problema 3.3
Considere uma linha de transmissão sem perdas, de 15 km de comprimento, com uma
impedância característica de onda Z W = 400 Ω. No instante t = 0 liga-se à entrada da
linha um gerador de f.e.m. 100 kV e resistência interna Ri = 10 Ω. A linha é terminada
por uma bobina com coeficiente de indução L = 10 mH.
t=0
Ri
L = 10 mH
e
Represente as ondas e o perfil de tensão que se observam na linha para os instantes de
tempo: t = 60 µs, t = 90 µs e t = 110 µs.
Problema 3.4
Considere uma linha de transmissão sem perdas, de 30 km de comprimento, com uma
resistência característica de onda RW = 400 Ω. No instante t = 0 liga-se à entrada da
linha um gerador de f.e.m. 100 kV e resistência interna igual à impedância
característica de onda da linha. A linha é terminada por um condensador de
capacidade C = 100 nF.
t=0
RW
e
C = 100 nF
Represente as ondas e o perfil de tensão que se observam na linha para os instantes de
tempo: t = 110 µs, t = 150 µs e t = 250 µs.
Problema 3.5
Uma linha aérea de comprimento l1 = 45 km, bifurca-se no ponto P em duas outras de
comprimentos l2 = 30 km e l3 = 15 km. As três linhas possuem características iguais,
tomando os parâmetros L' e C', por unidade de comprimento, os valores:
L' = 1.5 mH/km e C' = 7.4 nF/km.
t=0
l2
P
t=0
e2
l1
l3
e1
RW3
No instante t = 0 ligam-se à entrada das linhas l1 e l2 dois geradores e1 e e2 ,
respectivamente. O gerador e2 tem f.e.m. constante e igual a 300 kV, enquanto que o
gerador e1 possui a f.e.m. representada na figura.
e1 [kV]
150
0
250
t [µs]
Sabendo que a linha l3 se encontra adaptada, represente as ondas de tensão, que se
observam nas três linhas, nos instantes de tempo: t = 116.(6) µs; t = 166.(6) µs;
t = 216.(6) µs; t = 266.(6) µs.
Problema 3.6
Na figura representa-se um ponto de transição entre duas linhas aéreas sem perdas, de
impedâncias características Z0 ' = 250 Ω e Z0 '' = 500 Ω, no qual se montou em
derivação uma capacidade C.
ui
P
Z0 '
u
C
Z0 ''
Suponha que no ponto P incide uma onda de tensão, proveniente de uma descarga
atmosférica, dada por:
(
u i (t ) = U e − t τ1 − e − t τ 2
)
onde U = 1 MV, τ1 = 71.4 µs e τ2 = 0.17 µs. Nestas condições, determine a evolução
da tensão no ponto P, considerando que a capacidade toma os valores:
a)
C = 0.01 µF.
b)
C = 0.1 µF.
Problema 3.7
Uma descarga atmosférica, com as características indicadas na figura, propaga-se
numa linha aérea sem perdas de 30 km de comprimento, na extremidade da qual está
ligado um transformador.
u [kV]
600
300
50 t [µs]
2
a)
Determine o valor máximo da tensão que atinge o transformador, sabendo que
o dispositivo limitador de sobretensões, colocado a 300 m do transformador,
tem a característica u(i) apresentada na figura.
u [kV]
150
i
-150
b)
Suponha agora que o mesmo dispositivo limitador de sobretensões está
colocado a 10 m do transformador. Determine o valor máximo da tensão que
atinge o transformador.
Problema 3.8
Considere a ocorrência de um curto-circuito aos terminais de um disjuntor de linha,
ligada a um barramento de 30 kV de uma subestação. A rede a montante, cujo
esquema monofásico equivalente se representa na figura, é caracterizada pela sua
potência de curto-circuito Scc = 750 MVA e pela frequência natural fn = 10 kHz.
t=0
L
~
2
1
C
vr
Calcule o valor de pico e a taxa de crescimento da TTR, considerando:
a) Corte com corrente nula.
b) Corte com supressão da corrente com o valor -2 kA.
Problema 3.9
Considere a rede do problema anterior. Determine o valor da resistência a colocar em
paralelo com o disjuntor de forma a assegurar um regime aperiódico limite. Para esta
situação, e considerando o corte com corrente nula, determine a expressão da TTR e a
respectiva taxa de crescimento máxima.
Problema 3.10
Considere a rede do problema 3.8 e suponha que o curto-circuito se dá na linha (cuja
reactância é 0.4 Ω/km), à distância de 2 km da subestação.
Calcule o valor da TTR aos terminais do disjuntor, para o corte com corrente nula,
bem como a respectiva taxa de crescimento.
Problema 3.11
Num barramento de uma rede 60 kV, com potência de curto-circuito de 1500 MVA e
relação Xs/Rs=3 pode ser ligada uma bateria de condensadores com a potência
nominal de 15 Mvar por meio de um disjuntor.
Ls
Rs
D
vr
v (t)
Cs
~
C
vc
Desprezando a capacidade equivalente da rede, calcule:
a) O valor de pico da corrente de ligação da bateria de condensadores.
b) A tensão a que fica carregada a bateria de condensadores após o primeiro
reacendimento do arco no disjuntor, quando se abre o disjuntor.
Problema 3.12
Considere o equivalente monofásico de uma rede de 60 kV caracterizada pela sua
potência de curto-circuito no barramento 1 Scc = 1500 MVA e pela frequência natural
fn = 8 kHz.
t=0
L1
2
1
~
C1
V1
Vr
C2
V2
L2
No barramento 2 está ligado um transformador em vazio de potência nominal
SnT = 75 MVA e com uma capacidade distribuída representada pelo condensador
C2 = 100 nF. Considere que o transformador é desligado com supressão da corrente
máxima.
a) Determine os parâmetros L1 e C1 da rede a montante do disjuntor. Sabendo que a
corrente de magnetização é 5% da corrente nominal, calcule o parâme tro L2 capaz de
representar o transformador em vazio.
b) A evolução da tensão v1 , calculando os parâmetros que a caracterizam.
c) A evolução da tensão vr, calculando os parâmetros que a caracterizam.