Evitamento de Chattering no controle Backstepping Sliding

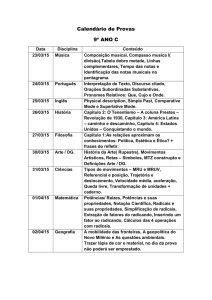
Evitamento de Chattering no controle Backstepping Sliding-Mode de veículos
subaquáticos autônomos para inspeção de barragens
Glauco Ércico Rocha da Silva(PIBIC/Fundação Araucária/Unioeste), Carlos
Henrique Farias dos Santos(Orientador), e-mail: [email protected]
Universidade Estadual do Oeste do Paraná/Centro de Engenharias e Ciências
Exatas/Foz do Iguaçu, PR.
Engenharias - Engenharia Naval e Oceânica
Palavras-chave: Backstepping Sliding Mode Control, Veículos Subaquáticos,
Automação de Sistemas Propulsores
Resumo
Este artigo tem como proposito apresentar resultados referentes a implementação
da técnica Backstepping Sliding Mode Control com o objetivo de evitar o fenômeno
Chattering responsável por perdas de calor nos sistemas elétricos e fadiga dos
componentes mecânicos dos AUV’s (Autonomus Underwater Vehicles). Foi
implementada esta técnica no bloco referente à estabilização do AUV na superfície
de deslizamento modelada previamente.
Introdução
Na Teoria de Estruturas Variáveis de Sistemas as entradas de controle
tomam como valores os limites extremos de retransmissão de um grupo, pré
especificado, de funções de controle de realimentação. A lógica comutada é
desenvolvida para atuar comandando a malha fechada de um sistema dinâmico que
permite estabilidade (Edwards & Spurgeon, 1998; Antonelli, 2006; Perruqueti &
Barbot, 2009). Baseada nesses princípios, foi desenvolvida uma técnica de controle
popularizada por Utkin (1993): Controle por Modos Deslizantes. Esta técnica pode
ser aplicada a veículos não tripulados, os quais podem ser projetados para atuar no
ar, na terra e em ambientes aquáticos. No presente trabalho, desenvolve-se um
estudo levando em consideração as operações de monitoramento de barragens
utilizando os veículos não tripulados subaquáticos (Chiella, 2012), chamados de
AUV’s (Autonomous Underwater Vehicles), do qual difere dos ROV’s (Remotely
Operated Vehicles), classe de veículos subaquáticos na qual há intervenção humana
por meio de controle remoto.
O Controle por Modos Deslizantes (SMC) pode ser considerado um caso
particular das técnicas de Controle Não-Linear (Fossen, 1994; Khalil, 2002; Choi &
Kondo, 2010; Fossen, 2011). Sua principal característica é que, uma vez alcançado
o estado desejado previamente, este se torna insensível a parâmetros da planta e
interferências externas. Para lidar com a correção do fenômeno Chattering,
intrínseco à estratégia por Modos Deslizantes, neste trabalho é proposta uma
solução para este problema, implementando uma abordagem Backstepping sobre a
técnica por Modos Deslizantes (Liu & Wang, 2012), auxiliada por uma função
hiperbólica. A lei de controle é desenvolvida com o objetivo de alcançar e manter
estável a superfície.
Material e Métodos
Neste trabalho, primeiramente, foi feito um estudo de técnicas de controle
linear e não linear. Depois, foi feito um estudo no software MATLAB/Simulink, uma
vez que este foi necessário para fazer as simulações do AUV tendo implementado a
técnica Backstepping Sliding Mode no código de simulação referente aos
propulsores do AUV.
Resultados e Discussão
Tendo em vista o vetor erro de posição: ῆ= η – ηd, onde η(6x1) é o vetor de
posição atual do AUV e ηd(6x1) é o vetor de posição desejada do AUV; temos
também o vetor erro velocidade: ṽ= ν – νd, onde ν(6x1) é o vetor de velocidade atual e
νd(6x1) é o vetor de velocidade desejado do AUV.
A seguir estão representados, respectivamente, a matemática referente as
matrizes de transformação J(6x6)(η) de velocidade desejada, a matriz de Coriolis
C(6x6)(ν), o vetor de velocidade atual em relação ao referencial estático do corpo
νr(6x1), e o vetor de velocidade virtual em relação ao referencial estático do corpo
νre(6x1) (Chiella, 2012; Cildoz, 2014),:
J(η) =
(1)
C(ν) = CA(ν) + CRB(ν)
νr = Kp·ῆ + Kd·ṽ + Ki·∫ῆ
νre = J(η)-1· νr
(2)
(3)
(4)
onde J1(3x3)
é a matriz de velocidade linear, J2(3x3)
é a matriz de transformação
de velocidade angular, CA(6x6)(ν) é a matriz de massas adicionais, CRB(6x6)(ν) é matriz
de Coriolis rígida ao corpo, ∫ῆ(6x1) é o vetor de erros integrais com Kp > 0, Kd· > 0 e
Ki > 0 (nesse trabalho foi adotado Kp = 35, Kd = 10 e Ki = 80).
Na ordem de demonstrar a estabilidade do controlador, selecionamos a
função de Lyapunov como V1 =
V1'
. Visto que s = ν – νd + c1.ῆ = ṽ + c1.ῆ, para realizar
0, tem-se que:
V1' = ῆ.ῆ' = ῆ.ṽ = ῆ.(s - c1.ῆ) = ῆ.s - c1.ῆ2
0
(5)
onde s é a superfície de deslizamento e c1 > 0 (nesse trabalho foi adotado c1 = 1.2).
Se s = 0, V1' 0. Tendo que s' = ṽ' + c1.ῆ' = Ṅ + M. + c1.ῆ' - ad, onde M(6x6) é a matriz
inercial e ad(6x1) é o vetor de aceleração desejada do AUV, Ṅ = [C(6x6)(ν) +
D(6x6)(ν)]·νre(6x1) + G(6x6)(η), sendo D(6x6)(ν) é matriz de amortecimento hidrodinâmico,
G(6x6)(η) é a matriz de restauração e selecionando uma função de Lyapunov
diretamente em função de s, V2 = V1 + , tem-se que a derivada de V2 é:
V2' = V1' + s.s'.
Para que V2'
seguir:
(6)
0 seja satisfeito, o controlador deve ser desenvolvido como a
= – Ṅ – M-1·[νre + c2·s + ῆ + c1·ṽ – ad + ζ·tanh(s)]
(7)
onde c2 > 0 e ζ > 0 (nesse trabalho foi adotado c2 = 30 e ζ = 100). Fazendo s ⟶ 0 e
ῆ ⟶ 0 quando t ⟶ ∞, temos que V2'
Figura 1 – trajetória do AUV
0 e a condição de estabilidade é satisfeita.
Figura 2 – Erros de trajetória
Figura 3 – Propulsores
Figura 4 – Superfície do AUV
A Figura 1 mostra a trajetória de 65 metros percorrida pelo AUV em 720
segundos. A Figura 2 exibe os erros de trajetória nas seis coordenadas, os quais
representam o resultado satisfatório. A Figura 3, mostra o esforço dos propulsores,
onde não ocorre o fenômeno do Chattering, e finalmente, a Figura 4 mostra as
superfícies de controle nos cinco graus de liberdade controlados. Neste último fica
evidente que ocorre a convergência para zero, como esperado.
Conclusões
Através dos gráficos gerados após a simulação da trajetória do AUV,
podemos comparar a técnica Backstepping Sliding Mode auxiliada por função
hiperbólica com outras abordagens Sliding Mode (Cildoz, 2014). Aplicada na lei de
controle, é visto que o fenômeno Chattering é reduzido grandemente, tendo sido
reduzido satisfatoriamente o erro durante a trajetória, garantindo maior estabilidade
do AUV.
Outra vantagem da aplicação desta técnica é que os esforços dos propulsores
também são reduzidos, evitando problemas de superaquecimento e fadiga nos
sistemas elétrico e mecânico, respectivamente. Com isso é possível ter um gasto
energético menor e uma vida útil maior para esse, economizando nos gastos com a
manutenção do veículo.
Como visto, ao se usar a técnica Backstepping Sliding Mode é garantido um
desempenho satisfatório no comportamento do AUV, visto que ocorre um equilíbrio
entre desempenho, estabilidade e economia energética.
Agradecimentos
Ao Programa Institucional de Bolsas de Iniciação Tecnológica
PIBIC/Fundação Araucária pela concessão de bolsa de iniciação científica.
-
Referências
Antonelli, G. (2006). Underwater Robots, Motion and Force Control of VehicleManipulator Systems, Springer tracts in advanced robotics. Berlim: Springer-Verlag
Berlin Heidelberg.
Chiella, A. (2012). Control Strategies Applied to Autonomous Underwater Vehicle for
Inspection of Dams. In 12th Pan American Congress of Applied Mechanics, Porto de
Espanha, Trinidad e Tobago.
Choi, J-K.; and Kondo, H. (2010). On Fault-Tolerant Control of a Hovering AUV with
Four Horizontal and Two Vertical Thrusters. In OCEANS 2010 IEEE, Sydney,
Australia.
Cildoz, M. (2014). Comparative Study of Chattering-Free Sliding Mode Controllers
Applied to an Autonomous Underwater Vehicle (AUV). In 11th Portuguese
Conference on Automatic Control, Porto, Portugal.
Edwards, C. & Spurgeon, S.K. (1998). Sliding Mode Control: Theory and
Applications. Boca Raton: CRC Press.
Fossen, T.I. (1994). Guidance and Control of Ocean Vehicles. Nova Jersey: Wiley.
Fossen, T. I. (2011). Handbook of Marine Craft Hydrodynamics and Motion Control.
Nova Jersey: Wiley.
Khalil, H. (2002). Nonlinear Systems. Nova Jersey: Prentice Hall.
Liu, J. & Wang, X. (2012). Advanced Sliding Mode Control for Mechanical Systems:
Design, Analysis and MATLAB Simulation. Berlim, Springer-Verlag Berlin Heidelberg.
Perruqueti, W. & Barbot, J.P. (2002). Sliding Mode Control in Engineering. Nova
York: Marcel Dekker Inc.
Utkin, V. (1993). Sliding Mode Control Design Principles and Applications to Electric
Drives. IEEE Transactions of Industrial Eletronics 40, 23-36.
Utkin, V. (2009). Sliding Mode Control in Electro-Mechanical Systems. Boca Raton:
CRC Press.