LISTA DE EXERCÍCIOS DO MÓDULO 22 – Resolução de

Matemática
A/B
2º
3º
Luiz Carlos Fontenelle Neto
X
1,0
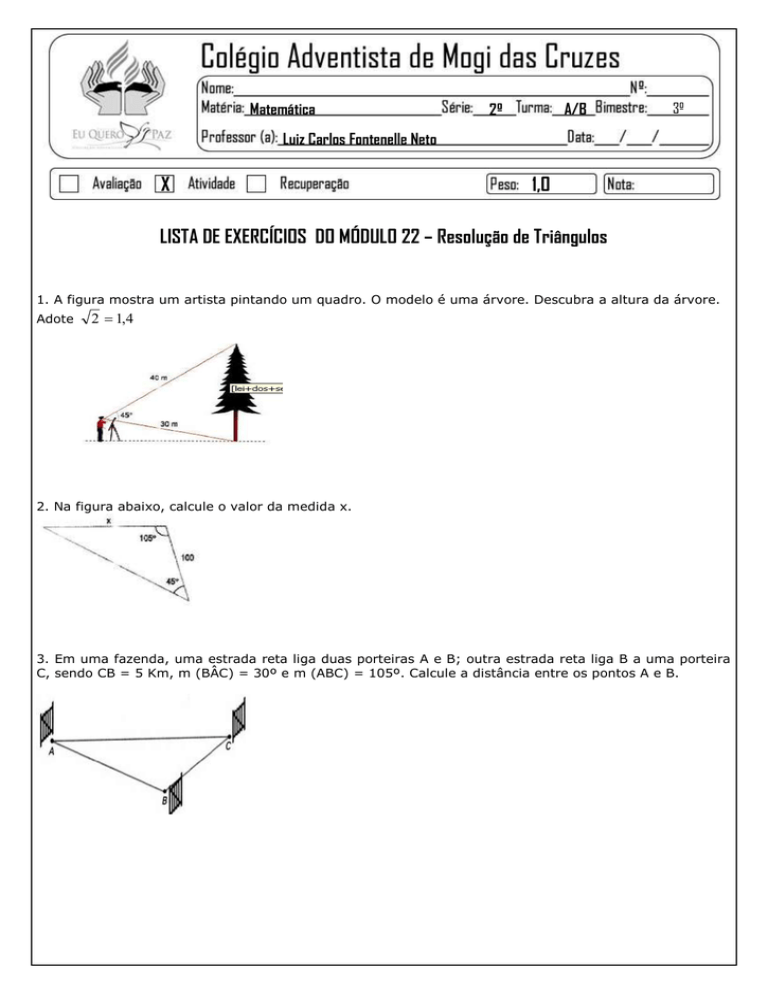
LISTA DE EXERCÍCIOS DO MÓDULO 22 – Resolução de Triângulos
1. A figura mostra um artista pintando um quadro. O modelo é uma árvore. Descubra a altura da árvore.
Adote
2  1,4
2. Na figura abaixo, calcule o valor da medida x.
3. Em uma fazenda, uma estrada reta liga duas porteiras A e B; outra estrada reta liga B a uma porteira
C, sendo CB = 5 Km, m (BÂC) = 30º e m (ABC) = 105º. Calcule a distância entre os pontos A e B.
4. Uma ponte deve ser construída num rio, unindo os pontos A e B, como ilustrada na figura abaixo. Para
calcular o comprimento AB, escolhe-se um ponto C, na mesma margem em que B está, e medem-se os
ângulos CBA = 57º e ACB = 59º. Sabendo que BC mede 30 m, indique, em metros, a distância AB. ( Use
as aproximações sen 59º = 0,87 e sen 64º = 0,90.
5. Um topógrafo pretende medir a distância entre dois pontos (A e B) situados em margens opostas de
um rio. Para isso, ele escolheu um ponto C na margem em que está e mediu os ângulos ACB e CAB,
encontrando, respectivamente, 45º e 60º e que o lado AC mede 16 m, respeitando essas condições,
podemos afirmar que o lado AB tem medida aproximadamente de: Use se necessário sem 75º = 0,96,
cos 75º = 0,25 e tg 75º = 3,73.
6. No triângulo da figura abaixo, determine a medida a.
7. No triângulo da figura abaixo, são dados: a = 6, b = 4 e C = 60º. Calcule a medida c.
8. (Unicamp) - A água utilizada na casa de um sítio é captada e bombeada do rio para uma caixa d´água
a 50 m de distância. A casa está a 80 m de distância da caixa d´água e o ângulo formado pelas direções
caixa d´água – bomba e caixa d´água – casa é de 60º. Se a idéia é bombear água do mesmo ponto de
captação até a casa, quantos metros de encanamento são necessários?
9. Para saber o comprimento de uma ponte que será construída sobre um rio, um engenheiro instalou o
teodolito no ponto B a uma distância de 30 metros do ponto A, situado na margem do rio. Depois, mediu
os ângulos BAC = 105º e CBA = 30º. Conforme a figura. Com base nas medidas feitas pelo engenheiro,
determine o comprimento AC da ponte.
10. Determine a medida x indicada no triângulo acutângulo abaixo:
A
60º
8 cm
45º
B
C
x
11. Determine o valor de x no triângulo abaixo:
x
6 cm
60º
8 cm
12. Num triângulo ABC, o ângulo  mede 60º e o lado oposto mede 7 cm. Se um dos lados adjacentes ao
ângulo  mede 3 cm, qual a medida do outro lado do triângulo?
A
3 cm
B
7 cm
C
13. Utilizando a lei dos cossenos no triângulo ABC, determine o valor de x:
x
3 cm
60º
4 cm
14. (FEI – SP) No triângulo da figura. O valor do cos
a)
b)
c)
d)
e)

é:
6
12
3
2
1
2
6
4
2 6
3
15. (FGV – SP) Qual a área do triângulo abaixo?
a)
b)
c)
d)
e)
6 cm 2
6 2cm 2
4 2cm 2
8 2cm 2
10 cm 2
16. (UFAL) A área, em centímetros quadrados, do triângulo representado na figura abaixo é:
a)
40 2
b) 20 3
c) 20 2
d) 25
e) 10
17. (USF – SP) Examine a Figura
A área do triângulo ABC representado é em cm2:
a) 60
b) 30
c) 17
d) 15
e) 18,5
18. Duas forças de intensidade F1 = 8 N e F2 = 12 N formam entre si um ângulo de 120º. Qual a
intensidade R da resultante dessas duas forças?
19. (UERJ) Um triângulo tem lados 3, 4 e 5. A soma dos senos dos seus ângulos vale:
a) 1,4
b) 1,5
c) 1,8
d) 2
e) 2,4
20. (UECE) Na figura , MNPQ é um trapézio isósceles, MN = 20 cm, QP = 10 cm e θ = 60º. Então, a área
desse trapézio, em centímetros quadrados, é:
a)
55 3
b)
65 3
c)
75 3
d)
85 3
Boa Lista !!!