FAP151-Fundamentos de Mecânica - Plato

FAP151-Fundamentos de Mecânica.
Lista 4
Revisão de Vetores
Este assunto está no livro do Halliday, capítulo 2 ou 3, conforme você tiver a 5a ou 4a edição,
respectivamente. Tente solucionar as questões abaixo. Caso encontre facilidade em resolvê-las, pode
seguir adiante. Caso encontre dificuldade, leia o texto compreendido entre as páginas 185 a 196 do livro
Física 1 - mecânica, do GREF, Editora da USP, 1990, e retorne a estes exercícios.
12
10
8
y
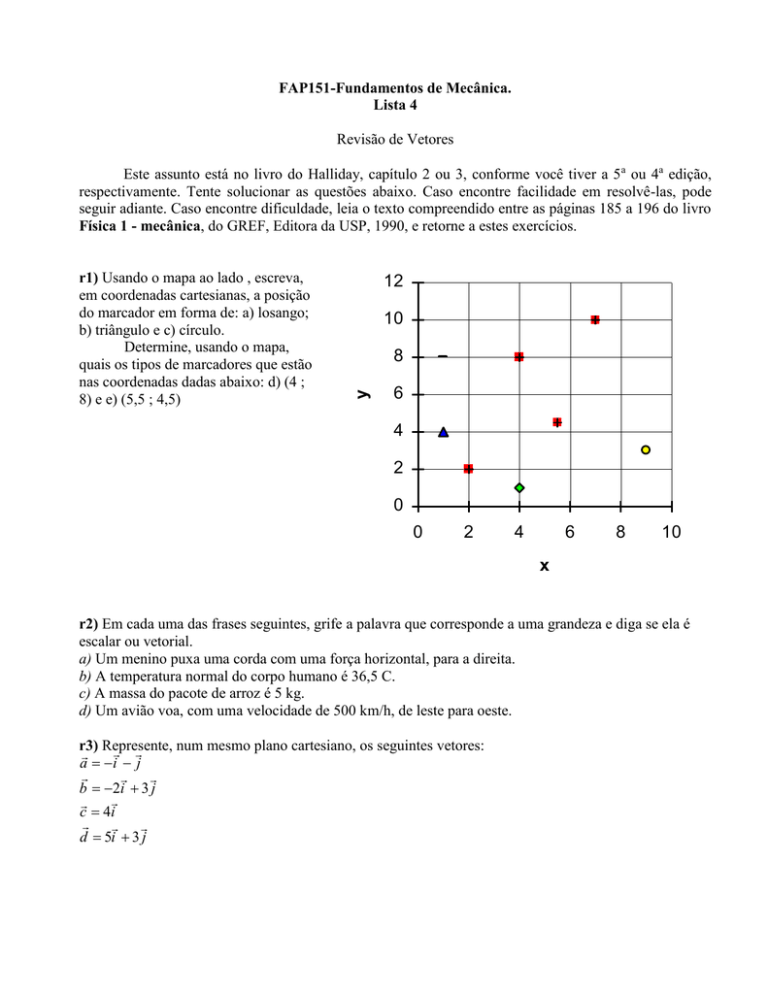
r1) Usando o mapa ao lado , escreva,
em coordenadas cartesianas, a posição
do marcador em forma de: a) losango;
b) triângulo e c) círculo.
Determine, usando o mapa,
quais os tipos de marcadores que estão
nas coordenadas dadas abaixo: d) (4 ;
8) e e) (5,5 ; 4,5)
6
4
2
0
0
2
4
6
8
10
x
r2) Em cada uma das frases seguintes, grife a palavra que corresponde a uma grandeza e diga se ela é
escalar ou vetorial.
a) Um menino puxa uma corda com uma força horizontal, para a direita.
b) A temperatura normal do corpo humano é 36,5 C.
c) A massa do pacote de arroz é 5 kg.
d) Um avião voa, com uma velocidade de 500 km/h, de leste para oeste.
r3) Represente,
num mesmo plano cartesiano, os seguintes vetores:
 

a  i  j



b   2i  3 j


c  4i



d  5i  3 j
r4) Escreva, usando coordenadas cartesianas, cada um dos vetores representados abaixo:
2
b
d
y
c
1
e
a
-3
-2
O
-1
1
2
x
3
f
-1
i
j
g
h
k
-2
EXERCÍCIOS
Para entregar, Exercícios 4 e 10.
Vetores
1) (RHK E.2 2.1Considere dois deslocamentos, um com 3 m de intensidade e outro com 4 m. Mostre
como os vetores deslocamentos podem ser combinados para dar um deslocamento resultante de
intensidade a) 7 m, b) 1 m e c) 5 m.
2) Utilizando os vetores a= 1xi + 3yj + 2zk, b= -1yj + 4zk e c= 3xi – 4yj – 1zk, determine
a) a+b+c;
b)
|a + c| e
c)
|a – 2b|.

 
3) a) Qual é a soma, usando a notação dos vetores unitários dos dois vetores a  5 i  3 j e



 
b   3 i  2 j ? b) Qual é a intensidade e a direção de a  b ?



a  2i  4 j



4) Sejam os vetores: b  2i  2 j


c  2i
Represente graficamente os seguintes vetores, utilizando um papel quadriculado, e escreva as suas
representações
analíticas:
 
a) a  b
 
b) a  c
 
c) a  b
 
d) c  b






5) Dados dois vetores A  4,00i  3,00 j e B  5,00i  2,00 j : a) ache o módulo, direção e sentido de
  
cada vetor; b) escreva uma expressão para a diferença vetorial C  A  B usando vetores unitários; c)

ache o módulo, a direção e o sentido de C ; d) represente os vetores em um diagrama em escala e mostre
que os resultados obtidos a partir de medições no diagrama concordam com os do item c.
6) Uma espeleóloga está pesquisando uma caverna. Ela percorre 180 m em linha reta de leste para o
oeste, depois caminha 210 m em uma direção formando 45º com a direção anterior e em sentido do sul para o
leste; a seguir, percorre 90 m a 30º no sentido do norte para o oeste. Depois de um quarto deslocamento não
medido, ela retorna ao ponto de partida. Use um diagrama em escala para determinar o módulo, a direção e o
sentido do quarto deslocamento.
7) Determine o módulo, a direção e o sentido dos vetores representados pelos seguintes ares de
componentes:
a) Ax = -8,60 cm, Ay = 5,20 cm; b) Ax = -9,70 m, Ay = - 2,456 m;
c) Ax = 7,75 km, Ay = -2,70 km.



 

8) (RHK E2.9) Dados dois vetores, a  4,0i  3,0 j e b  6,0i  8,0 j , determine as intensidades e as

 
 
 

direções (avaliadas a partir do sentido positivo do eixo x) de a) a , b) b , c) a  b , d) a  b , e) b  a .


  
 

 
 
9) Dois vetores são dados por a  4i  3 j  k e b  i  j  4k . Determine a) a  b , b) a  b , c) um
  

vetor c tal que a  b  c  0 .
10) Um pombo correio é solto em um ponto A e é observado ao longo de seu vôo. Ele voa 10 km para o
sul e, então, percorre 15 km para o leste. Posteriormente, voa 10 km para o sudeste e, finalmente, 5 km
para o sul até atingir seu destino em B. Determine graficamente a mínima distância entre A e B.
Despreze a curvatura da terra.