Teoria da Probabilidade Espaço de Amostras Espaço de Amostras

Departamento de Informática
Disciplina: Modelagem Analítica do
Desempenho de Sistemas
de Computação
Medida de Probabilidade
Teoria da Probabilidade
Modelagem Analítica
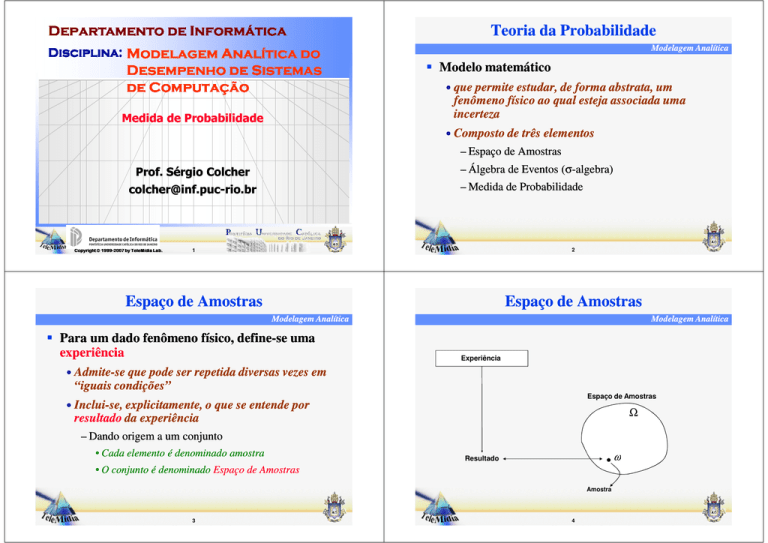
Modelo matemático
• que permite estudar, de forma abstrata, um
fenômeno físico ao qual esteja associada uma
incerteza
• Composto de três elementos
– Espaço de Amostras
– Álgebra de Eventos ((σ
σ-algebra)
Prof. Sérgio Colcher
– Medida de Probabilidade
[email protected]
1
2
Espaço de Amostras
Espaço de Amostras
Copyright  19991999-2007
2007 by TeleMídia Lab.
Modelagem Analítica
define-se uma
Para um dado fenômeno físico, defineexperiência
Modelagem Analítica
Experiência
• Admite
Admite--se que pode ser repetida diversas vezes em
“iguais condições”
Espaço de Amostras
• Inclui
Inclui--se, explicitamente, o que se entende por
Ω
resultado da experiência
– Dando origem a um conjunto
• Cada elemento é denominado amostra
ω
Resultado
• O conjunto é denominado Espaço de Amostras
Amostra
3
4
Álgebra de Eventos
Espaço de Amostras: Algumas Considerações
Modelagem Analítica
É possível definir subconjuntos de Ω e inquirir se
o resultado da experiência pertence a um desses
subconjuntos.
• Se definidos de forma adequada, esses subconjuntos
Eventos..
são denominados Eventos
– A cada evento associaremos uma medida de
probabilidade, logo
• Eventos devem ser “complementares”, no sentido de
que, unidos, formam todo o espaço
Modelagem Analítica
Quando jogamos uma moeda, sabemos ser possível ela cair “de pé”
• Mesmo assim costumamos ignorar essa situação
No experimento de tomar a idade de uma pessoa (como um número
inteiro de anos completados), o espaço de amostras é finito ?
• É razoável achar que uma pessoa pode chegar a 1000 anos ?
– De acordo com fórmulas extraídas das tabelas de mortalidade, a
proporção de seres humanos sobrevivendo até 1000 anos é da ordem de
1 a cada 1010
36
(um número com 1027 bilhões de zeros)
• Se 1010 pessoas nascessem por século, seriam necessários
35
1010 séculos para encontrarmos uma pessoa que vive 1000 anos.
– Isso é mais do que
1010
34
vidas do planeta terra.
5
6
Álgebra de Eventos
Propriedade das Álgebras
Modelagem Analítica
Uma coleção de eventos (conjuntos) A (denominada
classe) é uma Álgebra quando satisfaz as seguintes
classe)
condições
•
Se A é uma álgebra então
i)
i) A ∈ A ⇒ A ∈ A
ii)
Modelagem Analítica
A∈ A
 ⇒ A∪ B∈ A
B ∈ A
Diz-se que a classe A é fechada em relação às operações
Dizde complemento e união
10
A∈ A
 ⇒ A∩ B∈ A
B ∈ A
A∈ A
 ⇒ B − A∈ A
B ∈ A
iii) ∅ ∈ A, Ω ∈ A
ii)
11
Álgebra de Eventos
Espaço de Amostras
Modelagem Analítica
Uma classe é fechada em relação às operações de
• União, interseção, complemento e diferença
Por indução, é possível mostrar que a união de
um número qualquer finito de eventos também é
um evento
Modelagem Analítica
Finito x Infinito
Discreto x Contínuo
• Discreto quer dizer “contável” ou “enumerável”
Infinito não quer dizer necessariamente contínuo.
Discreto não quer dizer necessariamente finito.
12
13
Conjunto Contável
σ- Álgebra
Modelagem Analítica
Um conjunto é contável quando é possível
estabelecer um mapeamento “um“um-para
para--um” entre
seus elementos e o conjunto dos números inteiros
positivos.
Modelagem Analítica
Uma álgebra é uma σ- Álgebra quando satisfaz à
seguinte condição
∞
Ai ∈ A ; i = 1,2 ,... ⇒ U Ai ∈ A
i =1
14
15
Medida de Probabilidade
Medida de Probabilidade
Modelagem Analítica
Procura modelar a “freqüência relativa” de um
evento associada a uma experiência.
• Assuma que se tenha observado um fenômeno N
vezes. Destas N vezes, anotaanota-se o número de vezes
que um dado evento A tenha ocorrido. Representado
este número por n(A), a razão n(A)/A é a freqüência
relativa de ocorrência de A para as N observações.
– A freqüência relativa é um valor entre 0 e 1.
– A freqüência relativa associada ao evento Ω é igual a 1
Modelagem Analítica
Seria possível pensar em definir a probabilidade
P(A) associada a um determinado evento A como
n( A)
lim
?
N →∞ N
• Embora definir a medida de probabilidade dessa
forma seja, a primeira vista, atraente, esbarraesbarra-se em
uma série de argumento práticos.
• Utiliza
Utiliza--se uma definição mais pragmática, baseada
em uma série de axiomas denominados de axiomas
da probabilidade
16
17
Funções Conjunto Finitamente Aditivas
Funções Conjuto
Modelagem Analítica
Os Axiomas de Probabilidade são baseados em
entidades matemáticas conhecidas como
• “Funções Conjunto Finitamente Aditivas”
Aditivas” e
Modelagem Analítica
Funções em que
• O domínio é uma álgebra
• O contracontra-domínio é formado por valores reais
• “Funções Conjunto Contavelmente Aditivas”
Aditivas”
18
19
Funções Conjunto Finitamente Aditivas
Funções Conjunto Finitamente Aditivas
Modelagem Analítica
Modelagem Analítica
Exemplos
Uma função conjunto f : A → R é dita finitamente aditiva se
f ( A ∪ B ) = f ( A) + f ( B)
sempre que A e B são conjuntos disjuntos pertencentes a A.
• Área
• Comprimento
• Massa
• ...
20
21
Teorema da União
Função Conjunto Contavelmente Aditiva
Modelagem Analítica
Se f é finitamente aditiva então :
f ( A ∪ B) = f ( A) + f ( B) − f ( A ∩ B)
Prova:
Ω
=A
A∩B
A
Modelagem Analítica
Uma função conjunto f : A → R é dita contavelmente aditiva se
∞
∞
k =1
k =1
f U Ak = ∑ f ( Ak )
sempre que Ai ∩ A j = ∅ e i ≠ j.
A∩ B
B
A ∪ B = A ∪ ( A ∩ B)
f ( A ∪ B) = f ( A) + f (A ∩ B )
B = ( A ∩ B) ∪ ( A ∩ B)
f ( B ) = f ( A ∩ B ) + f (A ∩ B )
A álgebra A deve ser uma σ- Álgebra
f ( A ∪ B) = f ( A) + f ( B ) − f ( A ∩ B )
22
23
Axiomas da Probabilidade
Propriedades da Probabilidade
Modelagem Analítica
A Medida de Probabilidade é definida simplesmente
como uma função em A que obedece aos seguintes
três axiomas
• Axioma 1: P(A) ≥ 0
• Axioma 2: P(Ω ) = 1
Função Conjunto
Finitamente Aditiva
• Axioma 3:
Modelagem Analítica
Aditividade
Complemento
Probabilidade do Evento Vazio
Limitante superior
União
(a) Se A ∩ B = ∅, então P ( A ∪ B ) = P ( A) + P ( B )
∞
∞
i =1
i =1
(b) Se Ai ∩ A j = ∅; i, j = 1,2,... (i ≠ j ), então P( U Ai ) = ∑ P( Ai )
Função Conjunto
Contavelmente Aditiva
24
25
Propriedade da Aditividade
Propriedade do Complemento
Modelagem Analítica
{Ai}, i =
Para uma coleção de n eventos disjuntos {A
1, ..., n, isto é
Ai I A j = ∅; i = 1,..., n (i ≠ j )
Modelagem Analítica
P( A ) = 1 − P( A)
Prova: a partir da definição de complemento, tem-se que
A∪ A = Ω
resulta que
n  n
P U Ai  = ∑ P( Ai )
 i =1  i =1
Utilizando o axioma 3(a) e o axioma 2:
(Prova: por indução)
P ( A) + P ( A ) = P (Ω) = 1
P ( A ) = 1 − P ( A)
26
27
Propriedade da Probabilidade do Evento Vazio
Propriedade do Limitante Superior
Modelagem Analítica
Modelagem Analítica
P(∅) = 0
P( A) ≤ 1
Prova: o complemento de ∅ é Ω , portanto
Prova:
P(∅) = 1 − P(Ω)
P( A) + P ( A ) = 1
Pelo axioma 2, P(Ω
Ω ) = 1. Logo
como, pelo axioma 1, P(A ) ≥ 0,
1 é um limitante superior para P ( A).
P(∅) = 0
28
29
Propriedade da União
Probabilidade Condicional
Modelagem Analítica
P ( A ∪ B ) = P ( A) + P ( B ) − P ( A ∩ B )
Suponha uma população com N indivíduos
Suponha dois eventos
Prova:
Ω
=A
Modelagem Analítica
• A: o indivíduo é do sexo feminino
A∩B
• B: o indivíduo é daltônico
Pode
Pode--se definir as probabilidades
A
A∩ B
B
A ∪ B = A ∪ ( A ∩ B)
P( A ∪ B ) = P ( A) + P (A ∩ B )
B = ( A ∩ B) ∪ ( A ∩ B)
P( B) = P( A ∩ B ) + P(A ∩ B )
• P(A) = Nf / N
• P(B) = Nd / N
Poderíamos estar interessados em saber a probabilidade
de se ser daltônico dentro da população feminina.
• ou seja: P(B|A) = Nfd / Nf
• dividindo os dois lados por N
P ( B | A) =
P( A ∪ B ) = P( A) + P( B) − P( A ∩ B )
30
31
P( A ∩ B )
P( A)
Probabilidade Condicional
Probabilidade Condicional
Modelagem Analítica
Dados dois eventos A e B, desejamos modelar a
probabilidade de ocorrência do evento B dado
que sabemos que o evento A ocorreu: P(B | A).
• Em outras palavras, queremos a freqüência relativa
do evento A∩
A∩B em relação ao evento A
Modelagem Analítica
Definição
• Dados dois eventos A e B, com P(A) > 0, chamachama-se
P(B | A) a probabilidade condicional de B dado A
(ou probabilidade de B condicionada a A)
A) definida
pela expressão
– Queremos uma medida que modele
P( B | A) =
n( A ∩ B )
N
n( A)
N
n( A ∩ B )
=
n( A)
P( A ∩ B)
P ( A)
32
33
Probabilidade Condicional
Probabilidade Condicional
Modelagem Analítica
• Obviamente, se A e B são disjuntos então
Modelagem Analítica
• Se B ⊂ A
B
P(B | A) = 0
A
B
P(B | A) = P(B)/P(A)
A
• Se A ⊂ B
• Caso geral
B
P(B | A) = 1
B
A
P( B | A) =
A
A∩ B
34
35
P( A ∩ B)
P( A)
Exemplo Utilizado em Caltech
Exemplo Utilizado em Caltech
Modelagem Analítica
Cada aluno foi instruído a listar o número de
filhos homens e mulheres de sua família.
Resultado: o número de homens é maior
Modelagem Analítica
• Aproximadamente 2/3
– Detalhe: todos os alunos eram homens.
É possível inferir estatisticamente que a
população masculina é maior do que a população
feminina no estado ?
A estatística obtida não é a probabilidade de um filho ser homem naquela
população e sim a probabilidade do filho ser homem dado que ele vem de
uma família com pelo menos um filho homem
Considere, por exemplo, um espaço amostral composto por 4n
4n famílias,
cada uma com 2 filhos, totalizando 8n filhos da seguinte forma:
• n famílias tem dois filhos homens,
• 2n famílias tem um homem e uma mulher e
• n famílias tem 2 filhas mulheres.
Considere os eventos:
• A = “filho é homem”
homem” e
• B = “família tem pelo menos um filho homem”
• Tem
Tem--se que
– P(A) = 0,5
– P(B) = 33n
n/4n
/4n = 3/4
P( A | B ) =
P ( A ∩ B ) P ( A) 1 2 2
=
=
=
P( B)
P( B) 3 4 3
36
37
Independência Entre Dois Eventos
Independência Entre Dois Eventos
Modelagem Analítica
Dois eventos A e B são estatisticamente
independentes quando
P( A ∩ B) = P( A) ⋅ P( B)
Modelagem Analítica
A noção de independência é particularmente
importante quando P(A) e P(B) são ambos
maiores do que zero
• Nessas condições, resulta imediatamente da
definição de probabilidade condicional que cada
uma das condições a seguir é equivalente à
definição de independência
P ( B | A) = P( B)
P ( A | B) = P( A)
38
39
Independência Entre Dois Eventos
Exemplo de Probabilidade Condicional
Modelagem Analítica
É interessante observar que
Modelagem Analítica
Escolha aleatória sem reposição
• Se P(A) e P(B) são estritamente positivos ( > 0 ) e A
e B são eventos mutuamente exclusivos
– Então A e B NÃO SÃO estatísticamente
independentes
Sendo A ∩ B = ∅, tem - se P ( A ∩ B ) = 0 e portanto
P(B | A) = 0 ≠ P(B)
• de uma população de n elementos 1, 2, ..., n, tomantoman-
se uma amostra ordenada.
• considerando que o primeiro elemento é o elemento
i, qual é a probabilidade de que o segundo elemento
seja o elemento j ?
• Logo, se os eventos A e B são independentes e
mutuamente exclusivos
– Então pelo menos um deles tem probabilidade nula
40
41
Exemplo de Probabilidade Condicional
Partição do Espaço de Amostras
Modelagem Analítica
Um conjunto de eventos {B
{Bi}, i = 1, ..., n constitui uma
partição do espaço de amostras Ω quando satisfaz as
duas condições a seguir
1
P( A ∩ B) =
n(n − 1)
1
P( B) =
n
1
P( A | B) =
(n − 1)
Modelagem Analítica
1) Bi ∩ B j = ∅, ∀ i, j = 1, K, n (i ≠ j )
n
Isso expressa o fato de que a segunda
escolha é feita sobre uma população
de n−
−1 elementos, todos com a
mesma probabilidade.
2) U Bi = Ω
De uma forma geral:
Em um experimento de escolhas
sucessivas, independente das
primeiras r escolhas, na escolha de
número r+1, as n−r opções restantes
têm probabilidade 1/(n − r).
• Os eventos que compõem uma partição são
42
i =1
– mutuamente exclusivos e,
– quando unidos, englobam todo o espaço de amostras
43
Partição do Espaço de Amostras
Teorema da Probabilidade Total
Modelagem Analítica
Ω
Considere um evento A e uma partição do espaço
de amostras {B
{Bj}, j = 1, ..., m. Para essa partição e
esse evento temtem-se que
B4
B2
Modelagem Analítica
B3
m
P( A) = ∑ P( A ∩ B j )
B1
j =1
B5
ou ainda
B6
B7
m
P( A) = ∑ P( A | B j ) ⋅ P ( B j )
j =1
44
45
Teorema da Probabilidade Total
Teorema da Probabilidade Total
Modelagem Analítica
Ω
Demonstração
B4
B2
B3
B5
B7
Demonstração
m

A = A ∩ U B j 
 j =1 
Tendo em vista que a interseção é distributiva em relação à
união, tem-se que
B1
A
Modelagem Analítica
B6
m

A = U ( A ∩ B j ) 
 j =1

(1)
Como B j ∩ Bk = ∅ ∀j ≠ k ( j , k = 1,K m ) , pois {Bi } é uma partição,
A = A∩Ω
então
m

A = A ∩ U B j 
 j =1 
( A∩ B )∩( A∩ B ) = ∅
j
46
k
47
Teorema da Probabilidade Total
Regra de Bayes
Modelagem Analítica
Demonstração (cont)
Logo, os termos da união (1) são mutuamente exclusivos e,
portanto
Modelagem Analítica
Considere uma partição {B
{Bj}, j = 1, ..., m do espaço de
amostras, com P(Bj ) > 0 para todo j. Seja ainda A, um
evento com P(A
P(A)) > 0.
Utilizando a definição de probabilidade condicional
P ( B j ∩ A)
P( B j | A) =
(1)
P ( A)
P ( B j ∩ A)
P( A | B j ) =
P( B j )
m
P( A) = ∑ P( A ∩ B j )
j =1
⇒ P ( B j ∩ A) = P( A | B j ) ⋅ P ( B j )
(2)
Pelo teorema da probabilidade total
m
P( A) = ∑ P ( A | Bk ) ⋅ P ( Bk )
(3)
k =1
48
49
Regra de Bayes
Exemplo
Modelagem Analítica
Substituindo (2) e (3) em (1)
P( B j | A) =
P( A | B j ) ⋅ P ( B j )
m
∑ P( A | B
k
) ⋅ P ( Bk )
• Essa expressão é conhecida como Regra de Bayes
• As probabilidades P(Bj ) são conhecidas como probabilidades
a priori
• As probabilidades P(Bj | A) são conhecidas como
50
Suponha uma população de seres humanos dividida em
subpopulações H1, H2, ... disjuntas
•
j = 1, K, m
k =1
probabilidades a posteriori
Modelagem Analítica
divisão segundo algum critério qualquer como faixa etária,
grupo étnico etc.
Seja P(H
P(Hj) a probabilidade de um indivíduo pertencer a
Hj
Seja P(A | Hj ) a probabilidade de um indivíduo
pertencente a Hj ser canhoto.
1. Qual é a probabilidade de um indivíduo qualquer ser
canhoto ?
2. Sabendo que um indivíduo é canhoto, qual é a
probabilidade dele pertencer ao grupo Hj ?
51
Exemplo
Modelagem Analítica
1. P( A) = ∑ P ( A | H j ) P( H j )
(Teorema da probabilidade total)
k
2. P( H j | A) =
P( A | H j ) P( H j )
∑ P( A | H
k
) P( H k )
k
52
(Regra de Bayes)