6º ano em 2016 - Colégio OBJETIVO

Nome: _________________________________________
____________________________ N.º: __________
endereço: ______________________________________________________________ data: __________
Telefone:_________________ E-mail: _________________________________________________________
Colégio
PARA QUEM CURSA O 6.O ANO DO ENSINO FUNDAMENTAL EM 2016
Disciplina:
Prova:
MaTeMÁTiCa
desafio
nota:
QUESTÃO 16
(OBM-adaptado) – No sistema decimal de numeração, um número tem 3 classes e 7 ordens.
Então esse número tem:
a) 10 algarismos.
b) 9 algarismos.
c) 8 algarismos.
d) 7 algarismos.
e) 4 algarismos.
RESOLUÇÃO
Classes
milhões
milhares
unid. simples
Ordens
Resposta: D
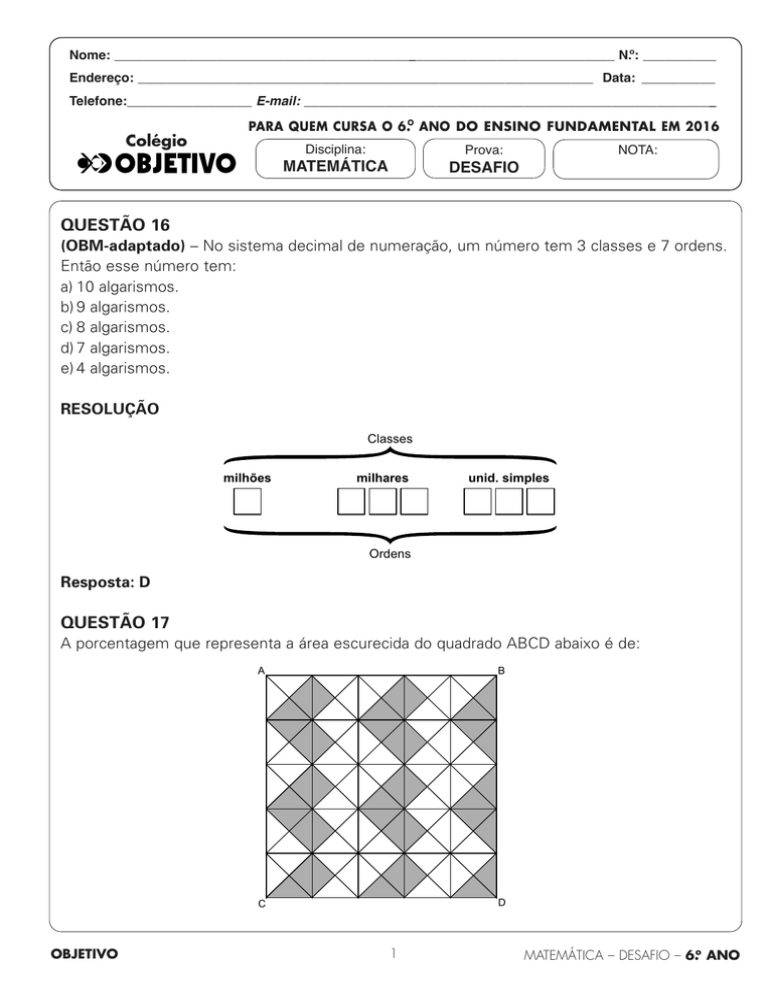
QUESTÃO 17
A porcentagem que representa a área escurecida do quadrado ABCD abaixo é de:
OBJETIVO
A
B
C
D
1
MATEMÁTICA – DESAFIO – 6.o ANO
a) 40%
b) 58%
c) 35%
d) 49%
e) 30%
RESOLUÇÃO
O quadrado ABCD está dividido em 100 triângulos iguais que representam 100% da
figura.
A área escurecida é de 40 triângulos. Assim, a área escurecida representa 40% da figura
Resposta: A
QUESTÃO 18
Observe as frações representadas nas figuras A, B e C, pela parte escurecida em relação ao
todo.
Podemos afirmar que a soma das frações representadas por A, B e C é igual a:
13
a) –––
10
17
b) –––
20
c) 1
19
d) –––
20
9
e) –––
10
OBJETIVO
2
MATEMÁTICA – DESAFIO – 6.o ANO
RESOLUÇÃO
1
1
2
As frações representadas são: A = –– ; B = –– e C = ––
2
4
10
A soma das frações representadas por A, B e C é:
1
1
2
10 + 5 + 4
19
–– + –– + –– = –––––––––– = ––
2
4
10
20
20
Resposta: D
QUESTÃO 19
Observe o que aconteceu na decomposição em fatores primos, a seguir:
A , 350
150 , B
2
C
D , 175
3
E , F
5
5 , G
5
1 , 7
H
1 , 1
Não podemos afirmar que:
a) G é múltiplo de H.
b) E é divisor de D.
c) C é par e primo.
d) 350 – B = F.
e) G é divisor de D.
RESOLUÇÃO
A decomposição apresentada é
OBJETIVO
300 , 350
2
150 , 175
2
75 , 175
3
25 , 175
5
5 , 35
5
1,
7
7
1,
1
3
MATEMÁTICA – DESAFIO – 6.o ANO
Assim,
A = 300
F = 175
B = 175
G = 35
C=2
H=7
D = 75
E = 25
Só não é correto afirmar que G é divisor de D, pois 35 não é divisor de 75.
Resposta: E
QUESTÃO 20
Os números desta questão estão escritos em algarismos romanos.
Se ao décuplo de CCCXLIV for adicionado o óctuplo de CXXIX encontraremos:
a) MMMMCDLXXII
b) MMMXCLXX
––
c) IVCDLXXII
d) IIIDLXXXII
e) MMDCCCII
RESOLUÇÃO
O número romano CCCXLIV é escrito 344 no sistema decimal.
O décuplo de 344 é igual a 10 . 344 = 3440
O número romano CXXIX é escrito 129 no sistema decimal.
O óctuplo de 129 é igual a 8 . 129 = 1032.
Somando-se 3440 e 1032 obteremos 4472 que escrito em números romanos é igual
–––
a IVCDLXXII.
Resposta: C
QUESTÃO 21
(FUVEST-adaptado) – Ao escalar uma trilha de montanha, um alpinista percorre 256m na
primeira hora, 128m na segunda hora, 64m na terceira hora e assim sucessivamente. Para
completar um percurso de 504m, o tempo necessário é de:
a) 5 horas
b) 1960 segundos
c) 6 horas e 30 segundos
d) 380 minutos
e) 21600 segundos
RESOLUÇÃO
Seguindo o raciocínio do problema temos:
1.a hora 256m
2.a hora 128m
3.a hora 64m
4.a hora 32m
OBJETIVO
4
MATEMÁTICA – DESAFIO – 6.o ANO
5.a hora 16m
6.a hora 8m
––––––
504m
Para completar o percurso serão necessários 6 horas = 360min = 21600s
Resposta: E
QUESTÃO 22
(CESGRANRIO) – A figura a seguir mostra três dados iguais. O número da face que é a base
inferior da coluna de dados:
a) é 1.
b) é 2.
c) é 4.
d) é 6.
e) pode ser 1 ou 4.
RESOLUÇÃO
Analisando os números que aparecem nos três dados e lembrando que os três dados
são iguais, podemos concluir que cada dado tem as faces numeradas como mostra a
figura abaixo:
Observe que estes não são dados tradicionais,
pois a soma das faces opostas nem sempre é 7.
O dado da base da pirâmide tem o número 5 na
frente, o 6 no fundo, o 3 do lado direito, o 4 do
lado esquerdo, o 2 em cima e o 1 embaixo,
como mostra a figura abaixo:
Resposta: A
OBJETIVO
5
MATEMÁTICA – DESAFIO – 6.o ANO
QUESTÃO 23
10cm
Uma caixa de papelão planificada apresenta as seguintes medidas:
18cm
18cm
18cm
10cm
10cm
10cm
18cm
A quantidade de papelão usada para fazer a caixa é:
a) 0,1044 m2
b) 10440 mm2
c) 10400 cm2
d) 1,044 m2
e) 104,4 dam2
RESOLUÇÃO
Dividindo a caixa planificada em quadrado e retângulos, temos:
1
10cm
18cm
3
5
2
18cm
4
4 retângulos de 10cm por 18cm, que totalizam, 180cm2 x 4 = 720cm2,
1 quadrado de 18cm por 18cm, ou seja, 324cm2
A área total do papelão usado para fazer a caixa foi de
(720cm2 + 324cm2) = 1044cm2 = 0,1044m2
Resposta: A
OBJETIVO
6
MATEMÁTICA – DESAFIO – 6.o ANO
QUESTÃO 24
O segmento abaixo foi dividido em 10 partes iguais. Nele, estão representados dois números.
Observe:
A
C
B
1,4
1,6
A soma dos números que estão representados pelos pontos A, B e C é igual a:
11
a) ––––
2
9
b) ––––
4
11
c) ––––
4
4
d) ––––
3
9
e) ––––
2
RESOLUÇÃO
Cada intervalo equivale a 0,05.
O ponto A representa o número 1,35
O ponto B representa o número 1,5
O ponto C representa o número 1,65
45
9
1,35 + 1,5 + 1,65 = 4,5 = –––– = –––
10
2
Resposta: E
OBJETIVO
7
MATEMÁTICA – DESAFIO – 6.o ANO
QUESTÃO 25
1
1
1
O resultado de 5 ––– + 1 ––– – 2 ––– equivale a:
4
2
5
11
a) 4 –––
20
11
b) 3 –––
20
1
c) 200% de 2 –––
10
1
d) 200% de 2 –––
20
31
e) 50% de 3 –––
20
RESOLUÇÃO
1
1
1
21
3
11
105 + 30 – 44
91
11
5 ––– + 1 ––– – 2 ––– = ––– + ––– – ––– = ––––––––––––– = –––– = 4 ––––
4
2
5
4
2
5
20
20
20
Resposta: A
QUESTÃO 26
(PUC-RJ) – Um terreno retangular de 108 m x 51 m vai ser cercado como arame farpado
fixado em estacas igualmente espaçadas. Se existe uma estaca em cada vértice, então o
número mínimo de estacas a usar é:
a) 102
b) 104
c) 106
d) 108
e) 110
OBJETIVO
8
MATEMÁTICA – DESAFIO – 6.o ANO
RESOLUÇÃO
2
8
2
Observando que
temos:
108
51
6
6
3
0
3
mdc (108, 51) = 3
Como o perímetro do terreno é 318 m, o número mínimo de estacas é 318 : 3 = 106
Resposta: C
QUESTÃO 27
Para numerar todas as páginas de um trabalho escrito de História, o grupo de Ana utilizou 55
algarismos, iniciando com a página 1. Podemos afirmar que o trabalho tinha:
a) 34 páginas
b) 43 páginas
c) 72 páginas
d) 25 páginas
e) 82 páginas
RESOLUÇÃO
Enumerando as páginas, teremos:
1, 2, 3 .......................................... 9
10, 11, 12, ................................... 19
20, 21, 22, ................................... 29
30, 31, 32
Æ
Æ
Æ
Æ
9 algarismos
20 algarismos
20 algarismos
6 algarismos
––––––––––––––
Total: 55 algarismos
Portanto 32 páginas. Decompondo o número 32, teremos:
32
16
8
4
2
1
2
2
2
2
2
2
25
Resposta: D
OBJETIVO
9
MATEMÁTICA – DESAFIO – 6.o ANO
QUESTÃO 28
O pai de Riquinho abriu várias contas bancárias para seu filho, porém determinou que
Riquinho só poderia retirar mensalmente até R$ 500,00 de cada conta.
Foram abertas cinco contas bancárias e os valores depositados foram:
1)
2)
3)
4)
5)
Banco
Banco
Banco
Banco
Banco
Atende Bem: R$ 500,00
Tupiniquim: R$ 400,00
Nosso Mundo: R$ 1 100,00
do Cliente: R$ 2 100,00
da Praça: R$ 300,00
No 1º mês, Riquinho retirou tudo que era permitido, e isso correspondeu a:
a) metade da quantia total que foi depositada.
b) mais do que a metade da quantia depositada.
c) a terça parte do que foi depositado.
d) tudo que foi depositado.
3
e) –– do que foi depositado.
4
RESOLUÇÃO
O depósito total feito pelo pai de Riquinho foi:
R$ 500,00 + R$ 400,00 + R$ 1 100,00 + R$ 2 100,00 + R$ 300,00 = R$ 4 400,00
A retirada total de Riquinho foi igual a soma de R$ 500,00 (do Banco Atende Bem), mais
R$ 400,00 (do Banco Tupiniquim), mais R$ 500,00 (do Banco Nosso Mundo), mais
R$ 500,00 (do Banco do Cliente) e mais R$ 300,00 (do Banco da Praça).
O total retirado é R$ 2 200,00.
Como R$ 4 400,00 ÷ 2 = R$ 2 200,00, Riquinho retirou, exatamente, a metade do que
seu pai depositou.
Resposta: A
OBJETIVO
10
MATEMÁTICA – DESAFIO – 6.o ANO
QUESTÃO 29
Na pirâmide, observe que o número do tijolinho D é a soma dos tijolinhos H e G. Se o número
de cada tijolo da segunda, terceira e quarta linha (de baixo para cima) é a soma dos números
dos dois tijolos imediatamente abaixo dele, o quociente entre A e B será:
A
C
14
B
F
11
E
3
J
10
D
9
I
1
H
2
G
7
13
a) ––––
6
6
b) ––––
13
13
c) ––––
26
13
d) ––––
7
13
e) ––––
8
RESOLUÇÃO
B = 9 + 3 = 12
A = 12 + 14 = 26
A
26
13
––– = –––– = ––––
B
12
6
A pirâmide completa fica
A
26
C
14
F
11
J
10
B
12
E
3
I
1
D
9
H
2
G
7
Resposta: A
OBJETIVO
11
MATEMÁTICA – DESAFIO – 6.o ANO
QUESTÃO 30
SUDOKU, um quebra-cabeça numérico muito popular no Japão, está virando mania mundial!
O objetivo do jogo consiste no preenchimento de uma grade com 9 x 9 = 81 espaços, com
números de 1 a 9, sendo que não é permitido repetir o mesmo algarismo nas linhas, nas
colunas e nas caixas 3 x 3 = 9 espaços.
Observe uma grade na qual as linhas estão identificadas por letras maiúsculas de A a I, as
colunas por letras minúsculas de a a i e as caixas 3 x 3 delimitadas por traços bem definidos.
a b c
A
d e
9
B
7 4
C
1
D
2
E
1
f
g h
7
1
2
6 5
8 9
4
5 9
8
3
2
F
4 5
1
G
7
4
H
3 2
9
I
6
5
i
6
2
1
2
8 5
7
Uma pessoa, querendo descobrir qual algarismo deve ser colocado no cruzamento da linha H
com a coluna c, fez as seguintes afirmações:
I. Estão descartados os algarismos 2, 3, 5, 8 e 9 pois, pela lógica do jogo, não podem ser
utilizados nesse cruzamento.
II. Entre os algarismos 4 ou 6, apenas um deles poderá servir nesse cruzamento.
III. O número que deverá ser colocado, no ponto de encontro da linha H com a coluna c, é
o número 1.
Está correta a afirmação:
a) I, apenas
b) I e II, apenas
c) I e III, apenas
d) II e III, apenas
e) I, II e III
RESOLUÇÃO
A afirmação I está correta, pois os algarismos 2, 3, 5, 8 e 9 já fazem parte dos números
da linha H e não podem mais ser usados.
OBJETIVO
12
MATEMÁTICA – DESAFIO – 6.o ANO
A afirmação II não está correta, pois o algarismo 4 (juntamente com 5 e 7) já faz parte
dos que estão na coluna c. O algarismo 6 também não pode ser usado nesse
cruzamento, pois já compõe o grupo de algarismos dispostos na caixa 3 x 3 = 9, que
fica na parte inferior (à esquerda), da grade de SUDOKU.
Dessa forma, a única possibilidade remanescente é o algarismo 1.
Estão corretas as afirmações I e III, apenas.
Resposta: C
OBJETIVO
13
MATEMÁTICA – DESAFIO – 6.o ANO