7885309-Aula-8-Analise-de-Fourier

4.2. ANÁLISE DE FOURIER
 Série de Fourier
 Transformada de Fourier para Sinais Contínuos
 Transformada de Fourier para Discretos (DFT)
1
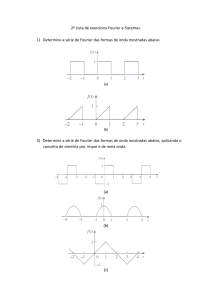
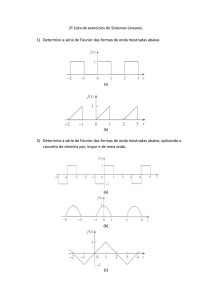
A) Representação de Sinais por Série de Fourier
Introdução
Neste capítulo vamos introduzir as transformações de sinais Série de
Fourier e Transformada de Fourier, que convertem sinais do domínio do
tempo em representações no domínio da freqüência.
Histórico sobre a Série de Fourier
O conceito em usar harmônicos (senos e co-senos) ou exponenciais
complexas para descreverem fenômenos periódicos data de muito tempo
atrás:
1748 – L. Euler – Movimento de uma corda vibratória era combinação dos
modos normais.
1753 – D. Bernoulli – idem
1759 – J. L. Lagrange – Criticou o uso de séries trigonométricas na análise
do movimento de cordas vibratórias. Ele achava que era impossível
representar sinais com descontinuidades usando as séries trigonométricas.
2
1768 – Nasce Jean Baptiste Joseph Fourier em Auxerre, França.
Matemático e Professor na “Ecole Polytechnique de France”.
Vida política intensa. Escapou da guilhotina em duas vezes após a
revolução francesa. Acompanhou Napoleão Bonaparte no Egito.
Prefeito em Grenoble (1802). Nesta cidade desenvolveu suas idéias
sobre série trigonométrica, com aplicação no fenômeno de
propagação de calor e difusão.
1807 – Fourier termina seu trabalho e o apresenta no “Institut de France”.
Foram 4 julgadores de seu trabalho: Lacroix, Monge, Laplace e
Lagrange. Os 3 primeiro a favor da publicação, mas Lagrange foi
veemente contra. O trabalho não foi publicado.
1822 – Publicou o livro “Théorie analytique de la chaleur”, que incluía suas
idéias.
1828 – Dirichlet forneceu condições precisas na qual uma função periódica
poderá ser representada por uma série trigonométrica.
3
Representação em Série de Fourier Trigonométrica de Sinais
Periódicos
Em capítulos anteriores, definiu-se um sinal de tempo contínuo x(t) como
sendo periódico se existir um valor diferente de zero positivo para T tal
que
x(t  T )  x(t )
O período fundamental T0 de x(t) é o menor valor positivo de T para o
qual a equação acima é satisfeita, e 1/T0 = f0 é chamada freqüência
fundamental dada em Hz.
Dois exemplos básicos de sinais periódicos são os sinal senoidal (cosenoidal)
x(t )  cos(0t  )
e o sinal exponencial complexo
x(t )  e j0t
onde 0  2 T0  2f 0 é chamada freqüência angular fundamental.
4
Sendo f(t) uma função periódica com período T. Esta função, caso
obedeça as condições de Dirichlet, pode ser representada pela série
trigonométrica:
f (t ) 
ou
1
a0  a1cos0t  a2cos20t  ...  b1sen0t  b2sen20t  ...
2
a0 
f (t ) 
  (an cos n0t  bnsen n0t )
2 n 1
(1)
A componente senoidal de freqüência n = n0 é chamada o n-ésimo
harmônico da função periódica. O primeiro harmônico é chamado de
componente fundamental, pois ele tem o mesmo período que a
função, e a freqüência correspondente 0 = 2f0 = 2/T é chamada
freqüência angular fundamental (como já mencionado
anteriormente).
5
Convergência da Série de Fourier:
Sabe-se que um sinal periódico f(t) tem uma representação em série de
Fourier se ele satisfazer as seguintes condições de Dirichlet:
(i) A função f(t) é absolutamente integrável em um período, isto é:
T /2
T / 2 | f (t ) | dt  finita

(ii) A função f(t) possui um número finito de máximos e mínimos em um
período.
(iii) A função f(t) possui um número finito de descontinuidades em um
período.
6
A convergência é satisfeita, somente quando um número infinito de
termos for incluído na expansão da série de Fourier. Se a série for
truncada, ou seja, se um número finito de termos for usado na expansão
da série, como na verdade deve ser em quase todas as aplicações práticas,
então a aproximação exibirá um comportamento oscilatório em torno da
descontinuidade, conhecido como Fenômeno de Gibbs. Quando o
número de termos cresce, a curva resultante oscila com freqüência
crescente e a amplitude decrescente.
4 termos na série
16 termos na série
1.5
1.5
1
1
0.5
0.5
0
0
-0.5
-0.5
-1
-1
-1.5
0
0.5
1
1.5
2
Tempo, s
2.5
3
3.5
4
-3
x 10
-1.5
0
0.5
1
1.5
2
Tempo, s
2.5
3
3.5
4
-3
x 10
7
Determinação dos Coeficientes da Série:
Os coeficientes an, a0 e bn são obtidos através da utilização das propriedades
de ortogonalidade das funções trigonométricas.
Um conjunto de funções {k(t)} é ortogonal em um intervalo a<t<b, se para
duas funções quaisquer m(t) e n(t) no conjunto existe a integral
mn
0 ,
T / 2 m (t ) n (t ) dt  rn ,
T /2
mn
Por exemplo, um conjunto de funções senoidais. Pelo calculo elementar,
pode-se mostrar que:
T /2
T / 2
cos m0t dt  0, para m  0
;
T /2
T / 2 sen m0t dt  0, para
todo m
mn
0 ,
cos
(
m

t
)cos
(
n

t
)
dt


0
0
T / 2
T / 2 , m  n  0
T /2
mn
0 ,
sen
(
m

t
)sen
(
n

t
)
dt


0
0
T / 2
T / 2 , m  n  0
T /2
T /2
T / 2 sen (m0t )cos (n0t ) dt  0
8
As equações anteriores mostram que as funções {1, cos0t, cos20t, ...,
cosn0t, ..., sen0t, sen20t, ..., senn0t} formam um conjunto de funções
ortogonais em um intervalo –T/2 < t< T/2.
Usando as equações mostradas em slide anterior e combinando com a
equação (1), chega-se às expressões dos coeficientes da série de Fourier:
2 T /2
an  
f (t ) cos (n0t ) dt , n  0,1,2,...

T
/
2
T
bn 
2 T /2
f (t ) sen (n0t ) dt , n  1,2,...


T
/
2
T
2 T /2
a0  
f (t ) dt

T
/
2
T
(2)
(3)
(4)
Observa-se que (4) está contida em (2). E esta equação (4) mostra que o
primeiro termo da série (a0/2) é o valor médio da função em um período.
Logo, se a função for simétrica em relação ao eixo das abscissas, este
primeiro termo da série é igual a zero.
9
Simetria Ondulatória – Funções Pares e Ímpares
Uma função f(t) é dita par quando satisfaz a condição:
f (-t )  f (t )
As funções pares são simétricas em relação ao eixo dos Y (eixo da
coordenada dependente), portanto:
a
a
 a f (t ) dt  20 f (t ) dt
Uma função f(t) é dita ímpar quando satisfaz a condição:
f (t )   f (t )
As funções ímpares são anti-simétricas em relação a tal eixo, logo:
a
 a f (t ) dt  0
e
f (0)  0
10
Propriedades:
i) Qualquer função f(t) pode ser expressa como a soma de duas
componentes, das quais uma é par e outra é ímpar, ou seja:
f (t )  f p (t )  fi (t )
ii) Se f(t) for uma função periódica par, sua série de Fourier consiste
somente dos termos an (n=0,1,...), ou seja, de uma constante e dos termos
em co-senos:
a0 
f (t ) 
  an cos n0t
2 n 1
iii) Se f(t) for uma função periódica impar, sua série de Fourier consiste
somente dos termos bn (n=1, 2,...), ou seja, de termos em senos:
f (t ) 

 bnsen n0t
n 1
11
Forma Complexa da Séries de Fourier – Espectro de Freqüência
O co-seno e o seno podem ser expressos em função de exponenciais, ou
seja:
1
(5)
cos n0t  (e jnω0t  e  jnω0t )
2
1 jnω0t  jnω0t
(6)
sen n0t 
(e
e
)
2j
As expressões acima são determinadas a partir da equação de Euler:
e  j  cos  j sen
Substituindo (5) e (6) em (1), vem (lembrando que -j=1/j):




a0   1 jn 0t
1 jn 0t
 jn 0t
 jn 0t 
f (t ) 
   an e
e
 bn
e
e

2 n 1 2
2j

a0   1

jn 0t 1
f (t ) 
   (an  jbn )e
 (an  jbn )e  jn 0t 
2 n 1 2
2

12
Definindo:
c0 
1
1
1
a0 , cn  (an  jbn ), c n  (an  jbn )
2
2
2
Logo,

f (t )  c0   (cn e jnω0t  c n e  jnω0t )
n 1

f (t )  c0   cn e
jnω0t
n 1

f (t )  c0   cn e
jnω0t

  c n e  jnω0t
n 1

n 1
f (t ) 

jnω0t
c
e
n
n  1

 cne jnω0t
(7)
Série de Fourier Complexa
n  
13
Determinação dos Coeficientes da Série de Fourier Complexa:
1
cn  (an  jbn )
2
Os coeficientes cn são valores complexos
cn 
T /2
1  T /2

f
(
t
)
cos(
n

t
)
dt

j
f
(
t
)
sen(
n

t
)
dt
0
0
T / 2

T T / 2
1 T /2
cn  
f (t )[cos( n0t )dt  j sen( n0t )]dt

T
/
2
T
1 T /2
cn  
f (t ) e  jn 0t dt
T T / 2
c n 
n  0,1,2,....
1 T /2
jn 0t
f
(
t
)
e
dt


T
/
2
T
Se f(t) for real então:
c n  cn*
O símbolo (*) denota o complexo conjugado
14
cn 
1 T
 jn 0t
f
(
t
)
e
dt

0
T
cn é complexo para todo n com exceção de n=0 (ou seja, c0=(1/2)a0),
então possui módulo e ângulo de fase:
cn | cn | e j n
1
| cn |
(an2  bn2 )
2
e
n  arc tg ( - bn / an )
Um gráfico onde se marcam no eixo horizontal as freqüências dos
harmônicos e no eixo vertical os valores dos coeficientes cn da série
complexa de Fourier, chamamos espectro de amplitudes da função
periódica f(t). No caso de se ter, no eixo vertical, os ângulos de fase n em
função da freqüência, este gráfico chama-se espectro de fases de f(t).
15
Como os índices n assumem somente valores inteiros, os espectros de
amplitudes e de fases, não são curvas contínuas e sim surgem como linhas
verticais (raias) nas variáveis discretas n0. Portanto, tais gráficos denominamse espectro de freqüência discreta. A representação dos coeficientes complexos
cn em função da variável complexa n0 especifica a função periódica f(t) no
domínio da freqüência, do mesmo modo que a função f(t) em função de t a
especifica no domínio do tempo.
É usual representar tais espectros apenas em relação ao eixo de freqüências
positivas, pois o lado esquerdo (lado das freqüências negativas) contém a
mesma informação que o direito, já que os coeficientes c*n são os complexos
conjugados de cn. Na Figura abaixo é mostrado um exemplo de um espectro de
amplitudes.
|cn|
16
Freqüência
B) Transformada De Fourier de Sinais Contínuos
 A expansão por série de Fourier é uma forma de representação de
funções periódicas em termos de um somatório de funções harmônicas.
 Para funções não-periódicas é necessário uma adequação da análise de
Fourier ao problema.
 Nesta análise, um sinal transiente pode ser visualizado como um sinal
periódico tendo seu período tendendo ao infinito.
Da Série de Fourier à Transformada de Fourier:
Seja um sinal não-periódico x(t)=0 para -T1 > t > T1 :
Sinal Transiente
Formando um sinal periódico xp(t) através da repetição de x(t) com
período fundamental T0 :
...
...
Sinal Periódico
17
Relembrando a série complexa de Fourier e a expressão de seus
coeficientes:

1 T0 / 2
- j n 0 t
x p (t )   cn e jn0t
cn 
x
(
t
)
e
dt
p


T
/
2
T0
0
n  
Aqui foi substituído o símbolo da função temporal f(t) por x(t) para evitar
confusão com o símbolo de freqüência f dada em Hz. Substituindo a segunda
na primeira, vem:
 

1 T /2
x p (t )     0
x p (t ) e- jn0t dt  e jn0t
T T0 / 2

n    0
2
T0 
0

 1 T0 / 2

x p (t )    
x p (t ) e- jn 0t dt  0e jnω0t
2 T0 / 2

n   
Quando T0 torna-se muito grande, 0 torna-se muito pequeno. Logo, fazendo
0=, tem-se n0= n, então:
x p (t ) 

 1 T0 / 2
- jn t  jnt
x
(
t
)
e
dt  e

  2 T0 / 2 p

n  
18
No limite, quando T0, n, d, e o somatório torna-se uma
integral:
1   
- jt  jt
x p (t ) 
x
(
t
)
e
dt  e
d
p







2


Assim pode-se definir o termo entre colchetes, na equação acima como:
X ()  


x(t ) e- jt dt
Transformada de Fourier
Logo,
1 
jt
x(t ) 
X
(

)
e
d
2  
Transformada Inversa de
Fourier
As duas integrais acima formam o Par de Integrais de Fourier. Este par
também pode ser escrito por (quando considera-se freqüência em Hz):
X(f )  


x(t ) e
- j 2 ft
dt
x(t )  


X ( f ) e j2πft df
19
Simbologia:
X ( f )  {x(t )}
1
x(t )   { X ( f )}
ou
x(t )    X ( f )
O gráfico de |X(f)| versus f é um espectro contínuo.
No espectro das amplitudes complexas de um sinal periódico, se o período
aumenta, a freqüência fundamental diminui e as componentes em
freqüência dos harmônicos ficam mais próximas entre si, fazendo com que
a disposição das raias tendam a uma distribuição contínua e a série de
Fourier vem a tornar-se uma integral.
CnT0
T
=
4T
Exemplo:
0
1
T0= 8T1
T0= 16T1
20
Convergência das Transformadas de Fourier:
As condições de Dirichlet são condições suficientes, mas não necessárias
para a existência da Transformada de Fourier de uma determinada
função.
Condições de Dirichlet:
(i) A função x(t) é absolutamente integrável em módulo, isto é:

 | x(t ) | dt  finita

(ii) A função x(t) possui um número finito de máximos e mínimos dentro
de qualquer intervalo finito.
(iii) A função x(t) possui um número finito de descontinuidades dentro de
qualquer intervalo finito e cada uma dessas descontinuidades é finita.
Funções periódicas não obedecem à condição (i), mas possuem
transformadas, caso funções impulsos estejam presentes na
transformação. As funções aleatórias não atendem à condição (i).
21
Propriedades das Transformadas de Fourier:
(i) Linearidade
Se x(t)  X() e se y(t)  Y(), então
ax( t )  by( t )    aX (  )  bY( )
(ii) Atraso no tempo
x( t  t 0 )    X (  ) e -jt0
(iii) Atraso na freqüência
x( t )e j0t    X (   0 )
(iv) Escalonamento
x( at )   
1
 
X 
|a| a
22
(v) Reverso no tempo
x( t )    X ( )
(vi) Diferenciação ou Integração
d
x( t )    j 2f X( f ) , ou
dt
d
x( t )    j  X(  ) , ou de modo geral
dt
dn
dt n
x( t )    (j  ) n X(  )
 j t x( t )   
d
X ( )
d
t
1
X (  )   X (0) ()
j

x( t )dt   
23
(vii) Simetria ou Dualidade
X ( t )    2 x(  )
X (t )    x(f )
(viii) Propriedades da T.F quando a função é real
x(t)  X()
x( t )  x par ( t )  x impar ( t )
x(t )  
X (  )  Re(  )  j Im(  )
então
{x(t )}  {x par (t )}  {ximpar (t )}
Re()  {x par (t )}
j Im()  {ximpar (t )}
A T.F. de uma função
par será sempre real
24
x( t )  x par ( t )  x impar ( t )
x(t )  x par (t )  ximpar (t )
x(t )  x par (t )  ximpar (t )
Aplicando a T.F.
{x(t )}  {x par (t )  ximpar (t )}
{x(t )}  {x par (t )}  {ximpar (t )}
X ()  Re ()  j Im()  X  ()
Então, se x(t) for uma função real então:
X ()  X  ()
25
Exemplos de Aplicação da Transformada de Fourier:
i)
T.F. da Função Pulso Retangular Simétrico
x(t )  A, | t | T0
x(t )  0,
X(f )  

x(t ) e -j 2πft dt

X( f )  
T0
T0
X( f ) 
A
Ae

-j 2πft
T0
-j 2πf T0

X( f ) 
e-j 2πfT
-j 2πf
A
0
X( f ) 
| t | T0
dt  A
T0
T0
A
f


u
-j 2πft T0
e
T0
-j 2πf
j 2πfT0
  Af 21j e j 2πfT
A e du 
e
e-j 2πft dt
A
0
 e  j 2πfT0

sen( 2πfT0 )
26
X( f ) 
A
f
sen( 2πfT0 )

2T0
2T0
sen( 2πfT0 )
X ( f )  2 AT0
2fT0
X ( f )  2 AT0 sinc (2πfT0 )
Função Real
27
(ii) T.F. da Função Pulso Retangular (Função Porta)
X (f ) 

0 A e
- j2ft

A
A
A
- j2ft
dt 
e

(e - j2f - 1) 
e - jf (e - jf - e  jf )
- j2f
- j2f
- j2f
0
X( f ) 
sen( f) - jf
A - jf 1 jf
e
[ (e
- e  jf )]  A
e
f
2j
f
X ( f )  A sinc(f)e -jf
| X ( f ) | A | sinc(f) |
X ( f )  arc tg [tg(f)]
28
Funções portas com diferentes durações e magnitudes das
respectivas transformadas
Magnitude da Transformada de Fourier da Função Porta
Função Porta
0.2
1.2
0.18
1
0.16
0.14
0.8
0.12
0.1
0.6
0.08
0.4
0.06
0.04
0.2
0.02
0
0
0.5
1
1.5
2
2.5
Tempo [s]
3
3.5
4
4.5
0
-10
5
-8
-6
-4
-2
0
2
Freqüência [Hz]
4
6
8
10
Função Porta
1.2
Magnitude da Transformada de Fourier da Função Porta
0.1
1
0.09
0.08
0.8
0.07
0.06
0.6
0.05
0.4
0.04
0.03
0.2
0.02
0
0.01
0
0.5
1
1.5
2
2.5
Tempo [s]
3
3.5
4
4.5
5
0
-10
-8
-6
-4
-2
0
2
Freqüência [Hz]
4
6
8
10
Percebe-se que quanto menor a duração da porta, o
primeiro “vale” no espectro da transformada será
mais prolongado
29
(iii) T. F. do Impulso
x(t )  K (t )
X (f )  { x(t )} 

 
Portanto,
Logo,

 
K (t ) e
- j2ft
dt  K
(t  t 0 ) x(t ) dt  x(t 0 )
X (f )  K

 

 
(t ) e - j2ft dt
Propriedade da função
Delta de Dirac
(t ) e - j2ft dt  K e - j2f0  K
{K (t )}  K
Daí o motivo de se usar excitação impulsiva na análise modal experimental,
pois teoricamente o impulso excitaria todas as freqüências do sistema sob teste
30
iv) T.F. de uma Constante
Do caso anterior, tem-se:
K(t )    K
Segundo a propriedade de simetria (X(t) x(-f))
K    K( f )
e levando-se em conta que (f)= (-f):
K    K ( f )
Logo,
{K }  K( f )
{K }  2K()
31
iv) T.F. da Função Co-seno
1 j0t
x(t )  (e
 e  j 0 t )
2
1
1
j0t
X ()  {x(t )}  {e
}  {e  j0t }
2
2
x(t )  cos(0t )
* Obs : {x(t )e j t }  X (  0 )
0
* Obs : {K}  2K()
1
1
X ()  2(  0 )  2(  0 )
2
2
1
1
X ()  (  0 )  (  0 ) X ( f )  ( f  f 0 )  ( f  f 0 )
2
2
A T.F. do co-seno consiste de duas funções delta de Dirac simétricas,
uma localizada em f0 e outra em - f0.
32
Teorema Parseval para Sinais Não-Periódicos de Energia finita
Sendo x(t) um sinal de energia finita, sua energia é dada por:
Ex  


| x(t ) |2 dt
que pode ser expressa em termos de X(f), ou seja:







Ex   x(t ) x (t )dt   x(t ) X  ( f )e j 2ft df  dt


 



Ex   x(t ) x (t )dt   X ( f ) x(t )e j 2ft dt df


 

Ex  



Então,


X ( f ) X ( f ) df  


Ex  


| X ( f ) |2 df
| x(t ) | dt  
2


| X ( f ) |2 df
A energia do sinal pode ser descrita no domínio do tempo ou
no domínio da freqüência.
33
Ex  


| X ( f ) |2 df
 O termo |X(f)|2 representa a distribuição de energia do sinal
em função da freqüência.
| X ( f ) |2  S xx ( f )
 Sxx(f)  Auto Densidade Espectral de Energia do Sinal x(t)
 Será visto posteriormente que a função auto densidade
espectral, Sxx(f), é a transformada de Fourier da função de
auto correlação, Rxx().
{Rxx ()}  S xx ( f )
34
C) TRANSFORMADA DE FOURIER DISCRETA
 A Transformada de Fourier têm sido usada com sucesso através dos anos
para resolver muitos tipos de problemas de engenharia, física e matemática.
Esta transformada, como já visto, é definida para funções contínuas (ou
analógicas).
 A partir dos anos 60 a transformada de Fourier tem sido implementada na
forma digital (surgindo a Transformada de Fourier Discreta) em vários tipos
de analisadores. Estes analisadores computam a forma digital (ou
discretizada) de espectros de potência, funções de resposta em freqüência e
outras funções no domínio da freqüência a partir de sinais medidos
(amostrados) no domínio do tempo, todos a partir da Transformada de
Fourier Discreta.
 Nesta seção é apresentada a técnica conhecida com Transformada de
Fourier Discreta (TFD) ou DFT (sigla da técnica em inglês) para seqüências
de comprimento finito.
35

A implementação da Transformada Discreta de Fourier ou simplesmente
DFT (“Discrete Fourier Transform”), veio a ser prática em 1965 quando
Cooley e Turkey descreveram um algorítmo para computar a DFT de
forma bem eficiente. Seu algorítmo (e outros como ele) tornaram-se
conhecidos como a Transformada Rápida de Fourier ou FFT (“Fast
Fourier Transform”).

Usando o algorítmo da FFT, analisadores digitais de sinais podem
computar a DFT em milisegundos ao invés de horas como era feita em
décadas passadas.

A computação direta da DFT de uma função contendo N pontos, requer
N2 operações; onde uma operação é definida como uma multiplicação
mais uma adição. O algorítmo de Cooley e Tukey requer
aproximadamente Nlog2N operações, sendo N potência de 2.

Muitos outros métodos para computação eficiente da DFT têm sido
descobertos, contudo, todos os quais que requerem em torno de Nlog2N
operações têm sido conhecidos como FFT’s.
36
Seja x[n]uma seqüência de tamanho finito de comprimento N, isto é,
x[ n]  0
Fora do intervalo 0  n  N-1
A TFD (ou DFT) de x[n], representada por X[k], é definida por:
1 N 1
X [k ] 
x[n] WNkn

N n 0
sendo
k = 0,1,.., N-1
WN  e  j ( 2  / N )
A TFD (ou DFT) inversa é dada por:
x[n] 
N 1
 kn
X
[
k
]
W

N
n = 0,1,.., N-1
n 0
Exemplo: Dada a seqüência x[n]=[1, 2, 1]. (a) Calcule a DFT de x[n];
(b) Use o comando da fft no matlab para determinar a DFT de x[n]
37
Solução: (a)
W30  1
W32

 e

 j ( 2 / 3) 2

  0,5  j0,866
3
 j ( 2 / 3) 3
 1
W3  e
W31
 0,5  j 0,866
 e
 j ( 2 / 3) 1
W34  W31
X [0] 
X [1] 
2
0
x
[
n
]
W

3  1 2 1  4
n 0
2
 x[n] W31n  x[0] W30  x[1] W31  x[2] W32 
n 0
 1(1)  2(0,5  j 0,866)  1(0,5  j 0,866)  0,5  j 0,866
X [2] 
2
2n
0
2
4
x
[
n
]
W

x
[
0
]
W

x
[
1
]
W

x
[
2
]
W

3
3
3
3 
n 0
 1(1)  2(0,5  j 0,866)  1(0,5  j 0,866)  0,5  j 0,866
38
(b) Resultados do Matlab:
» x=[1 2 1];
» xfft=fft(x)
xfft =
4.0000
-0.5000 - 0.8660i -0.5000 + 0.8660i
O que se percebe?
R: O Matlab calcula a DFT através da fórmula mostrada com a exceção do
parâmetro (1/N). Portanto o usuário deve dividir o resultado da fft por N.
Por quê?
R: Porque muitos autores definem a DFT sem a divisão por N, que surge
dividindo na expressão da IDFT.
39
Fórmulas da Discretização dos Sinais no Domínio do Tempo e no Domínio
da Freqüência.
T = Tempo (ou Período) de Aquisição ou
Período de Análise ou Registro Temporal
(“Time Record”);
N = Número de Linhas Espectrais
t = Intervalo de Tempo ou de
Amostragem ou Incremento de Tempo;
f = Intervalo de Freqüência ou
Resolução em Freqüência;
fs = Freqüência ou Taxa de amostragem
T  N t
t 
1
fs
 fs 
1
1
f 
 T
T
f
1
t
 Tf  1
Quanto maior a duração da aquisição do sinal,
maior resolução terá o espectro.
40
Princípio da Incerteza
T = Tempo (ou Período) de
Aquisição ou Período de Análise ou
Registro Temporal (“Time Record”);
t = Intervalo de Tempo ou de
Amostragem ou Incremento de
Tempo;
f = Intervalo de Freqüência ou
Resolução em Freqüência;
fs = Freqüência ou Taxa de
amostragem
T  N t
t 
1
fs
 fs 
1
1
f 
 T
T
f
1
t s
 Tf  1
41
Natureza e Disposição dos Coeficientes de Fourier no Espectro
No Matlab (como não pode haver índice zero em variáveis indexadas):
42