P: A velocidade angular da barra AB em θ = 0° caso a barra seja

EXEMPLO 1
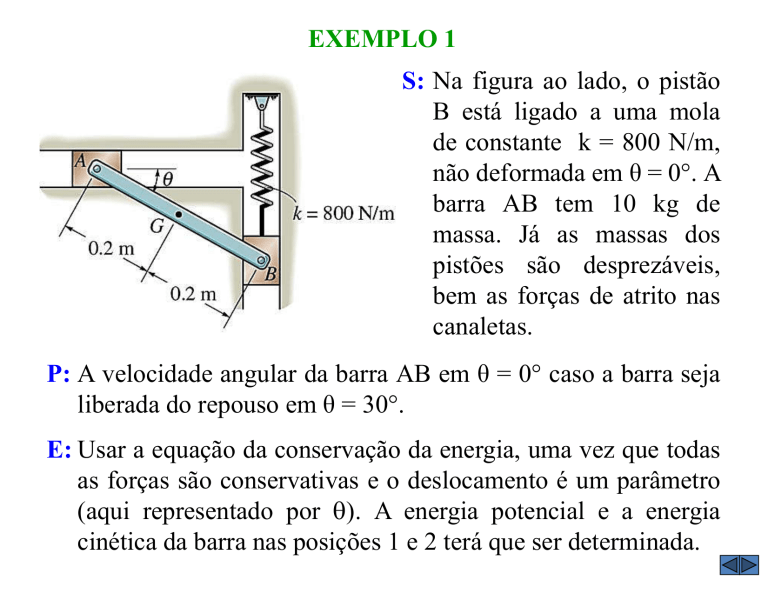
S: Na figura ao lado, o pistão
B está ligado a uma mola
de constante k = 800 N/m,
não deformada em θ = 0°. A
barra AB tem 10 kg de
massa. Já as massas dos
pistões são desprezáveis,
bem as forças de atrito nas
canaletas.
P: A velocidade angular da barra AB em θ = 0° caso a barra seja
liberada do repouso em θ = 30°.
E: Usar a equação da conservação da energia, uma vez que todas
as forças são conservativas e o deslocamento é um parâmetro
(aqui representado por q). A energia potencial e a energia
cinética da barra nas posições 1 e 2 terá que ser determinada.
EXEMPLO 1 (cont.)
Solução:
Posição 1 (inicial)
Posição 2 (final)
Energia Potencial: Colocando a referência alinhada com a barra
quando θ = 0°, tem-se que a energia potencial gravitacional e a
energia potencial elástica serão 0 na posição 2, ou seja, V2 = 0 .
Energia potencial gravitacional em 1: – (10)( 9,81)(0,2 sen30°)
Energia potencial elástica em 1: (½) (800) (0,4 sen30°)2
Assim, V1 = – 9,81 + 16,0 = 6,19 N.m.
EXEMPLO 1 (cont.)
Posição 1 (inicial)
Posição 2 (final)
Energia Cinética: A barra é liberada do repouso na posição 1.
Portanto, T1 = 0.
Na posição 2, a velocidade angular é w2 e a velocidade do centro de
massa vG2 .
Portanto, T2 = (½) (10)(vG2)2 + (½) (1/12)(10)(0,42)(w2)2 .
EXEMPLO 1 (cont.)
Ocorre que, na posição 2, o ponto A é um CI.
Assim, vG2 = rG/CI w2 = 0,2 w2 .
Então,
T2 = 0,2 w22 + 0,067 w22
= 0,267 w22 .
Aplicando agora a equação da conservação da energia e resolvendo
para a incógnita, qual seja, a velocidade angular w2, resulta que
T1 + V1 = T2 + V2
0 + 6,19 = 0,267w22 + 0
w2 = 4,82 rad/s .
EXEMPLO 2
S: O pêndulo de 30 kg tem seu
centro de massa em G, com
raio de giração kG = 0,3 m.
Ele é liberado do repouso,
em θ = 0, sendo que a mola
não se encontra deformada
nessa posição.
P: A velocidade angular do
pêndulo quando θ = 90.
E: Forças conservativas e o deslocamento θ conduzem ao uso da
conservação de energia. Primeiro, determinam-se as energias
potencial e cinética em ambas as posições. Então, aplica-se a
equação de conservação da energia.
EXEMPLO 2 (cont.)
Solução:
Energia Potencial:
Coloca-se a referência em θ = 0.
Lá, ambas as energias potenciais,
gravitacional e elástica, serão 0.
Assim,
Vg1 = Ve1 = 0
Nota-se que o comprimento não
deformado da mola é 0,15 m.
Energia potencial gravitational em θ = 90:
Vg2 = – 30 (9,81) (0,35) = – 103,0 N.m .
Energia potencial elástica em θ = 90:
Ve2 = (½) 300[ 0,62 + 0,452 – 0,15]2 = 54,0 N.m .
EXEMPLO 2 (cont.)
Energia Cinética:
Quando θ = 0°, o pêndulo é
liberado do repouso. Assim,
T1 = 0.
Já em θ = 90°, como o pêndulo
tem movimento de rotação em
torno do ponto O, tem-se que
T2 = (½) IO (w2)2
onde IO = IG + m (dOG)2 = (30) 0,32 + 30 (0,35)2 = 6,375 kg.m2 .
Dessa forma, T2 = (½) 6,375 (w2)2 .
EXEMPLO 2 (cont.)
Substituindo, então, na
equação da conservação
da energia, qual seja,
T1 + V1 = T2 + V2
resulta que
0 + 0 = (½) 6,375 (w2)2 +
(– 103 + 54,0) .
Resolvendo para w2, obtém-se
w2 = 3,92 rad/s .