Excedente do Consumidor

Excedente do Consumidor
Suponha o gráfico 1 abaixo em que a renda inicial é m/p2 e a cesta escolhida é x*. Por
conseguinte a função utilidade, u, e a função utilidade serão, v, assumirão o valor:
ux *  v p1 , p2 , m
A mudança do preço do bem 1 para p1’ gerará uma escolha diferente, representada
por x’ e um nível de utilidade representado por: ux'  v p1 ' , p2 , m.
Pode-se afirmar que: v p1 ' , p2 , m  v p1 , p2 , m representa uma mudança no nível
de bem estar do consumidor. Logo,
a variação da utilidade entre as
Gráfico 1 – Variação
duas curvas apresenta uma
Compensatória
g  p ' , p , v( p , p , m) 
direção. Está claro que outras
p
transformações monótonas da
m
mesma função também
p
representam essas mudanças,
h p ' , p , u 
x'  p ' , p , m 
valorando-as de maneira distinta.
x
Uma transformação monótona


x* p , p ,m
x
especial é a função gasto. Sabe-se
v( p , p , m)
que para preços fixos p
v( p ' , p , m)
1
2
1
2
2
2
1
1
2
2
m
2
*
2
1
2
1
x1 '
x1h
x1*
1
2
2
x1
Uma mudança na utilidade terá
um efeito na função gasto igual a:
g (p , u )
ou seja, uma

u
transformação monótona
No gráfico 1, u(h)=u(x*). No entanto g(p1’,p2,u)‡ g(p1,p2,u)=m, mas
VC  g  p1 ' , p2 , v( p1 ' , p2 , m)  g  p1 ' , p2 , v( p1 , p2 , m) (1)
pode ser entendida como uma variação do nível de utilidade, medido em quantidades
monetárias. Teoricamente, qualquer vetor de preços fixo pode ser utilizado para
realizar a transformação monótona. No entanto, dois vetores são particularmente
interessantes.
A variação compensatória é aquela necessária para levar o consumidor ao nível de
utilidade original, ou seja a variação da renda que compensa o consumidor pela
variação do preço. Ela está representada no gráfico 1 e equivale àquela calculada na
equação 1, ou seja, o quanto tem que se dar (retirar) de renda ao consumidor para que
ele permaneça no mesmo nível de utilidade inicial.
A variação equivalente procura medir o quanto se devia ter dado (retirado) do
consumidor para que ele se encontrasse antes da mudança de preços tão bem
quanto ficou após a mudança de preços. A variação equivalente será representada
por (ver gráfico 2):
VE  g  p1 , p2 , v( p1 , p2 , m)  g  p1 , p2 , v( p1 ' , p2 , m) (2)
Gráfico 2 – Variação Equivalente
m
p2
VE
g  p1 , p2 , v( p1 ' , p2 , m) 
p2
x'  p1 ' , p2 , m
x *  p1 , p2 , m
h( p1 , p2 , v( p1 ' , p2 , m)
v( p1 , p2 , m)
v( p1 ' , p2 , m)
Deve-se informar que a variação compensatória será igual a
VC  g  p1 ' , p2 , v( p1 ' , p2 , m)   g  p1 ' , p2 , v( p1 , p2 , m) 
 m  g  p1 ' , p2 , v( p1 , p2 , m) 
 g  p1 , p2 , v( p1 , p2 , m)   g  p1 ' , p2 , v( p1 , p2 , m)  (3)
No entanto, sabe-se que:
g  p1 , p2 , v( p1 , p2 , m) 
 h1  p1 , p2 , v( p1 , p2 , m)   x1 *
p1
g  p1 ' , p2 , v( p1 , p2 , m) 
 h1  p1 ' , p2 , v( p1 , p2 , m)   x1h
p1
Gráfico 1 e
gráfico 3
A integral da função demanda
hicksiana entre p1’ e p1 é a
variação compensatória.
Gráfico 3 – Demanda hicksiana
para variação compensatória
VC   h1  p1 , p2 , v( p1 , p2 , m)  (4)
p1
p1 '
p1 '
p1
Demanda hicksiana
O mesmo ocorre com a variação
equivalente
VE   h1  p1 , p2 , v( p1 ' , p2 , m)  (5)
p1
p1 '
x1h
x1 *
Gráfico 4 – Curvas de demanda hicksiana e
marshalliana e variação compensatória
Demanda
hicksiana
p1 '
p1
x'  p1 ' , p2 , m
Área pintada é a variação
compensatória
h p1 ' , p2 , u 
h' ( p1 , p2 , v( p1 ' , p2 , m)
x *  p1 , p2 , m
Demanda
marshalliana
Demanda
hicksiana
x1
A dimensão da variação do excedente varia, portanto, de acordo com o vetor
de preços escolhido. Existem, no entanto, preferências que têm uma
características especial: seu excedente não varia em função do vetor de preços
escolhido. Essas preferências são as quase-lineares.
Gráfico 5 – Curvas de demanda hicksiana e
marshalliana e variação equivalente
Demanda
hicksiana
p1 '
p1
x'  p1 ' , p2 , m
Área pintada é a variação
equivalente
h p1 ' , p2 , u 
h' ( p1 , p2 , v( p1 ' , p2 , m)
x *  p1 , p2 , m
Demanda
marshalliana
Demanda
hicksiana
x1
Repare que a mensuração da variação da satisfação do consumidor difere de acordo
com o critério utilizado, ou seja, se é a variação equivalente ou a variação
compensatória. Deve-se pensar, no entanto, que a variação de quantidade observada e
que, de fato, ocorre é aquela apresentada pela demanda marshalliana. Nesse caso,
entretanto, não se pode pensar em uma medida monetária pois os dois vetores preços
são diferentes, retirando da função gasto a característica de transformação monótona.
Preferências Quase-lineares
As preferências quase-lineares podem ser denotadas por:
u( x1 , x2 )  v( x1 )  x2
A resolução do problema de maximização da utilidade com restrição orçamentária conduz a:
L  v x1   x2   m  p1 x1  p2 x2 
L
 v'  x1   p1  0 com igualdade para x1  0 (6)
x1
L
 1  p2  0 com igualdade para x1  0 (7)
x2
l
 m  p1 x1  p2 x2   0 com igualdade por monotonicidade

A partir de (6) e (8) e normalizan do - se p2  1
(8)
v'  x1   p1 com igualdade se x1  0 (9)
Note - se que o bem 2 é o numerário, ou seja, sua utilidade marginal é 
Isto conduz o bem 1 a não sofrer modificações pelo efeito renda.
x2
Gráfico 6 – Preferências Quase-Lineares:
efeito substituição e efeito renda
gh=p’.xh (p1’,1, v*(p1,1,m)
VC
VE
gE=p.xE (p1,1, v’(p1’,1,m))
xh
x'
x*
xE
v*(p1,1,m)
v’(p1,1,m)  p1
 p1 '
x1h  x1 ' x1E  x1 *
x1
O gráfico 6 apresenta preferências quase-linerares. O consumidor escolheu x*(p1,1,m), ou seja, quando
resolveu o problema de maximização da utilidade aos preços p1 e 1 e renda m. Com a mudança do preço
do bem 1 para p1’, o consumidor escolheu a cesta x’(p1’,1,m). Para calcular a variação compensatória,
deve-se resolver o problema de minimização do gasto quando o preço do bem 1 é p1’ e o nível de
utilidade é v*(p1,1,m), em que v é a função indireta de utilidade, ou seja, obtém-se xh (p1’,1, v*(p1,1,m)).
Adicione-se que também se resolve o problema de minimização do gasto quando os preços são p1 e 1 e
o nível de utilidade, v*(p1’,1,m), para calcular a variação equivalente, obtendo-se xE (p1,1, v’(p1’,1,m)).
A multiplicação do vetor de preços p’=(p1’,1) pelo vetor de quantidades xh (p1’,1,
v*(p1,1,m)) conduz ao gasto gh=p’.xh (p1’,1, v*(p1,1,m) e a diferença entre m e este
gasto é a variação compensatória, ou seja, o quanto o consumidor perdeu com a
elevação do preço do bem 1 e, portanto, o quanto deve-se dar ao consumidor para
compensar essa perda. Da mesma maneira, a multiplicação do vetor p=(p1,1) por xE
(p1,1, v’(p1’,1,m)) leva a gE=p.xE (p1,1, v’(p1’,1,m)) que subtraindo-se m conduz à
variação equivalente, ou seja, o ganho equivalente necessária ao consumidor para
estar aos preços iniciais com a renda m. No entanto, por ser a função utilidade
quase-linear, as duas variações são exatamente iguais, conduzindo a curvas de
demanda hicksiana para o bem 1 exatamente iguais que coincidem com a curva de
demanda marshalliana, como aparece no gráfico 7. Esta é a especificidade das
preferências quase-linerares.
Gráfico 7 – Curva de demanda hicksiana e
marshalliana para preferências quase-lineares
p1 '
p1
x1h  x1 '
x1E  x1 *
x1
p1
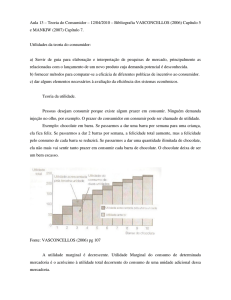
Pense, então, em preferências quase-lineares, mas em bens discretos, ou seja, cuja a
quantidade não varia continuamente. Sabe-se que, em equilíbrio, a utilidade marginal se
igualará ao valor do preço do bem 1, ou mais precisamente à razão entre o preço do bem
1 e o preço do bem 2, sendo o preço do bem 2 igual a 1. Pela equação (9), se o preço do
bem 1 se igualar à Umg(1)=r1, o consumidor só consumirá uma unidade do bem 1. Se for
superior, o consumidor nada consumirá. Na medida em que o preço desça, o consumidor
escolherá consumir mais unidades do bem 1. O ponto é que r1 é o valor máximo que o
consumidor aceita pagar por uma unidade do bem 1, o que denominaremos de preço de
reserva, ou o desejo marginal do consumidor a pagar por uma unidade do bem 1.
Gráfico 8 – Preço de
reserva
r1
r2
r3
1 2 3
Como o bem 2 é o numerário, o preço de reserva
expressa, em termos monetários, o desejo de
consumo do consumidor. Pense, portanto, que o
preço de mercado seja r3. Então, o consumidor
poderá consumir três unidades do bem 1, pela
condição (9). No entanto, deve-se observar que
os preços de reserva da primeira unidade e da
segunda unidade são superiores ao preço pago, o
que significa que o consumidor pagou menos por
essas unidades do que estaria disposto a pagar.
Denominamos a diferença entre o preço de
reserva e o preço pago de excedente do
consumidor.
Em termos um pouco mais formais, podemos estabelecer que o benefício total do
consumidor ou o excedente bruto do consumidor pelo consumo de uma unidade
do bem 1 é representado por sua utilidade total.
v(1). No caso da primeira unidade, a utilidade total é igual à utilidade marginal v' (1) :
r1  v(1)  v(0)
Para a segunda unidade, o excedente bruto do consumidor é representado por:
v(2)  r1  r2
e a utilidade marginal é :
r2  v(2)  v(1)
No entanto, para consumir essas unidades, o consumidor tem de pagar o preço do
bem, p. Ora, no gráfico 8, informamos que o preço de mercado p=r3. Portanto, pela
condição (9), o consumidor consumirá 3 unidades do bem. Pagará por isso 3r3 e
obterá um excedente bruto igual ao somatório de EB=r1+ r2+r3 . Obterá, então um
excedente líquido do consumidor, ou, simplesmente, excedente do consumidor de
EC= r1+ r2+r3 - 3r3. De maneira mais formal:
x
x
EB  v( x)   v' (t )dt   p(t )dt (10)
0
0
x
EC  EB  p.x   p(t )dt  p.x (11)
0
A
x'
EC ( p1 ' )  Ap1 ' B   p(t )dt  p.x'
0
EC ( p1 )  Ap1D   p(t )dt  p.x
C
p1 '
x
0
D
p1
x1h  x1 '
x1E  x1 *
x1
x'
 x'
 x
VC  VE   p(t )dt  p.x    p(t )dt  p.x    p(t )dt   p(t )dt
0
0
0
 0
x
p
p'
p
0
0
p'
  v' ( x)dt   v' ( x)dt   v' ( x)dt  p' pCD
As variações equivalente e compensatória são medidas de variação do excedente
do consumidor, na medida em que capta justamente a variação do excedente
líquido quando o preço varia. Percebe-se, no entanto, que elas só coincidirão em
situações em que não há efeito renda, que são justamente aquelas expressas por
preferências quase-lineares.
O caso de preferências quase-linerares coincide com o que denominamos de
equilíbrio parcial, ou seja, as condições em que o mercado 1 representa uma
parcela tão pequena da renda que variações dos preços implicam uma variação
do gasto total naquele bem que é imperceptível sob o ponto de vista da renda
total, de tal maneira que podemos considerar inexistência de efeito renda. A
teoria marshalliana se desenvolveu nesse âmbito.