INE6006 – Métodos Estatísticos – Exercícios Prova 1- Semestre 2013.1
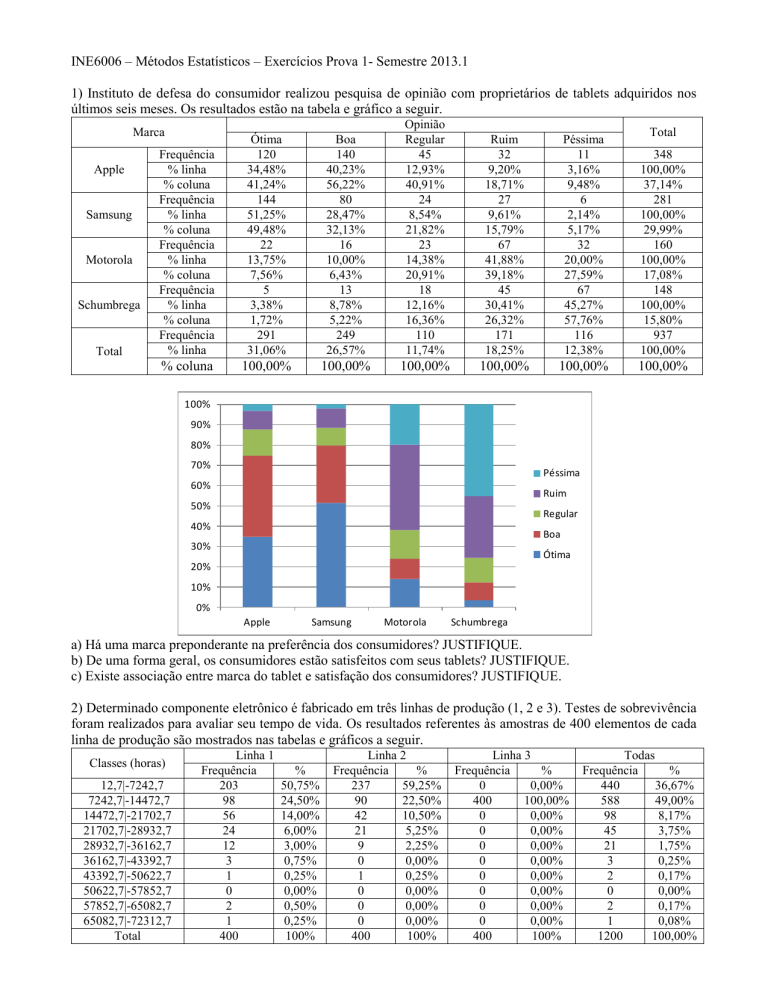
1) Instituto de defesa do consumidor realizou pesquisa de opinião com proprietários de tablets adquiridos nos
últimos seis meses. Os resultados estão na tabela e gráfico a seguir.
Frequência
% linha
% coluna
Frequência
% linha
% coluna
Frequência
% linha
% coluna
Frequência
% linha
% coluna
Frequência
% linha
Ótima
120
34,48%
41,24%
144
51,25%
49,48%
22
13,75%
7,56%
5
3,38%
1,72%
291
31,06%
Boa
140
40,23%
56,22%
80
28,47%
32,13%
16
10,00%
6,43%
13
8,78%
5,22%
249
26,57%
Opinião
Regular
45
12,93%
40,91%
24
8,54%
21,82%
23
14,38%
20,91%
18
12,16%
16,36%
110
11,74%
Ruim
32
9,20%
18,71%
27
9,61%
15,79%
67
41,88%
39,18%
45
30,41%
26,32%
171
18,25%
Péssima
11
3,16%
9,48%
6
2,14%
5,17%
32
20,00%
27,59%
67
45,27%
57,76%
116
12,38%
348
100,00%
37,14%
281
100,00%
29,99%
160
100,00%
17,08%
148
100,00%
15,80%
937
100,00%
% coluna
100,00%
100,00%
100,00%
100,00%
100,00%
100,00%
Marca
Apple
Samsung
Motorola
Schumbrega
Total
Total
100%
90%
80%
70%
Péssima
60%
Ruim
50%
Regular
40%
Boa
30%
Ótima
20%
10%
0%
Apple
Samsung
Motorola
Schumbrega
a) Há uma marca preponderante na preferência dos consumidores? JUSTIFIQUE.
b) De uma forma geral, os consumidores estão satisfeitos com seus tablets? JUSTIFIQUE.
c) Existe associação entre marca do tablet e satisfação dos consumidores? JUSTIFIQUE.
2) Determinado componente eletrônico é fabricado em três linhas de produção (1, 2 e 3). Testes de sobrevivência
foram realizados para avaliar seu tempo de vida. Os resultados referentes às amostras de 400 elementos de cada
linha de produção são mostrados nas tabelas e gráficos a seguir.
Classes (horas)
12,7|-7242,7
7242,7|-14472,7
14472,7|-21702,7
21702,7|-28932,7
28932,7|-36162,7
36162,7|-43392,7
43392,7|-50622,7
50622,7|-57852,7
57852,7|-65082,7
65082,7|-72312,7
Total
Linha 1
Frequência
203
98
56
24
12
3
1
0
2
1
400
%
50,75%
24,50%
14,00%
6,00%
3,00%
0,75%
0,25%
0,00%
0,50%
0,25%
100%
Linha 2
Frequência
%
237
59,25%
90
22,50%
42
10,50%
21
5,25%
9
2,25%
0
0,00%
1
0,25%
0
0,00%
0
0,00%
0
0,00%
400
100%
Linha 3
Frequência
%
0
0,00%
400
100,00%
0
0,00%
0
0,00%
0
0,00%
0
0,00%
0
0,00%
0
0,00%
0
0,00%
0
0,00%
400
100%
Todas
Frequência
%
440
36,67%
588
49,00%
98
8,17%
45
3,75%
21
1,75%
3
0,25%
2
0,17%
0
0,00%
2
0,17%
1
0,08%
1200
100,00%
Medidas
Média (horas)
Mediana (horas)
Qi (horas)
Qs (horas)
D.padrão (horas)
CV%
Qs-Md (horas)
Md-Qi (horas)
Qs-Qi (horas)
Qs+1,5 × (Qs-Qi) (horas)
Qi-1,5 × (Qs-Qi) (horas)
Mínimo (horas)
Máximo (horas)
Assimetria
Curtose
Linha 1
9913,4
7071,5
2679,3
14184
9890,04
99,76%
7112,6
4392,2
11504,7
31441,05
-14577,75
18,0
72307,8
2,11
7,17
Linha 2
8118,9
5554,5
1901,35
11678,4
7902,30
97,33%
6123,9
3653,2
9777,05
26343,975
-12764,225
12,7
49501,4
1,47
2,38
Linha 3
9997,7
10034,5
9376,825
10600,475
876,59
8,77%
566,0
657,7
1223,65
12435,95
7541,35
7647,1
12766,8
-0,03
-0,22
Gráfico de probabilidade do tempo de vida linha 1
Gráfico de probabilidade do tempo de vida linha 2
Exponencial
99,99
95
95
80
80
50
50
Percentual
Percentual
Exponencial
99,99
20
5
20
5
2
2
1
1
10
100
1000
10000
Tempo de vida (horas)
100000
10
Gráfico de probabilidade do tempo de vida linha 3
100
1000
Tempo de vida (horas)
10000
100000
Gráfico de probabilidade do tempo de vida - Total
Exponencial
Exponencial
99,99
99,99
95
95
80
80
50
50
20
Percentual
Percentual
Total
9343,3
9270,3
4332,15
10981,325
7371,41
78,89%
1711,1
4938,1
6649,175
20955,0875
-5641,6125
12,7
72307,8
2,24
10,43
20
5
5
2
1
2
1
10
100
1000
10000
Tempo de vida (horas)
100000
0,01
1
10
100
1000
Tempo de vida (horas)
10000
100000
a) Com base apenas na tabela agrupada em classes há diferenças entre os valores dos tempos de vida de uma
linha de produção para outra? JUSTIFIQUE.
b) Com base apenas nas medidas de síntese do TOTAL de componentes, caracterize a tendência central,
dispersão, assimetria, curtose e existência de discrepantes do tempo de vida.
c) Com base apenas nas medidas de síntese há evidência de diferença nos tempos de vida dos componentes em
função das linhas de produção? JUSTIFIQUE.
d) Com base apenas nas medidas de síntese há evidência de que os tempos de vida dos componentes das três
linhas sigam a distribuição normal? JUSTIFIQUE.
e) Em estudos de confiabilidade geralmente supõe-se que os tempos de vida sigam a distribuição exponencial.
Observando os gráficos de probabilidade dos tempos de vida (das linhas e do total), pode-se concluir que a
suposição é satisfeita? JUSTIFIQUE.
3) Uma rede local de computadores é composta por um servidor e cinco clientes (A, B, C, D e E). Registros
anteriores indicam que dos pedidos de um determinado tipo de processamento, realizados através de uma
consulta, cerca de 10% vêm do cliente A, 15% do B, outros 15% do C, 40% do D e 20% do cliente E. Se o
pedido não for feito de forma adequada, a consulta for feita de forma incorreta, o processamento apresentará
erro. Usualmente os seguintes percentuais de consultas incorretas ocorrem: 1% do cliente A, 2% do cliente B,
0,5% do cliente C, 2% do cliente D e 8% do cliente E.
a) Ao avaliar um determinado processamento deseja-se avaliar como será o resultado do processamento.
Construa o modelo probabilístico para esta situação.
b) Qual é a probabilidade de que o processo tenha sido pedido pelo cliente E, sabendo-se que apresentou erro?
4) Em um sistema de transmissão de dados existe uma probabilidade igual a 0,05 de um dado ser transmitido
erroneamente. Ao se realizar um teste para analisar a confiabilidade do sistema foram transmitidos 20 dados.
a) Calcule a probabilidade de haver erro na transmissão.
b) Qual é o número esperado de erros no teste realizado?
c) Se forem transmitidos 2000 dados, calcule a probabilidade de haver mais de 110 erros.
5) O número de consultas a um banco de dados segue uma distribuição de Poisson com uma taxa de 0,5
consultas por minuto.
a) Para um período de 5 minutos, calcule a probabilidade de que mais de 2 consultas seja feitas.
b) Calcule a probabilidade de que o tempo até a próxima consulta seja de mais de 5 minutos.
6) Certo tipo de cimento tem resistência à compressão com média de 5800 kg/cm2, e desvio padrão de 180
kg/cm2, segundo uma distribuição normal. Dada uma amostra desse cimento, calcule as seguintes
probabilidades:
a) Resistência inferior a 5600 kg/cm2;
b) Resistência entre 5600 kg/cm2 e 5950 kg/cm2;
c) Resistência superior a 6000 kg/cm2, sabendo-se que ele já resistiu a 5600 kg/cm2;
d) se quer a garantia de que haja 95% de probabilidade de o cimento resistir à determinada pressão, qual deve ser
o valor máximo dessa pressão?
INE6006 – Métodos Estatísticos – Exercícios Prova 2- Semestre 2013.1
A resistência interna à pressão (medida em psi) em garrafas de vidro usadas para bebidas gaseificadas é um
aspecto importante de qualidade. Certa fábrica de garrafas tem 3 linhas de produção: A, B e C. Periodicamente,
amostras de 25 garrafas de cada linha são retiradas por sorteio, e encaminhadas ao fabricante de bebidas para
análise. Na última vez que este procedimento foi feito, os resultados abaixo foram encontrados:
Medidas
Linha A
Linha B
Linha C
Total
Média
178,9664
184,142
176,6884
179,9323
Mediana
180,72
184
177,3
179,81
Desvio padrão
8,2279
10,0553
8,5903
9,4095
CV%
4,60%
5,46%
4,86%
5,23%
Qi
174,07
176,17
169,94
174,655
Qs
184,25
189,85
183,13
186,53
Mínimo
159,13
161,24
161,97
159,13
Máximo
193,64
207,13
192,07
207,13
Assimetria
-0,2809
0,1300
-0,0750
0,1351
Curtose
0,2262
0,4853
-0,8526
0,2079
1) O fabricante de bebidas deseja estimar a média de resistência das garrafas provenientes das linhas de
produção A, B e C. Exige confiança de 99%. Sabe-se que as amostras foram retiradas de lotes de 250 garrafas.
Com base nas medidas de síntese da questão 1, obtenha os intervalos de confiança para as médias de resistência
e interprete os resultados.
R.: (A – 174,5913 a 183,3415 psi); (B – 178,7951 a 189,4889);(C – 172,1205 a 181,2563).
2) O fabricante de bebidas necessita que as garrafas apresentem uma resistência média à pressão de no mínimo
175 psi.
a) Aplicando um teste estatístico apropriado, usando 1% de significância e as medidas disponíveis, responda se
as 3 linhas de produção atendem ao requisito. R.: A e C não atendem, B atende.
b) Se a média real fosse de 177 psi, qual seria a probabilidade do teste da letra a detectar isso, supondo que os
desvios padrões amostrais sejam boas estimativas dos desvios padrões populacionais? R.: A = 0,119357656; B =
0,082770116; C =0,109986538 (usando a distribuição t não central).
c) Se desejássemos que o teste da letra a detectasse que a média real vale 177 psi com 90% de probabilidade,
para 1% de significância, supondo que os desvios padrões amostrais sejam boas estimativas dos desvios padrões
populacionais, qual seria o tamanho mínimo de amostra necessário para cada linha de produção? R.: A =
245,6763516; B = 366,9242072; C =267,7992822.
4) Imagine que as garrafas são avaliadas qualitativamente como defeituosas ou não defeituosas. Uma amostra
aleatória de 250 garrafas foi retirada de um lote de 4000. Foram encontradas 41 defeituosas na amostra.
a) Obtenha o intervalo de 95% de confiança para a proporção populacional de garrafas defeituosas. R.:
0,119552936 a 0,208447064.
b) Para uma confiança de 95% e precisão de 3% encontre o tamanho mínimo necessário de amostra, usando a
proporção amostral encontrada e através da estimativa exagerada. R.: 511 e 843.
c) O lote de garrafas somente será aceito se a proporção de defeituosas for inferior a 20%. Com 5% de
significância, usando os resultados da amostra encontrada, o lote será aceito? R. Lote não será aceito.
d) Se a proporção real de defeituosas fosse igual a 18%, e quiséssemos que o teste detectasse isso com 90% de
probabilidade, para a mesma significância de 5%, qual seria o tamanho mínimo de amostra necessário? R: 1811.
5) Aplicando um teste estatístico apropriado, usando 1% de significância e as medidas disponíveis, há evidência
de diferença entre as médias de resistência das garrafas das linhas B e C? E entre A e C? R.: há diferença entre
B e C, não há entre A e C.










