INE 6006 – Exercícios resolvidos

INE 6006 – Exercícios resolvidos - Resolução em itálico, observações em azul.
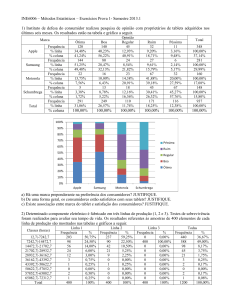
1) A resistência interna à pressão (medida em psi) em garrafas de vidro usadas para bebidas
gaseificadas é um aspecto importante de qualidade. Certa fábrica de garrafas tem 3 linhas de produção:
A, B e C. Periodicamente, amostras de 25 garrafas de cada linha são retiradas por sorteio, e
encaminhadas ao fabricante de bebidas para análise. Na última vez que este procedimento foi feito, os
resultados abaixo foram encontrados:
Medidas
Média
Mediana
Desvio padrão
CV%
Qi
Qs
Qs – Md
Md – Qi
Qi – 1,5×(Qs-Qi)
Qs + 1,5×(Qs-Qi)
Mínimo
Máximo
Assimetria
Curtose
Linha A
Linha B
Linha C
Total
178,9664
184,142
176,6884
179,9323
180,72
184
177,3
179,81
8,2279
10,0553
8,5903
9,4095
4,60%
5,46%
4,86%
5,23%
174,07
176,17
169,94
174,655
184,25
189,85
183,13
186,53
3,53
5,85
5,83
6,72
6,65
7,83
7,36
5,155
158,8
155,65
150,155
156,8425
199,52
210,37
202,915
204,3425
159,13
161,24
161,97
159,13
193,64
207,13
192,07
207,13
-0,2809
0,1300
-0,0750
0,1351
0,2262
0,4853
-0,8526
0,2079
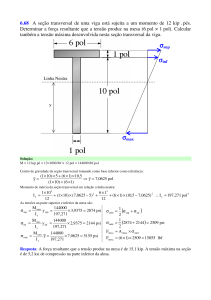
a) Com base apenas nas medidas de síntese do TOTAL de garrafas da tabela acima, caracterize a
tendência central, dispersão, assimetria, curtose e existência de discrepantes da resistência à pressão.
b) Com base apenas nas medidas de síntese é possível considerar que a resistência apresenta
distribuição normal nas 3 linhas de produção?
c) Com base apenas nas medidas de síntese há evidência de diferença na resistência em função das
linhas de produção?
RESOLUÇÃO
a)
Tendência central
O valor típico de pressão oscila entre 179,81 (mediana – 50% dos clientes abaixo e 50% acima deste
valor) e 179,9323 psi (média).
Dispersão
A variação total da pressão é de 159,13 (mínimo) a 207,13 psi (máximo), com um desvio padrão de
9,4095 psi, que representa 5,23% (CV%) da média (não há como saber se é uma dispersão grande ou
não, pois não há padrão de comparação).
Assimetria
A assimetria vale 0,1351 (se igual a zero significa simetria), média e mediana são próximas (179,9323
e 179,81 psi), e a diferença entre quartil superior e mediana (6,72 psi) é semelhante à entre mediana e
quartil inferior (5,155 psi). Tudo isso aponta para uma distribuição simétrica.
Curtose
A distribuição deve ser mesocúrtica, pois o valor de curtose (0,2079) está próximo de zero. Se fosse
leptocúrtica o valor seria consideravelmente maior do que 0, e se platicúrtica, menor.
Existência de discrepantes
Valores menores do que 156,8425 psi seriam discrepantes inferiores. Como o valor mínimo é 159,13
psi, não há discrepantes inferiores. Valores maiores do que 204,3425 psi seriam discrepantes
superiores. Como o valor máximo é 207,13 psi, portanto maior do que 204,3425 psi, pode-se afirmar
que há no mínimo um valor discrepante superior de pressão (o próprio valor de máximo).
b)
Sim, pois das condições necessárias para uma distribuição de uma variável quantitativa poder ser
considerada normal duas são satisfeitas por todas as 3 linhas de produção: a medida de assimetria
precisa ser próxima de zero E a medida de curtose também. Isso ocorre nas três linhas: na linha A,
assimetria -0,2809 e curtose 0,2262; na linha B, assimetria 0,1300 e curtose 0,4853; na linha C,
assimetria -0,0750 e curtose -0,8526. Claro que, em uma situação real usaríamos outros meios para
confirmar isso: gráfico de probabilidade normal, um teste de aderência, etc.
c)
Como as médias e medianas são semelhantes nas três linhas de produção podemos realizar a análise
comparando medianas e quartis.
Os quartis e mediana da linha B são os maiores das três linhas (176,17, 189,95 e 184 psi,
respectivamente), enquanto os da linha C são os menores (169,94, 183,13 e 177,3 psi), e os da linha A
estão em um patamar intermediário (174,07, 184,25 e 180,72 psi). Este mesmo comportamento ocorre
nas médias (184,142 psi na B, 176,6884 psi na C e 178,9664 psi na A). Conclui-se então que há
evidência de diferenças entre as resistências, embora não seja muito grande, pois a maior não passa
de 7 psi (entre as medianas das linha B e C) e a menor de 2 psi (entre as medianas das linhas A e C) .
Novamente, em uma situação real precisaríamos de gráficos, e possivelmente realizar testes de
hipóteses (para comparar as médias das resistências das linhas 2 a 2, ou uma análise de variância,
para avaliar ser há diferenças significativas entre as médias das três linhas. Pelos valores envolvidos,
os testes poderiam indicar que não há diferença significativa entre A e C, mas que talvez haja entre B e
C, veja a questão 5.
2) O fabricante de bebidas da questão 1 deseja estimar a média de resistência das garrafas provenientes
das linhas de produção A, B e C. Exige confiança de 99%. Sabe-se que as amostras foram retiradas de
lotes de 250 garrafas, e informação recente parece indicar que as distribuições das pressões nas 3 linhas
podem ser consideradas aproximadamente normais. Com base nas medidas de síntese da questão 1,
obtenha os intervalos de confiança para as médias de resistência e interprete os resultados.
RESOLUÇÃO
Como as distribuições das resistências nas 3 linhas de produção podem ser consideradas
aproximadamente normais, e as amostras apresentam apenas 25 elementos (menos de 30), e as
variâncias populacionais das resistências são desconhecidas (não há nenhuma informação a respeito),
devemos calcular os intervalos de confiança usando a distribuição t de Student:
s
IC(;99%)  x  t 
n
Como as três amostras têm 25 elementos, e o intervalo tem que ter 99% de confiança, podemos
encontrar o valor de t, tn-1,crítico, para a expressão acima, e usá-lo para determinar os três intervalos:
Procurando na tabela t de Student, para 24
graus de liberdade (gl = n – 1 = 25 – 1 = 24),
para uma área na cauda superior igual a
0,005 (pois o intervalo de confiança é
simétrico, o que obriga a dividir 1% em dois,
resultando 0,5%, 0,005 em valores absolutos),
obtém-se tn-1,crítico = 2,797
Basta agora substituir os valores na expressão, para cada linha de produção:
Linha de produção A:
s
8,2279
IC(;99%)A  x  t 
 178,9664  2,797 
 178,9664  4,6027 psi
n
25
Linha de produção B:
s
10,0553
IC(;99%)B  x  t 
 184,142  2,797 
 184,142  5,6249 psi
n
25
Linha de produção C:
s
8,5903
IC(;99%)C  x  t 
 176,6884  2,797 
 176,6884  4,8054 psi
n
25
Mas como os tamanhos das três populações são conhecidos (N = 250), e N é menor do que 20 × n, é
preciso corrigir os valores dos erros dos ICs:
Linha de produção A:
s
Nn
250  25
IC(;99%)A  x  t 

 178,9664  4,6027 
 178,9664  4,3753 psi
N 1
250  1
n
Linha de produção B:
s
Nn
250  25
IC(;99%) B  x  t 

 184,142  5,6249 
 184,142  5,3470 psi
N 1
250  1
n
Linha de produção C:
s
Nn
250  25
IC(;99%) C  x  t 

 176,6884  4,8054 
 176,6884  4,5679 psi
N 1
250  1
n
E as interpretações:
Na linha A, há 99% de probabilidade de que a média populacional da resistência esteja entre
174,5911 e 183,3417 psi.
Na linha B, há 99% de probabilidade de que a média populacional da resistência esteja entre 178,795
e 189,489 psi.
Na linha C, há 99% de probabilidade de que a média populacional da resistência esteja entre
172,1205 e 181,2563 psi.
Observe que o intervalo da linha B apresenta limites inferior e superior acima dos das outras linhas, e
que a linha C apresenta os menores limites. Contudo, existe superposição entre todos eles.
3) O fabricante de bebidas da questão 1 necessita que as garrafas apresentem uma resistência média à
pressão de no mínimo 175 psi. Sabe-se, pela questão 2, que as distribuições das resistências nas
populações podem ser aproximadas pela normal.
a) Aplicando um teste estatístico apropriado, usando 1% de significância e as medidas da questão 1,
responda se as 3 linhas de produção atendem ao requisito.
b) Se a média real fosse de 177 psi, qual seria a probabilidade do teste da letra a detectar isso, supondo
que os desvios padrões amostrais sejam boas estimativas dos desvios padrões populacionais?
c) Se desejássemos que o teste da letra a detectasse que a média real vale 177 psi com 90% de
probabilidade, para 1% de significância, supondo que os desvios padrões amostrais sejam boas
estimativas dos desvios padrões populacionais, qual seria o tamanho mínimo de amostra necessário
para cada linha de produção?
RESOLUÇÃO
a)
Trata-se de uma situação que exige tomada de decisão, obrigando o uso de teste de hipóteses, além
disso, está explicitamente pedido no enunciado para aplicar um teste de hipóteses.
Enunciando as hipóteses:
H0: μ = 175 psi
H1: μ > 175 psi
Está explicitamente dito para testar a média (μ), e o valor de teste é de 175 psi. Se as garrafas
resistirem a mais do que isso, serão aprovadas. Como rejeitar H0 é uma declaração “mais forte” do
que aceitá-la, usamos o maior do que 175 em H1, pois para rejeitar a hipótese a amostra indica que
existem provas estatísticas suficientes para isso (“guilty” no direito penal americano), enquanto que
ao aceitar a hipótese não encontramos provas suficientes para rejeitá-la (“not guilty”).
Trata-se de um teste unilateral à direita, em cada linha as amostras tem 25 elementos (menos do que
30), as variâncias populacionais das resistências nas 3 linhas são desconhecidas (não há informações,
novamente, a respeito), mas as distribuições das resistências podem ser aproximadas por uma normal:
devemos usar a distribuição t de Student com 24 graus de liberdade (gl = n – 1 = 25 – 1 = 24):
x  0
t 24 
s/ n
Linha de produção A:
x   0 178,9664  175
t 24 

 2,410
s/ n
8,2279 / 25
Linha de produção B:
x  0 184,142  175
t 24 

 4,546
s / n 10,0553 / 25
Linha de produção C:
x  0 176,6884  175
t 24 

 0,983
s/ n
8,5903 / 25
Como os testes são unilaterais à direita é preciso calcular a probabilidade de que t 24 seja
maior do que os valores calculados, e comparar com 1% (0,01). Procurando na tabela da distribuição
t de Student para 24 graus de liberdade.
Linha A
Área na cauda superior
0,025
?
0,01
Valor de t24
2,064
2,410
2,492
Como t24 = 2,410, entre 2,064 e 2,492, significa que:
0,01 < P(t24> 2,410) < 0,025, e, portanto, MAIOR do que 0,01 (nível de significância),
indicando que H0 deve ser ACEITA. Interpretação: não há prova estatística suficiente de que a
resistência média das garrafas da linha A seja maior do que 175 psi.
Veja a figura abaixo para maior esclarecimento:
A probabilidade de que t24 seja maior do que 2,410 vale 0,012, portanto maior do que o nível
de significância de 1% (0,01), levando à aceitação de H0. Note, porém, que é um caso de
fronteira, pois o valor é apenas um pouco maior do que 0,01.
Linha B
Área na cauda superior
0,0005
?
Valor de t24
3,745
4,546
Como t24 = 4,546, acima de 3,745, significa que:
P(t24 > 4,546) < 0,0005, e, portanto, MENOR do que 0,01 (nível de significância),
indicando que H0 deve ser REJEITADA. Interpretação: há prova estatística suficiente de que a
resistência média das garrafas da linha B seja maior do que 175 psi.
Veja a figura abaixo para maior esclarecimento:
A probabilidade de que t24 seja maior do que 4,546 vale 0,0001, portanto menor do que o nível
de significância de 1% (0,01), levando à rejeição de H0. E rejeita-se com bastante folga, pois a
probabilidade é mais de cem vezes menor do que 0,01.
Linha C
Área na cauda superior
0,25
?
0,10
Valor de t24
0,685
0,983
1,318
Como t24 = 0,983, entre 0,685 e 1,318, significa que:
0,10 < P(t24> 0,983) < 0,25, e, portanto, MAIOR do que 0,01 (nível de significância),
indicando que H0 deve ser ACEITA. Interpretação: não há prova estatística suficiente de que a
resistência média das garrafas da linha C seja maior do que 175 psi.
Veja a figura abaixo para maior esclarecimento:
A probabilidade de que t24 seja maior do que 0,983 vale 0,1677, portanto muito maior do que o
nível de significância de 1% (0,01), mais de dez vezes, levando à aceitação de H0.
b)
Na prática (LE-3) deveríamos usar a distribuição t de Student não central, mas uma aproximação
razoável para calcular o poder do teste pode ser feita pela t de Student “comum” (central).
Para as três linhas de produção as hipóteses, níveis de significância e tamanhos de amostra são os
mesmos, mudando apenas os desvios padrões. E as hipóteses foram:
H0: μ = 175 psi
H1: μ > 175 psi
Trata-se de um teste unilateral à direita, com valor de teste μ0 = 175. Então os valores de tc (valor de t
acima do qual rejeitaríamos H0, pois é um teste unilateral À DIREITA) serão os mesmos para as três
linhas: procurando na tabela t de Student, para 24 graus de liberdade e área na cauda superior igual
a 0,01, obtemos tc = 2,492. Considerando os desvios padrões amostrais como bons estimadores dos
desvios padrões populacionais, podemos encontrar os valores críticos de médias amostrais,
correspondentes a tc:
Linha de produção
Valor crítico de média amostral
σ≅s
A
8,2279
sA
8,2279
 175  2,492 
 179,101
n
25
B
10,0553
s
10,0553
x cB  0  t c  B  175  2,492 
 180,012
n
25
C
8,5903
s
8,5903
x cC  0  t c  C  175  2,492 
 179,281
n
25
Agora precisamos calcular o valor de t, ou seja, o valor correspondente à média amostral crítica na
distribuição suposta real da resistência, que apresenta média igual 177 psi. O poder do teste será a
probabilidade de que t seja MAIOR do que t, pois é um teste UNILATERAL à direita com região de
rejeição da hipótese H0 à direita, portanto acima da média amostral crítica (correspondente a tc). Mas
que precisa ser calculado na distribuição que tem média “real” igual a 177 psi.
Linha de produção
t
A
x   179,101  177
t A  cA

 1,277
sA / n 8,2279 / 25
B
x   180,012  177
t B  cB

 1,498
s B / n 10,0553 / 25
C
x   179,281  177
t C  cC

 1,328
sC / n 8,5903 / 25
x cA  0  t c 
Como t tem 24 graus de liberdade, e o teste é unilateral à direita, o poder do teste será P(t 24> t),
procurando na tabela da t de Student para 24 graus de liberdade:
Linha A
Área na cauda superior
0,25
?
0,10
0,685
1,277
1,318
Valor de t
Como t = 1,277, entre 0,685 e 1,318, significa que:
0,10 < Poder do teste = P(t24 > 1,277) < 0,25.
Linha B
Área na cauda superior
0,10
?
0,05
1,318
1,498
1,711
Valor de t
Como t = 1,498, entre 1,318 e 1,711, significa que:
0,05 < Poder do teste = P(t24 > 1,498) < 0,10.
Linha C
Área na cauda superior
0,10
?
0,05
1,318
1,328
1,711
Valor de t
Como t = 1,328, entre 1,318 e 1,711, significa que:
0,05 < Poder do teste = P(t24 > 1,328) < 0,10.
Note que são valores pequenos, indicando provavelmente que a amostra deveria ser maior para a
diferença exigida (2 psi acima de μ0). Apenas para referência, os valores do poder do teste para as três
linhas de produção pela distribuição t não central foram 11,93%, 8,28% e 11%, respectivamente, e os
obtidos pela aproximação foram 10,69%, 7,36% e 9,83%, respectivamente.
c)
Usando a expressão de cálculo de tamanho de amostra para testes de hipóteses unilaterais, para caso
de variância populacional desconhecida:
t
t

  0

n 0   n 0 1; n 0 1;  e
s



Todas as amostras piloto têm 25 elementos, então t terá 24 graus de liberdade (gl = n – 1 = 25 – 1 =
24). O nível de significância () vale 0,01(1%), e o poder do teste vale 0,9 (90%) para uma média real
de 177 psi. Procurando na tabela da distribuição t de Student para 24 graus de liberdade, para área
na cauda superior igual a 0,01 e 0,1 (1-0,9), encontramos:
tn0-1; = t24;0,01 = 2,492
e
tn0-1; = t24;0,1 = 1,318
Independente do tipo de teste é IMPERATIVO que os dois valores tenham o mesmo sinal para que se
somem na expressão de cálculo do tamanho de amostra.
Os valores de  para as linhas de produção:
  0 177  175
  0 177  175
  0 177  175
A 

 0,2431 B 

 0,1989 C 

 0,2328
sA
8,2279
sB
10,0553
sC
8,5903
Linha A:
2
t
t
  2,492  1,318 
n 0   n 0 1; n 0 1;   
  245,629  246


  0,2431 
2
2
Linha B:
t
t
  2,492  1,318 
n 0   n 0 1; n 0 1;   
  366,927  367


  0,1989 
2
2
Linha C:
t
t
  2,492  1,318 
n 0   n 0 1; n 0 1;   
  267,845  268


  0,2328 
2
2
Como conhecemos os tamanhos das populações (250 nas três linhas), e dois tamanhos de amostra são
maiores do que os das populações, é preciso fazer a correção:
Linha A:
N  n 0 250  246
n

 123,992  124
N  n 0 250  246
Linha B:
N  n 0 250  367
n

 148,703  149
N  n 0 250  367
Linha C:
N  n 0 250  268
n

 129,344  130
N  n 0 250  268
Para 177 psi, que está próxima da média testada (175 psi), para uma significância de 1% e poder do
teste de 90% (90% de probabilidade de detectar que a média real da resistência NÃO é 175, mas sim
177 psi), precisaríamos de amostras bem maiores do que as retiradas originalmente (no mínimo 4,96
vezes mais...).
4) Imagine que as garrafas da questão 1 são avaliadas qualitativamente como defeituosas ou não
defeituosas. Uma amostra aleatória de 250 garrafas foi retirada de um lote de 4000. Foram encontradas
41 defeituosas na amostra.
a) Obtenha o intervalo de 95% de confiança para a proporção populacional de garrafas defeituosas.
b) Para uma confiança de 95% e precisão de 3% encontre o tamanho mínimo necessário de amostra,
usando a proporção amostral encontrada e através da estimativa exagerada.
RESOLUÇÃO
a)
Está declarado textualmente para obter intervalo de confiança de proporção. Mas o primeiro passo é
avaliar se é possível aproximar a distribuição da proporção amostral de garrafas defeituosas por uma
normal.
Considerando “sucesso” garrafa defeituosa, das quais há 41 na amostra de 250, resulta que
“fracasso” será garrafa não defeituosa, das quais há 209 na amostra de 250. Então:
41
209
p̂ 
 0,164 e 1  p̂ 
 0,836
250
250
Verificando as condições para aproximação pela normal:
n 0  p̂  250  0,164  41
n 0  (1  p̂)  250  0,836  209
Como AMBOS são maiores ou iguais a 5 é possível aproximar a distribuição da proporção amostral
por uma normal, e usar a expressão abaixo:
p̂  (1  p̂)
IC(p;95%)  p̂  Z 
n
Como a amostra tem 250 elementos, o intervalo tem que ter 95% de confiança, podemos encontrar o
valor de Z, Z,crítico, para a expressão acima, e usá-lo para determinar o intervalo:
Por ser um intervalo de confiança
bilateral a significância, 5% (100% - 95% =
5%), 0,05 em valor absoluto, precisa ser
dividida igualmente em duas partes: 0,025 na
cauda superior e 0,025 na inferior. Procuramos
então por Zcrítico, tal que P(Z>Zcrítico) = 0,025.
Pela tabela da distribuição normal padrão
encontramos Zcrítico = 1,96.
Substituindo todos os valores na
expressão do intervalo de confiança:
p̂  (1  p̂)
0,164  0,836
 0,164  1,96 
 0,164  0,046
n
250
Mas como o tamanho da população é conhecido (N = 4000), e N é menor do que 20 × n, é preciso
corrigir o valor do erro do IC:
p̂  (1  p̂)
Nn
0,164  0,836
4000  250
IC(p;95%)  p̂  Z 

 0,164  1,96 

 0,164  0,044
n
N 1
250
4000  1
Interpretação:
Há 95% de probabilidade de que a proporção populacional de garrafas defeituosas esteja entre 0,12
(12%) e 0,208 (20,8%).
IC(p;95%)  p̂  Z 
b)
Exige-se uma confiança de 95%, portanto significância de 5%, com precisão (erro máximo) de 3%
(0,03 em valor absoluto) para o intervalo de confiança da proporção de garrafas defeituosas. O valor
de Z será o mesmo do item a, pelas mesmas razões.
Usando os dados da amostra piloto:
2
Z
 p̂  (1  p̂) 1,962  0,164  0,836
n 0  crítico

 585,221  586
2
0,032
E0
Como o tamanho da população é conhecido:
N  n 4000  586
n

 511,121  512
N  n 4000  586
Usando a estimativa exagerada, em que a proporção amostral é igual a 0,5:
2
Zcrítico  p̂  (1  p̂) 1,962  0,5  0,5
n0 

 1067,111  1068
2
0,032
E0
Como o tamanho da população é conhecido:
N  n 4000 1068
n

 842,936  843
N  n 4000  1068
Usando os dados da amostra piloto no mínimo 512 elementos para 95% de confiança e precisão de 3%
para estimar a proporção populacional. Usando a estimativa exagerada o tamanho mínimo de
amostra sobe para 843.
5) Aplicando um teste estatístico apropriado, usando 1% de significância e as medidas da questão 1, há
evidência de diferença entre as médias de resistência das garrafas das linhas B e C? E entre A e C?
Trata-se de uma situação que exige tomada de decisão, obrigando o uso de teste de hipóteses, além
disso, está explicitamente pedido no enunciado para aplicar um teste de hipóteses, no caso teste de
diferença entre médias. Primeiro mostramos o procedimento para as linhas B e C
Enunciando as hipóteses para as linhas B e C :
H0: μB = μC
H1: μB ≠ μC
Está explicitamente dito para testar as médias (μ).
Trata-se de um teste bilateral, em cada linha as amostras tem 25 elementos (menos do que 30), as
variâncias populacionais das resistências nas duas linhas são desconhecidas (não há informações,
novamente, a respeito), mas as distribuições das resistências podem ser aproximadas por uma normal:
devemos usar a distribuição t de Student com 48 graus de liberdade (gl = nB + nC – 2 = 25 + 25 – 2 =
48), e como as amostras têm o mesmo tamanho:
2
2
s B  sC
n
2
s

t 48  x B  x C 
e
a
2
2
2  sa
Substituindo os valores nas expressões:
2
2
s  sC 10,05532  8,59032
2
sa  B

 87,4511
2
2
n
25
t 48  x B  x C  
 (184,142  176,6884) 
 2,818
2
2  87,4511
2  sa
Como o teste é bilateral é preciso calcular a probabilidade de que t48 seja maior do que os
valores calculados, multiplicar esta probabilidade por 2, e comparar com 1% (0,01). Procurando na
tabela da distribuição t de Student para 48 graus de liberdade (podemos aproximar por 50 graus de
liberdade).
Área na cauda superior
0,005
?
0,0025
Valor de t48
2,678
2,818
2,937
Como t48 = 2,818, entre 2,678 e 2,937, significa que:
0,0025×2 < P(t48> 2,818) < 0,005×2, ou seja, 0,005 < < P(t48> 2,818) < 0,01, e, portanto,
MENOR do que 0,01 (nível de significância), Indicando que H0 deve ser REJEITADA.
Interpretação: há prova estatística suficiente de que as resistências médias das garrafas
das linhas B e C sejam diferentes.
Veja a figura abaixo para maior esclarecimento:
A probabilidade de que t48 seja maior do que 2,818 vale 0,0035, multiplicando-a por 2 resulta
0,007, portanto abaixo do nível de significância de 1% (0,01), levando à rejeição de H0.
Enunciando as hipóteses para as linhas A e C :
H0: μA = μC
H1: μA ≠ μC
Está explicitamente dito para testar as médias (μ).
Trata-se de um teste bilateral, em cada linha as amostras tem 25 elementos (menos do que 30), as
variâncias populacionais das resistências nas duas linhas são desconhecidas (não há informações,
novamente, a respeito), mas as distribuições das resistências podem ser aproximadas por uma normal:
devemos usar a distribuição t de Student com 48 graus de liberdade (gl = nA + nC – 2 = 25 + 25 – 2 =
48), e como as amostras têm o mesmo tamanho:
2
2
n
s A  sC
2
sa 
t 48  x A  x C  
e
2
2
2  sa
Substituindo os valores nas expressões:
2
2
sA  sC
8,2279 2  8,59032
2
sa 

 70,746
2
2
n
25
t 48  x A  x C  
 (178,9664  176,6884) 
 0,958
2
2  70,746
2  sa
Como o teste é bilateral é preciso calcular a probabilidade de que t48 seja maior do que os
valores calculados, multiplicar esta probabilidade por 2, e comparar com 1% (0,01). Procurando na
tabela da distribuição t de Student para 48 graus de liberdade (podemos aproximar por 50 graus de
liberdade).
Área na cauda superior
0,25
?
0,10
Valor de t48
0,679
0,958
1,299
Como t48 = 0,958, entre 0,679 e 1,299, significa que:
0,10×2 < P(t48> 0,958) < 0,25×2, ou seja, 0,2 < P(t48> 0,958) < 0,50, e, portanto, MAIOR do
que 0,01 (nível de significância), indicando que H0 deve ser ACEITA. Interpretação: não há
prova estatística suficiente de que as resistências médias das garrafas das linhas A e C sejam
diferentes.
Veja a figura abaixo para maior esclarecimento:
A probabilidade de que t48 seja maior do que 0,958 vale 0,1714, multiplicando-a por 2 resulta
0,3428, portanto bem maior do que o nível de significância de 1% (0,01), levando à aceitação
de H0.
Observem que os testes corroboram as análises exploratórias feitas na questão 1, letra c.