Notas de Aula #3 (14/10/16) - SOL

01
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE GOIÁS
DEPARTAMENTO DE MATEMÁTICA E FÍSICA
Disciplina: FÍSICA GERAL E EXPERIMENTAL I (MAF 2201)
Prof. EDSON VAZ
NOTA DE AULA III
– ENERGIA CINÉTICA E TRABALHO
Em nosso cotidiano usamos várias formas de energia. Energia é uma grandeza escalar
difícil de ser definida, no entanto, sabemos que em um sistema isolado a quantidade total de
energia permanece a mesma, ou seja, a energia pode ser transformada de uma forma para
outra ou transferida de um objeto para outro, mas sempre será conservada.
ENERGIA CINÉTICA (K)
A energia cinética é a energia associada ao estado de movimento de um objeto.
Quanto mais rapidamente um objeto estiver se movendo, maior será sua energia cinética e
quando o objeto está em repouso, sua energia cinética é nula.
Para um objeto de massa m cuja velocidade v é bem inferior à velocidade da luz,
definimos a sua energia cinética como
K = ½ mv2
A unidade no SI para a energia cinética (e todos os outros tipos de energia) é o joule (
J ), em homenagem a James Prescott Joule, um cientista inglês do século XIX.
TRABALHO
No cotidiano a palavra trabalho geralmente está relacionada ao desempenho de alguma
tarefa ou serviço que exigem esforços físicos ou mentais. Na Física, entretanto, este termo é
usado num sentido mais específico, que envolve a aplicação de uma força a um corpo e o
deslocamento deste corpo.
O trabalho está relacionado à energia transferida para um objeto, ou extraída dele,
através de uma força que atua sobre o objeto. Quando a energia é transferida para o objeto
dizemos que o trabalho realizado pela força é positivo, e quando a energia é extraída do objeto
dizemos que o trabalho negativo. O trabalho possui a mesma unidade que energia e é uma
grandeza escalar.
TRABALHO DE UMA FORÇA CONSTANTE SOBRE UM OBJETO QUE SE MOVE EM
UMA DIMENSÃO
Inicialmente estudaremos o trabalho realizado por forças constantes. Na figura abaixo
está representado o deslocamento ( d ) de um objeto (considerado como uma partícula) e uma
força constante ( F ) que atua neste objeto. O trabalho realizado pela força F durante o
deslocamento d é dado pelo produto escalar entre a força e o deslocamento
F

d
02
W  F.d  W  Fd cos
Usando a definição de produto escalar entre dois vetores, percebemos que o trabalho é
uma grandeza escalar que pode ser positivo, negativo ou nulo, dependendo do ângulo entre a
força e o deslocamento. Quando a força possui uma componente na mesma direção e sentido
que o deslocamento, o trabalho realizado por ela é positivo. Se o sentido da componente da
força for oposto ao deslocamento, o trabalho será negativo. Se a força for perpendicular ao
deslocamento, ela não terá componente na direção do deslocamento e o trabalho será nulo.
Quando duas ou mais forças atuam sobre um objeto, o trabalho total realizado sobre
o objeto pode ser calculado pela soma algébrica dos trabalhos individuais realizados por cada
uma das forças ou pelo trabalho realizado pela força resultante que atua no objeto.
TEOREMA DO TRABALHO-ENERGIA CINÉTICA
A variação da energia cinética de uma partícula é igual ao trabalho total realizado
sobre a partícula, ou seja, o trabalho realizado pela força resultante sobre uma partícula é igual
à variação da energia cinética desta partícula
W  K  W 
1 2 1 2
mv  mv0
2
2
Se o trabalho total realizado sobre uma partícula for positivo, então a energia cinética
da partícula aumenta de uma quantidade igual a este trabalho. Se o trabalho total for negativo,
então a energia cinética da partícula diminui de uma quantidade igual ao trabalho.
O teorema do trabalho-energia cinética vale também quando a força resultante não for
constante, ou seja, quando a força resultante sofrer variação durante o deslocamento.
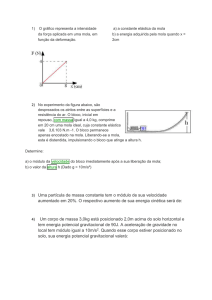
1.
2.
Exercícios:
O Trabalho realizado por uma força constante F sobre uma partícula, durante um
deslocamento em linha reta d será positivo ou negativo se (a) o ângulo entre F e d for de
30º; (b) o ângulo for de 100º; (c) F = 2iˆ - 3jˆ e d = -4iˆ ?
Na figura abaixo, um porco ensebado pode escolher uma dentre três rampas lisas para
escorregar em direção ao solo. Classifique as rampas de acordo com a quantidade de
trabalho que a força gravitacional realiza sobre o porco durante a descida, da maior para a
menor.
03
-31
kg) possui uma energia cinética de 6,7 x 10-19 J,
3.
Se um elétron (massa m = 9,11 x 10
qual é a velocidade do elétron?
4.
Calcule as energias cinéticas dos seguintes objetos se movendo nas velocidades dadas: (a)
um zagueiro de futebol americano de 110 kg correndo a 8,1 m/s; (b) uma bala de 4,2 g a
950 m/s; (c) o porta-aviões Nimitz, de 91.400 ton a 32 nós ( 1 nó = 1,852 km/h).
5.
Um pai apostando corrida com seu filho tem a metade de energia cinética do filho, que
possui metade da massa do pai. O pai aumenta sua velocidade de 1,0 m/s e então passa a
ter a mesma energia cinética do filho. Quais são as velocidades originais (a) do pai e (b)
do filho?
6.
Um bloco de gelo flutuante é empurrado sobre um deslocamento d = (15m)iˆ - (12m)jˆ ao
longo de um dique reto por uma descarga de água, que exerce uma força
F = (210N)iˆ - (150N)jˆ sobre o bloco. Quanto trabalho a força realiza sobre o bloco durante o
deslocamento?
7.
Para puxar um caixote de 50 kg em um piso horizontal sem atrito, um trabalhador aplica
uma força de 210 N, fazendo um ângulo de 20º para cima medido a partir da horizontal.
Quando o caixote se move 3,0 m, qual o trabalho realizado sobre o caixote (a) pela força
do trabalhador, (b) pela força gravitacional que atua sobre o caixote e (c) pela força
normal que o piso exerce sobre o caixote? (d) Qual é o trabalho total realizado sobre
caixote?
8.
Uma força resultante age sobre um objeto de 3,0 kg, que pode ser tratado como uma
partícula, de tal forma que a posição do objeto em função do tempo é dada por x = 3,0t –
4,0t2 + 1,0t3, com x em metros e t em segundos. Determine o trabalho realizado sobre o
objeto pela força de t = 0 até t = 4,0s. (Sugestão: Quais são as velocidades nesses
tempos?)
9.
A figura abaixo mostra três forças aplicadas a um baú que se move para a esquerda por
3,0 m sobre um piso sem atrito. Os módulos das forças são F1 = 5,00N, F2 = 9,00 N e F3 =
3,00 N. Durante o deslocamento, (a) qual é o trabalho resultante que as três forças
realizam sobre o baú, e (b) a energia cinética do baú aumenta ou diminui?
04
10.
A figura abaixo mostra uma vista superior de três forças horizontais agindo sobre uma
caixa de carga que estava inicialmente em repouso, mas que agora se move em um piso
sem atrito. As intensidades das forças atuantes são F1 = 3,00 N, F2 = 4,00 N e F3 = 10,0 N.
Qual é o trabalho resultante realizado sobre a caixa pelas três forças durante os primeiros
4,00 m de deslocamento?
11.
Na figura abaixo uma corda passa por duas roldanas de massas e atrito desprezíveis; uma
lata cilíndrica metálica de massa m = 20 kg está pendurada em uma das roldanas. Se você
exercer uma força F sobre a extremidade livre da corda, (a) qual deve ser a intensidade de
F a fim de que a lata seja suspensa com velocidade constante? (b) Para suspender a lata
2,0 cm, quantos centímetros você deve puxar a extremidade livre da corda? Durante esse
levantamento, qual é o trabalho realizado sobre a lata (c) pela sua força (transmitida via
corda) e (d) pela força gravitacional sobre a lata? (Sugestão: Quando uma corda passa em
volta de uma roldana como mostrado, ela puxa a roldana com uma força resultante que é o
dobro da tração na corda.)
12.
Um bloco de gelo de 45 kg desce deslizando um plano inclinado liso de 1,5 m de
comprimento e 0,91 m de altura. Um trabalhador aplica uma força para cima contra o
bloco de gelo na direção paralela ao plano inclinado, para que o bloco desça deslizando
com velocidade constante. (a) Encontre a intensidade da força do trabalhador. Quanto
trabalho é realizado sobre o bloco (b) pela força do trabalhador, (c) pela força
gravitacional, (d) pela força normal à superfície do plano inclinado e (e) pela força
resultante?
13.
Um helicóptero eleva uma astronauta de 72 kg verticalmente por 15 m a partir do oceano
por meio de um cabo. A aceleração da astronauta é g/10. Quanto trabalho é realizado
sobre a astronauta (a) pela força do helicóptero e (b) pela força gravitacional agindo sobre
ela? Quais são (c) a energia cinética e (d) a velocidade da astronauta imediatamente antes
de ela alcançar o helicóptero?
05
14.
Uma corda é usada para abaixar verticalmente um bloco de massa M, inicialmente em
repouso, com uma constante aceleração para baixo de g/4. Quando o bloco tiver caído
uma distância d, encontre (a) o trabalho realizado pela força da corda sobre o bloco, (b) o
trabalho realizado pela força gravitacional sobre o bloco, (c) a energia cinética do bloco e
(d) a velocidade do bloco.
TRABALHO REALIZADO POR UMA FORÇA VARIÁVEL: EM UMA DIMENSÃO
Para uma força constante e de mesma direção e sentido do deslocamento é fácil
verificar que o trabalho realizado por ela é numericamente igual a “área sob a curva” no
gráfico F  x , como está representado na figura abaixo. Mesmo quando o valor da força
estiver variando esta propriedade é válida, sendo que o trabalho de uma força variável na
direção x pode ser calculado por
x2
w
 F ( x) dx
x1
F(x)
w
x1
x2
Para uma força tridimensional F  Fxiˆ  Fy ˆj  Fz kˆ onde Fx depende apenas da
posição x, e Fy depende apenas de posição y, e Fz depende apenas a posição z, o trabalho é
dado por
W
xF
yF
xi
yi
 Fx d x 

zF
Fy d y   Fz d z
zi
TRABALHO REALIZADO PELA FORÇA ELÁSTICA DE UMA DE MOLA
A seguir iremos examinar o trabalho realizado sobre um corpo pela força exercida por
uma mola.
A força exercida por uma mola ideal é diretamente proporcional à distância através da
qual ela é esticada ou comprimida. A força exercida pela mola pode, portanto, ser expressa
em termos de distância x, através da qual ela é esticada ou comprimida, a partir do seu
comprimento de equilíbrio, por
F  kx (Lei de Hooke)
O sinal negativo indica que a força da mola tem sempre sentido contrário ao
deslocamento. A constante K é chamada de constante da mola e é uma medida da rigidez da
mola.
Vamos calcular o trabalho realizado por uma mola sobre uma partícula deslocando-se
horizontalmente de uma posição inicial xi até uma posição final xf. Como a força da mola é
variável o trabalho pode ser calculado por
06
W
xF
 F ( x) dx 
xi
xF
x
F
1
1
2
2
2
2

kx
dx


k
xi
xi xdx   2 k ( x f  xi )  2 k ( xi  x f )
Exercícios:
15. A figura abaixo apresenta quatro gráficos (desenhados na mesma escala) da componente x
de uma força variável F (na direção do eixo x) contra a posição x de uma partícula sobre a
qual a força atua. Classifique os gráficos de acordo com o trabalho realizado pela força F
sobre a partícula de x = 0 até x1, do trabalho mais positivo para o trabalho mais negativo.
16.
Uma mola com constante de mola de 15 N/cm tem uma gaiola presa a uma das suas
extremidades. (a) Quanto trabalho a força da mola realiza sobre a gaiola quando a mola
for esticada de 7,6 mm a partir da sua posição não deformada? (b) Quanto trabalho
adicional será realizado pela força da mola quando a mola for esticada outros 7,6 mm?
17.
Um bloco de 250 g é solto sobre uma mola vertical não deformada que possui uma
constante de mola k= 2,5 N/cm (figura abaixo). O bloco passa a ficar preso à mola
comprimindo-a 12 cm antes de parar por um instante. Enquanto a mola estiver sendo
comprimida, qual é o trabalho realizado sobre o bloco (a) pela força gravitacional que age
sobre ele e (b) pela força da mola? (c) Qual é a velocidade do bloco imediatamente antes
de ele acertar a mola? (Suponha que o atrito seja desprezível.) (d) Se a velocidade no
impacto for duplicada, qual será a compressão máxima da mola?
07
18.
A única força atuante sobre um corpo de 2,0 kg enquanto ele se move ao longo do sentido
positivo do eixo x possui uma componente x igual a FX = -6X N, onde x está em metros. A
velocidade do corpo em x = 3,0 m é de 8,0 m/s. (a) Qual a velocidade do corpo em x = 4,0
m? (b) Em qual valor positivo de x o corpo terá uma velocidade de 5,0 m/s?
19.
Um bloco de 5,0 kg se move em linha reta sobre uma superfície horizontal lisa sob a
influência de uma força que varia com a posição, com mostrado na figura abaixo. Quanto
trabalho está força realiza para mover o bloco da origem até a posição x = 8,0 m?
20.
A força sobre uma partícula está dirigida ao longo de um eixo x e é dada por
F = F0 [(x/x0 ) -1]. Determine o trabalho realizado pela força ao mover a partícula de x = 0
até x = 2x0, (a) Fazendo o gráfico (F × x) e medindo o trabalho a partir do gráfico e (b) por
integração de F(x).
21.
Qual o trabalho realizado por uma força F = (2xN)iˆ + (3N)jˆ , com x em metros, que desloca
uma partícula da posição ri = (2m)iˆ + (3m)jˆ para uma posição rf = -(4m)iˆ - (3m)jˆ ?
POTÊNCIA
A potência devido a uma força é a taxa com que essa força realiza trabalho sobre um
objeto, ou seja, a potência está relacionada à rapidez com que esta força realiza trabalho. Se a
força realiza um trabalho W durante um intervalo de tempo é Δt, a potência média neste
intervalo de tempo é
Pm 
W
t
A potência instantânea P é a taxa instantânea de realização de trabalho, que pode ser
escrita como a derivada do trabalho em relação ao tempo
dW
P
dt
A unidade de potência no SI é o joule por segundo, chamado de watt (W).
O nome da unidade de potência é em homenagem a James Watt, o qual aperfeiçoou
consideravelmente a taxa com que as máquinas a vapor conseguiam realizar trabalho.
1
joule
 1 watt  1W
segundo
08
Também podemos expressar a potência instantânea com que uma força realiza
trabalho sobre uma partícula (ou um corpo que se comporta como uma partícula) em termos
dessa força e da velocidade instantânea da partícula. Para uma partícula que esteja se
movendo em linha reta (por exemplo, no eixo x) e sofra ação de uma força constante F na
direção que faz um ângulo  com esta linha, temos que
P
dW F cos  dx
 dx 

 F cos   
dt
dt
 dt 

 P  Fv cos
P  F .v
Portanto, a potência instantânea com que a força F realiza trabalho sobre uma
partícula é dada pelo produto escalar entre a força e a velocidade instantânea da partícula.
22.
23.
Exercícios:
A cabine carregada de um elevador possui uma massa de 3,0 x 103 kg sobe 210 m em 23s
com velocidade constante. Qual é a taxa média de trabalho realizado pela força do cabo do
elevador sobre a cabine?
Um bloco de 100 kg é puxado com velocidade constante de 5,0 m/s sobre um piso
horizontal por uma força aplicada de 122 N que forma um ângulo de 37º em relação ao
plano horizontal. Qual a taxa com que a força realiza trabalho sobre o bloco?
ENERGIA POTENCIAL E CONSERVAÇÃO DA ENERGIA
Antes de introduzirmos o conceito de Energia Potencial vamos discutir o conceito de
Forças Conservativas.
Forças Conservativas
Para uma força conservativa, o trabalho total que ela realiza sobre uma partícula se
movendo ao longo de qualquer percurso fechado é nulo, ou seja, o trabalho total realizado por
uma força conservativa sobre uma partícula, partindo de um ponto inicial e depois voltando a
esse mesmo ponto (fazendo uma viagem de ida e volta) é nulo.
Temos uma propriedade muito importante relacionada às forças conservativas: O
trabalho realizado por uma força conservativa sobre uma partícula se movendo entre dois
pontos não depende da trajetória seguido pela partícula.
A força gravitacional e a força elástica de mola são exemplos de forças conservativas.
A força de atrito cinético é uma força não-conservativa.
Energia Potencial
A energia potencial está associada à configuração de um sistema no qual atua uma
força conservativa. Quando a força conservativa realiza um trabalho W sobre uma partícula
dentro de um sistema, a variação da energia potencial U do sistema é igual a menos o
trabalho realizado.
U  W
09
Energia Potencial Gravitacional
Temos vários tipos de energia potencial, mas neste momento vamos discutir dois tipos
específicos, a energia potencial gravitacional e a energia potencial elástica.
A energia potencial associada a um sistema formado pela Terra e por uma partícula
próxima à superfície da terra é a energia potencial gravitacional. Se a partícula se move de
uma altura inicial hi para a altura final hf, a variação da energia potencial gravitacional do
sistema partícula-Terra é
U  mg (h f  hi )  mg h
Devemos observar que fisicamente o que importa é a variação de energia, mas é
comum nos referirmos a um determinado valor para a energia potencial gravitacional de um
sistema partícula-Terra quando a partícula está a uma altura h em relação a um determinado
ponto de referência. Se considerarmos U i  0 como sendo a energia potencial gravitacional
do sistema quando este se encontra em uma configuração de referência na qual a partícula está
em um ponto de referência hi  0 , a energia potencial gravitacional U quando a partícula
está em qualquer altura h é
U  mgh .
Portanto, a energia potencial gravitacional associada a um sistema partícula-Terra
depende da altura da partícula em relação à posição de referência h = 0. Observe que a
diferença entre as energias potenciais gravitacionais não depende da posição de referência.
Energia Potencial Elástica
A energia potencial elástica é a energia associada ao estado de compreensão ou
alongamento de um objeto elástico. Para um sistema massa-mola, no qual uma mola exerce
sobre um bloco a força F  kx quando a mola sofre uma deformação x, a energia potencial
elástica do sistema massa-mola é dada por
U
1 2
kx
2
Para este caso a configuração de referência corresponde à mola na sua posição não
deformada, na qual x = 0 e U  0 .
Mesmo a energia potencial sendo associada a um sistema como um todo, na prática é
comum associarmos esta energia apenas a uma parte do sistema. Afirmações do tipo a energia
potencial gravitacional de um corpo é de 20J é aceitável, mas devemos ter sempre em mente
que a energia potencial gravitacional está associada ao sistema objeto-Terra.
Energia Mecânica
A energia mecânica E de um sistema é a soma da sua energia cinética k com a sua
energia potencial U .
E  k U
Princípio da Conservação da Energia Mecânica
010
Em um sistema isolado onde apenas forças conservativas realizam trabalho (causam
variações de energia), a energia cinética e a energia potencial podem variar, mas a sua soma, a
energia mecânica, não se altera. Ou seja, a energia mecânica de um sistema isolado, onde
atuam somente forças conservativas, se conserva.
Ei  E f  Ki  U i  K f  U f
Podemos pensar no movimento de um pêndulo ou num sistema massa-mola, nos
quais são desprezados os atritos e a resistência do ar, para discutir a conservação da energia
mecânica. Nestes casos temos transformações de energia cinética em potencial e de energia
potencial em cinética de tal maneira que a soma das duas (a energia mecânica) sempre
permanece constante.
Exercícios:
24. Qual a constante de mola de uma mola que armazena 25 J de energia potencial elástica
quando comprimida 7,5 cm a partir do seu comprimento não deformado?
25.
Você deixa cair um livro de 2,00 kg para um amigo que está em pé, 10,0 m abaixo do
livro, com as mãos estendidas 1,50 m acima do chão (figura abaixo). (a) Qual o trabalho
Wg que a força gravitacional realiza sobre o livro enquanto ele cai até chegar nas mãos do
seu amigo? (b) Qual a variação U da energia potencial gravitacional do sistema livroTerra durante a queda? Se a energia potencial gravitacional U desse sistema for tomada
como nula no nível do solo, qual será o valor de U quando o livro (c) for solto e (d) chegar
às mãos do seu amigo? Considere agora que U seja 100 J no nível do solo e encontre
novamente (e) Wg, (f) U, (g) U no ponto em que o livro é solto e (h) quando o livro
atingir as mãos do seu amigo.
26.
Na figura abaixo, um carro de montanha-russa de massa m chega sem atrito ao alto da
primeira elevação com uma velocidade V0. Quanto trabalho a força gravitacional realiza
sobre ele desse ponto até (a) o ponto A, (b) o ponto B e (c) o ponto C? Se a energia
potencial gravitacional do sistema carro-Terra for tomada como nula no ponto C, qual será
o seu valor quando o carro estiver (d) no ponto B e (e) no ponto A? (f) Se a massa m fosse
duplicada, a variação da energia potencial gravitacional do sistema entre os pontos A e B
aumentaria, diminuiria ou permaneceria a mesma?
011
27.
A figura abaixo mostra uma bola de massa m presa à extremidade de uma haste fina de
comprimento L e massa desprezível. A outra extremidade da haste é pivotada de modo
que a bola possa se mover em um círculo vertical. A haste é mantida na posição horizontal
como mostrado e depois recebe um empurrão para baixo suficiente para fazer com que a
bola gire para baixo e continue a girar no sentido trigonométrico até alcançar exatamente a
posição vertical para cima, ali chegando com velocidade nula. Qual o trabalho realizado
sobre a bola pela força gravitacional do ponto inicial (a) até o ponto mais baixo, (b) até o
ponto mais alto e (c) até o ponto na direita no qual a bola possui o mesmo nível do ponto
inicial? Se tomarmos a energia potencial gravitacional dos sistemas bola-Terra como nula
no ponto inicial, qual será o seu valor quando a bola atingir (d) o ponto mais baixo, (e) o
ponto mais alto e (f) o ponto no lado direito em que a bola está no mesmo nível do ponto
inicial? (g) Suponha que a haste fosse empurrada com mais força de modo que a bola
passasse pelo ponto mais alto com uma velocidade diferente de zero. A variação da
energia potencial gravitacional do ponto mais baixo para o ponto mais alto seria então
maior, menor ou a mesma?
28.
Na figura abaixo, um pequeno bloco de massa m pode deslizar ao longo de um loop sem
atrito. O bloco é solto do repouso no ponto P, a uma altura h = 5R acima da parte mais
baixa do loop. Quanto trabalho a força gravitacional realiza sobre o bloco enquanto o
bloco se desloca do ponto P (a) até o ponto Q e (b) até a parte mais alta do loop? Se a
energia potencial gravitacional do sistema bloco-Terra for tomada como nula na parte
mais baixa do loop, qual será a energia potencial quando o bloco estiver (c) no ponto P,
(d) no ponto Q e (e) no ponto mais alto do loop (f) Se, em vez de ser solto do repouso, o
bloco receber alguma velocidade inicial para baixo ao longo da pista as repostas para os
itens de (a) até (e) aumentam, diminuem ou permanecem as mesmas?
012
29.
(a) No exercício 25, qual a velocidade do livro quando ele atinge as mãos? (b) Se
substituíssemos o livro por outro com o dobro da massa, qual seria sua velocidade? (c) Se,
em vez disso, o livro fosse atirado para baixo, à resposta do item (a) aumentaria,
diminuiria ou permaneceria a mesma?
30.
(a) No exercício 27, que velocidade inicial deve ser dada à bola para que ela alcance a
máxima posição vertical com velocidade nula? Qual é então a sua velocidade (b) no ponto
mais baixo e (c) no ponto no lado direito no qual a bola está no mesmo nível do ponto
inicial? (d) Se a massa da bola fosse dobrada, as respostas correspondentes aos itens (a)
até (c) aumentariam, diminuiriam, ou permaneceriam as mesmas?
31.
No exercício 26, qual a velocidade do carro de montanha-russa (a) no ponto A, (b) no
ponto B e (c) no ponto C? (d) Que altura ele alcançará na última elevação, que é alta
demais para ele cruzar? (e) Se substituirmos o carro por um segundo carro com o dobro da
massa, quais serão então as respostas correspondentes aos itens (a) até (d)?
32.
A figura abaixo mostra uma pedra de 8,00 kg em repouso em cima de uma mola. A mola
está comprimida de 10,0 cm pela pedra. (a) Qual a constante de mola? (b) A pedra é
empurrada para baixo mais 30,0 cm e então é solta. Qual a energia potencial elástica da
mola comprimida imediatamente antes de a pedra ser solta? (c) Qual a variação da energia
potencial gravitacional do sistema pedra-Terra quando a pedra se move do ponto em que
foi solta até a sua altura máxima? (d) Qual será essa altura máxima, medida a partir do
ponto em que a mola é solta?
33.
Uma bola de gude de 5,0 g é disparada para cima na vertical usando-se um revólver de
mola. A mola deve ser comprimida 8,0 cm para que a bola de gude chegue a atingir um
alvo 20 m acima da posição da bola de gude com a mola comprimida. (a) Qual a variação
Ug da energia potencial gravitacional do sistema bola de gude-Terra nos 20 m da subida?
(b) Qual a variação US da energia potencial elástica da mola durante o lançamento da
bola de gude? (c) Qual a constante de rigidez da mola?
34.
Um bloco de 2,00 kg é posicionado contra uma mola sobre um plano inclinado de 30º sem
atrito (figura abaixo, o bloco não está preso à mola.). A mola, cuja constante de elástica é
igual a 19,6 N/cm, é comprimida 20,0 cm e depois solta. (a) Qual a energia potencial
elástica da mola comprimida? (b) Qual a variação da energia potencial gravitacional do
sistema bloco-Terra quando o bloco se move do ponto de onde foi solto até seu ponto
mais alto no plano inclinado? (c) Qual a distância, ao longo do plano inclinado, do ponto
mais alto que o bloco atinge até o ponto de onde ele foi solto?
013
35.
Na abaixo, solta-se um bloco de 12 kg a partir do repouso em uma rampa de 30º sem
atrito. Abaixo do bloco está uma mola que pode ser comprimida 2,0 cm por uma força de
270 N. O bloco pára por um instante ao comprimir 5,5 cm da mola. (a) Que distância o
bloco percorre ao descer a rampa da sua posição de repouso até este ponto de parada? (b)
Qual a velocidade do bloco no exato momento em que ele toca a mola?
36.
Um bloco de 2,0 kg é solto de uma altura de 40 cm sobre uma mola, cuja constante de
mola k é igual a 1960 N/m (figura abaixo). Encontre a distância máxima que a mola foi
comprimida.
Curvas de Energia Potencial
Podemos aprender muito a respeito do movimento de uma partícula a partir de um
gráfico da energia potencial do sistema.
Se conhecermos a função energia potencial U ( x) para um sistema no qual uma força
unidimensional de intensidade F age sobre uma partícula, podemos encontrar esta força pela
equação
F ( x)  
dU ( x)
.
dx
Se tivermos o gráfico de U ( x) , então para qualquer valor de x, a intensidade da força F é
igual a menos o coeficiente angular da reta tangente à curva nesse ponto. Um ponto de
reversão é um ponto x no qual a partícula inverte o sentido do seu movimento (nesse ponto a
energia cinética da partícula é nula). A partícula está em equilíbrio nos pontos onde a
inclinação de U ( x) é nula (nesse ponto, F(x) = 0).
Trabalho realizado por uma força externa sobre um sistema
014
O trabalho de uma força externa W é a energia transferida para um sistema ou retirada
dele por meio de uma força externa atuando sobre o sistema. Quando mais de uma força
externa atua sobre um sistema, o trabalho total delas é igual a esta energia. Quando não há
atrito (força não-conservativa) envolvido, o trabalho realizado sobre o sistema, pelas forças
externas, e a variação da energia mecânica do sistema são iguais:
W  E
Quando uma força de atrito cinético atua dentro do sistema, a energia térmica Ete do
sistema sofre uma variação.
O trabalho realizado sobre o sistema neste caso é igual à soma da variação da energia
mecânica com a variação da energia térmica do sistema:
W  E  Ete
A variação da energia térmica está relacionada com a intensidade da força de atrito f k
e com a intensidade do deslocamento d provocado pela força externa, da seguinte forma:
Ete  Fk .d
Lei da Conservação da Energia
Quando estudamos a conservação da energia mecânica, consideramos apenas as forças
conservativas que atuam no sistema. Se pensarmos no movimento do pêndulo ou no sistema
massa-mola considerando os atritos e a resistência do ar, podemos perceber com certa
facilidade que não temos conservação da energia mecânica (soma da potencial com a
cinética). Nestes casos, ou em qualquer outro caso no qual a energia mecânica não se
conserva, a energia total do sistema se conserva.
Muitas transferências de energia podem acontecer em um sistema isolado, mas não
temos troca de energia entre este sistema e o ambiente externo ao sistema. Portanto, a energia
total (soma de todas as energias) de um sistema isolado se conserva.
Devemos lembrar que a energia mecânica de um sistema isolado se conserva apenas
quando neste sistema atuam somente forças conservativas, mas a energia total de um sistema
isolado se conserva sempre.
Exercícios:
37. A figura abaixo fornece a função energia potencial de uma partícula. (a) Classifique as
regiões AB, BC, CD, DE de acordo com a intensidade da força que age sobre a partícula,
da maior para a menor. Que valor a energia mecânica da partícula EMEC não deve
ultrapassar para que a partícula (b) esteja aprisionada no poço de potencial da esquerda,
(c) esteja aprisionada no poço de potencial da direita e (d) seja capaz de se mover entre
dois poços de potencial mas não para a direita do ponto H? Para a situação do item (d) em
qual das regiões BC, DE, FG a partícula terá (e) sua energia cinética máxima e (f)
velocidade mínima?
015
38.
Na figura abaixo, um bloco desliza ao longo de uma pista que desce uma altura h. A pista
possui atrito desprezível, com exceção da seção mais baixa. Nesta seção, o bloco desliza e
chega ao repouso em uma certa distância D por causa do atrito. (a) Se diminuirmos h, o
bloco agora irá deslizar e chegar ao repouso em uma distância que é maior, menor ou
igual a D? (b) Se, em vez disso, aumentarmos a massa do bloco, a distância de parada será
agora maior, menor ou igual a D?
39.
Na figura abaixo, um bloco desliza de A para C ao longo de uma rampa sem atrito, e
depois passa pela região horizontal CD, onde uma força de atrito atua sobre ele. A energia
cinética ao bloco está aumentando, diminuindo ou se mantendo constante (a) na região
AB, (b) na região BC e (c) na região CD? (d) A energia mecânica do bloco está
aumentando, diminuindo ou permanecendo constante nessas regiões?
40.
Um urso de 25 kg desce a partir do repouso, deslizando 12 m de um tronco de pinheiro,
movendo-se com uma velocidade de 5,6 m/s imediatamente antes de bater no chão. (a)
Que variação ocorre na energia potencial gravitacional do sistema urso-Terra durante a
descida? (b) Qual a energia cinética do urso imediatamente antes de bater no chão? (c)
Qual a força de atrito média que atua sobre o urso enquanto ele desliza?
41.
Uma bala de 30 g, com uma velocidade horizontal de 500 m/s chega ao repouso após
penetrar 12 cm em uma parede sólida. (a) Qual a variação da sua energia mecânica? (b)
Que intensidade da força média exercida pela parede leva a bala ao repouso?
42.
Você empurra um bloco de 2,0 kg contra uma mola horizontal, comprimindo-a por 15 cm.
Você então solta o bloco e a mola faz com que ele deslize sobre o tampo de uma mesa. O
bloco pára a 75 cm do local de onde foi solto. A constante da mola é igual a 200 N/m.
Qual o coeficiente de atrito cinético entre o bloco e a mesa?
43.
Como mostrado na figura abaixo, um bloco de 3,5 kg é acelerado por uma mola
comprimida, cuja constante de mola é igual a 640 N/m. Após se separar da mola, quando
esta retorna ao seu comprimento não deformado, o bloco se desloca sobre uma superfície
horizontal, que possui um coeficiente de atrito cinético de 0,25, por uma distância de 7,8
016
m antes de parar. (a) Qual o aumento da energia térmica do sistema bloco-piso? (b) Qual a
energia cinética máxima do bloco? (c) Qual a redução do comprimento original da mola
antes do bloco começar a se mover?
RESPOSTAS
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
a) positivo; b) negativo; c) negativo.
Todas iguais.
1,2 . 106 m/s.
a) 3608,55 J; b) 1895,25 J; c) 1,24 . 1010 J.
a) 2,41 m/s; b) 4,83 m/s.
4950 J
a) 592 J ; b) 0; c) 0; d) 592 J.
528 J.
a) 1,5 J ; b) aumenta.
15,24 J.
a) 98 N; b) 4 cm; c) 3,9 J ; d) –3,9 J.
a) 265,4 N; b) –398,1 J; c) 398,1 J; d) 0; e) 0.
a) 1,2 . 104 J; b) –1,1 . 104 J; c) 1000 J; d) 5,3 m/s.
Wb > Wa > Wc > Wd.
a) –3 Mgd/4; b) Mgd; c) Mgd/4; d) gd/2 .
a) – 0,043 J; b) – 0,13 J.
a) 0,294 J; b) – 1,8 J; c) 3,47 m/s; d) 0,23m
a) 6,6 m/s ; b) 4,7 m.
25 J.
a) 0; b) 0.
– 6J.
2,68 . 105 W.
487,17 W.
89 N/cm.
a) 166,6 J; b) – 166,6 J; c) 196 J; d) 29,4 J; e) 166,6 J; f) –166,6 J; g) 296 J; h) 129,4 J.
a) 0; b) mgh/2; c) mgh; d) mgh/2; e) mgh; f) aumentaria.
a) mgl; b) –mgl; c) 0; d) –mgl; e) mgl; f) 0; g) seriam as mesmas.
a) 4mgr; b) 3mgr; c) 5 mgr; d) mgr; e) 2 mgr; f) permanecem as mesmas.
a) 12,9 m/s; b) 12,9 m/s; c) aumentaria.
a) 2gl ; b) 2 gl ; c) 2gl ; d) todos permaneceriam as mesmas.
a) V0; b)
2
V 0 + gh ;
c)
2
V 0 + 2gh ;
2
d)
(V0 + 2gh)
; e) as mesmas.
2g
a) 784 N/m; b) 62,72 J; c) 62,72 J; d) 0,8 m.
a) 0,98 J; b) – 0,98 J; c) 306,25 N/m.
a) 39,2 J; b) 39,2 J; c) 4 m.
a) 35 cm; b) 1,7 m/s.
10 cm.
a) FAB > FCD > FBC = FDE; b) 5 J; c) 5 J; d) 6 J; e) FG; f) DE.
a) menor; b) igual.
017
39.
40.
41.
42.
43.
a) aumentando; b) diminuindo; c) diminuindo; d) constantes em AB e BC. Diminuindo em
CD.
a) – 2940 J; b) 392 J; c) 212 N.
a) – 3,75 . 103 J ; b) 3,12 . 104 N.
0,15.
a) 67 J; b) 67 J; c) 46 cm.
RESOLUÇÃO DA LISTA III
1.
T  F.d
ou
T  Fd cos

a)
cos 30º > 0
T>0
b)
cos 100º < 0
c)
T  F .d  2.4  3.0  8 j
T > 0
2.
T  mgh  Ta  Tb  Tc
3.
Ek  6,7.1019 J
1
1
Ek  mv 2  6,7.1019  .9,11.1031.v 2
2
2
6
v  1, 21.10 m / s
4.
a)
1
m  110 kg , v  8,1m / s  Ek  110.(8,1) 2  Ek  3608,55 J
2
b)
1
m  4, 2 g  4, 2.103 kg , v  950 m / s  Ek  .4, 2.103.9502  Ek  1895, 25 J
2
c)
m  91400 ton  9,14.104 ton  9,14.107 kg
v  32 nos  32.1,852 km / h 
32.1,852
m / s 16, 46m / s
3,6
1
 Ek  .9,14.107.(16, 46)2  Ek  1, 24.1010 J
2
018
5.
Eop 
mf 
1
1
1 1
1
E0 f  m p v02 p  . m f v02 f  2m f v02 p  m f v02 f  4v02 f  v02 f
2
2
2 2
2
mp
2
1
1
E p  E f  m p (v0 p  1) 2  m f v02 f  2m f (v0 p  1) 2  m f v02 f
2
2
2
2
 2(v0 p  1)  v0 f  2(v0 p  1) 2  4v02 p  v02 p  2v0 p  1  2v02 p
 v02 p  2v0 p  1  0  v0 p  2,41m / s e v0 f  4,82 m / s
6.
d  (15m)iˆ  (12m) ˆj , F  (210 N )iˆ  (150 N ) ˆj
w  F .d  15.210  12.150  4950 J
7.
m  50kg , F  210 N
a)
b)
F
wF  F .d .cos  210.3.cos 20º  592 J
wP  P.d .cos90º  wP  0
120º
mg
c)
wh  h.d .cos90º  wh  0
d)
wtotal  wF  wP  wh  292 J
d
d=3 m
8.
m  3kg , x  3t  4t 2  t 3  v 
dx
 3  8t  3t 2
dt
p / ti  0  vi  3 m / s
p / t f  4s  v f  3  8.4  3.42  19 m / s
1
1
1
w  mv 2f  mvi2  .3(192  32 )
2
2
2
 w  528 J
9.
a.
d  (3m)iˆ, F1  5N ; F2  9N ; F3  3N
F
F
x
 F2 cos 60º  F1  9.cos 60º 5  0,5 N
y
 F2 sen60º  F3  9sen60º 3  4,79 N
 FR  (0,5 N )iˆ  (4,79 N ) ˆj
 w  FR .d  (3).(0,5)  0.479  w  1,5 J
b)
w  EkF  Eki , como w > 0
EkF > Eki
aumenta
y
F2
F1
60º
F3
x
019
10.
v0  0, F1  3N , F2  4 N , F3  10 N , d  4m
v0  0  FR
como
e
d tem a mesma direção e o mesmo sentido  w  FR .d
 F  F cos35º  F  F sen 50º
  F  10cos35º 3  4 sen50º  2,13N
 F  F sen35º  F cos50º  10 sen35º 4cos50º  3,16 N
x
3
1
2
x
y
3
y
F1
F3
35º
x
2
F2
FR  (2,13) 2  (3,16) 2  FR  3,81N
50º
w  3,81.4  w  15, 24 J
11.
m  20kg F  T
a) isolando a lata, temos que:
T
T
F
20.9,8
 Fy  0  T  T  mg  0  2T  mg  T  2
 F  98 N
mg
b) 4 cm
c)
wt'  ? T '  2T  2.9,8  196 N  wT '  T .d .cos0º  196.0,02  3,92 J
d)
wp  mg.d .cos180º  20.9,8.0,02  3,92 J
12.
a)
m  45kg , v  constante  a  0, sen 
x
 0  F  mg sen  0  F  45.9,8.sen 37º  F  265,4 N
b)
wF  F .d .cos180º  265,4.1,5  wF  398,1J
c)
wp  mg.d .cos53º  45.9,8.1,5.cos53º  wp  398,1J
d)
wn  n.d .cos90º  wn  0
e)
wtotal  w f  wP  wn  398,1  398,1  0
y
n
F
x
d
53º
1,5 m


mg
0,91 m
F
0,91
   37º
1,5
020
13.
m  72 kg , h  15 m, v0  0
a)
wT  ?,
T
(g/10)
a
cálculo de T
mg
g
1
 T  72.9,8(1  )  776,16 N
10
10
wT  T .h.cos  wT  776,16.15  wT  1, 2.10 4 J
F
y
 m.a  T  mg  m
b)
wp  mgh cos180º  72.9,8.15  wp  1,1.104 J
c)
wtotal  Ekf  Eki  wT  wP  Ekf  1,2.104  1,1.104  Ek f  Ekf  1000 J
d)
EkF 
1 2
1
mv f  1000  .72.v 2f  vF  5,3m / s
2
2
14.
v
v0  0
d
wT  T .d .cos180º  T .d
T
M
0
=0
a
(g/4)
mg
a)
F
y
 m.a  Mg  T  M
g
Mg 3Mg
3Mgd
 T  Mg 

 wT 
4
4
4
4
b)
wp  Mgd cos0º  wp  Mgd
c)
wtotal  Ek  wT  wP  Ekf  Eki 
d)
1
Mgd 1 2
Ekf  Mv 2f 
 Mv f  v f 
2
4
2
3Mgd
Mgd
 Mgd  Ekf  Ekf 
4
4
gd
2
C
15.
O trabalho é numericamente igual à área limitada pela força e o eixo x. Sendo que para área acima do
eixo x o trabalho é positivo e abaixo é negativo
 Tb  Ta  Tc  Td
021
16.
k  15 N / cm  1500 N / m
a)
xi  0, x f  7,6 mm  7,6.103 m
w
0
1
1
k ( xi2  x 2f )  .1500[(0  (7,6.103 ) 2 ]  w  4,3.102 J
2
2
b)
xi'  7,6.103 m, x 'f  15, 2.103 m
w' 
1
1
k ( x '2i  x '2f )  .1500[(7,6.103 )2  (15, 2.103 )2 ]  w'  0,13J
2
2
C
17.
m  250 g  0,25 kg , k  2,5 N / cm  250 N / m, d  12 cm  0,12m
a)
wp  mgd cos0º  0, 25.9,8.0,12  wp  0, 294 J
b)
w
1
1
k ( xi2  x 2f )  .250[0  (0,12) 2 ]  w  1,8 J
2
2
c)
wtotal  Ek  wp  w 
1 2 1 2
mv f  mvi
2
2
1
 0, 294  1,8   .0, 25.vi2  vi  3, 47 m / s
2
d)
vi'  2vi  2.3, 47  6,94 m / s
1
1
1
wtotal  Ek  mgd '  k ( yi2  y 2f )  mv 2f  mvi2
2
2
2
1
0,
25
 0, 25.9,8d  .250.d 2 
.(6,94) 2
2
2
2
 2, 45.d  125d  6,02  125d 2  2, 45d  6,02  0
Resolvendo esta equação do 2º grau teremos
d  0, 23 m
022
C
18.
m  2kg , Fx  6 x  k  6 N / m
a)
p / xi  3m  vi  8m / s
x f  4m, v f  ?
1
1
1
wFx  Ek  k ( xi2  x 2f )  mv 2f  mvi2
2
2
2
6 2
2
2
 (3  42 )  v 2f  .82  v f  6,56 m / s
2
2
2
b)
1
1
1
wFx  Ek  .6(32  x '2f )  .2.52  .2.82  x 'f  4,7m
2
2
2
C
19.
Área A1
m  5kg
10
(4  2).10

 30  n

2
 w  A1  A2  30  5  w  25 J
2.5

A2 
5

2
A1 
5
X (m)
4
2
-5
6
8
Área A2
C
C
20.
x
F  F0 (  1) 
x0
F
função do 1º grau
 o gráfico é um reta
F0
a)
A2
p / xi  0  Fi   F0 ,
A1
p / x f  2 x0  Ff  F0
n
w  A1  A2 , A1  A2  w  0
 F0
b)
xf
w   Fd x 
xi
 w  F0
2 x0

0
C
 x
2 x0
 F  x
0
0
0

 1 dx

2 x0
 x

 x2

 (2 x0 ) 2

 x   F0 
 2 x0   w  0
  1dx  F0 
 x0

 2 x0
0
 2 x0

x0
2x 0
x
023
21.
F  (2 xN )iˆ  (3N ) ˆj , ri (2m)iˆ  (3m) ˆj; rf  ( 4m)iˆ  (3m) ˆj
rf
xf
yf
4
3
xi
yi
2
3
w   F .dr   Fx dx   Fydy   2 xdx   3dx
'
ri
w
2x
2
2 4
3
 3x 3  42  22  3.(3)  3.3  6 J
2
C
22.
m  3.103 kg , h  210m, t  23s
w
Pm  T , a  0  T  mg
t
wT  T .h cos 0º  mgh  3.103.9,8.210  6,17.106 J
Pm 
T
v
constante
mg
6,17.106
 2,68.105 w
23
C
23.
m  100kg
v  5m / s  constante
F=122N
F
37º
v
P?
P  F .v  F .v.cos  122.5.cos37º  P  487,17 w
C
C
C
24.
u  25 J
x  7,5cm  7,5.102 m
1
1
u  kx 2  25  k .(7,5.102 )2  k  8,9.103 N / m
2
2
C
25.
m  2kg
a)
wg  mgh  2.9,8.8,5  166,6 J
b)
u  mgh f  mghi  mg (h f  hi )  2.9,8(1,5  10)  u  166,6 J
c)
ui  mghi  2.9,8.10  196 J
d)
u f  mgh f  2.9,8.1,5  29, 4 J
e)
wg  mgh  2.98.8,5  166,6 J
10 m
1,5 m
024
f)
u  mg (h f  hi )  2.9,8(1,5  10)  166,6 J
g)
u  u f  ui  196  100  ui  ui  296 J
h)
u  u f  ui  166,6  u f  296  u f  129,4 J
a)
hi  h f  T  0
b)
T  mgh / 2
c)
T  mgh
d)
uB  mg
e)
u A  mgh
C
C
26.
h
2
f) aumentaria
C
27.
a)
T  mgL cos0º  T  mgL
b)
T  mgL cos180º  T  mgL
c)
hi  h f  T  0
d)
u  mgL
e)
u  mgL
f)
hi  h f  u  0
h)
h 
é o mesmo
v=0
L
 u  é a mesma
C
28.
h  5R
P
a)
T  mgd cos0º  mg 4 R  4mgR
b)
T  mg 3R cos 0º  3mgR
c)
u p  mgh  mg 5R  5mgR
d)
uQ  mgR
e)
u  mg 2 R  2mgR
f)
T e u não dependem de v0 
h
R
todas permanecem as mesmas
Q
R
025
C
C
29.
a)
1
1
1
Ei  E f  mghi  mvi2  mgh f  mv 2f  ghi  v 2f 
2
2
2
v f  2 ghi  2.9,8.8,5  12,9 m / s
b) a mesma
c) aumentaria
C
30.
a)
1
1
1
Ei  E f  mghi  mvi2  mgh f  mv 2f  vi2  gL  vi  2 gL
2
2
2
b)
1
1
1
1
Ei  E f  mghi  mvi2  mgh f  mv 2f  gL  2 gL  v 2f  v f  2 gL
2
2
2
2
c)
1
1
Ei  E f  mghi  mvi2  mgh f  mv 2f
2
2
hi  h f  vi  v f  v f  2 gL
d) as velocidades não dependem da massa
 todas permaneceriam as mesmas
C
31.
a)
1
1
Ei  E A  mghi  mv02  mghA  mv A2 como hi  hA  v A  v0
2
2
b)
1
1
1
h 1
E A  EB  mghA  mvA2  mghB  mvB2  gh  v02  g  vB2  vB  gh  v02
2
2
2
2 2
c)
1
1
1
v2
EA  EC  mghA  mvA2  mghc  mvc2  gh  v02  c  vc  v02  2 gh
2
2
2
2
d)
1 2
1 2
1 2
2 gh  v02
EA  E f  mghA  mvA  mgh f  mv f  gh  v0  ghf  h f 
2
2
2
2g
e) as mesmas
C
32.
m  8 kg
 x  10cm  0,1m
a)
mg  k .x  k 
b)
u
mg 8.9,8

 784 N / m
x
0,1
1 2 1
kx  .784.(0, 4)2  62,72 J
2
2
026
c)
vi  v f  0  u (mola)  u (gravitacional)  u g  62,72 J
A energia potencial elástica é transformada em energia potencial gravitacional.
d)
ug  mghmax  mghi  62,72  8.9,8hmax  hmax  0,8m
C
33.
m  5 g  5.103 kg
V=0
x  8cm  8.102 m
a)
ug  mgh  5.103.9,8.20  0,98J
b)
vi  v f  0  Eki  E f  0  u g  s  us  0,98 J
20 m
V0=0
a energia potencial elástica é transformada em energia potencial gravitacional
c)
uso 
1 2
1
kx0  0,98  k .(8.102 )2  k  306, 25 N / m
2
2
C
34.
m  2 kg
k  19,6 N / cm  1960 N / m
x0  20cm  0,2m
h
1 2 1
kx1  .1960.(0, 2)2  39, 2 J
2
2
a)
u
b)
vi  v f  0  u( mola )  u( gravitacional )  u g  39, 2 J
c)
ug  mgh  39, 2  2.9,8h  h  2m
h
h
2
d 

 d  4m
d
sen 30º sen 30º
sen 30º 
C
35.
m  12 kg
x  2 cm  2.102 m  F  270 N
F  kx  270  k .2.102  k  13500 N / m
a)
uf 

1 2 1
kx  .13500.(5,5.102 )  20, 4 J , vi  v f  0
2
2
A energia potencial gravitacional é transformada em energia potencial da mola.
ui  u f  mgh  20, 42  12.9,8h  20, 42  h  0,174m
sen 30º=
b)
h
h
0,174
d 

 d  0,347m
d
sen 30º sen 30º
V0=0
027
1
ui  E f  mgh'  mv 2f  v f  2 gh' , d '  34,5  5,5  29 cm
2
'
h
sen 30º  '  h'  29.sen 30º  14,5 cm  0,145m  v f  2.9.8.0,145  v f  1,68 m / s
d
C
C
36.
Vi = 0
m  2kg , k  1960 N / m
Ei  E f
40 cm = 0,4 m
y
1
1
1
 mghi  mvi2  ky 2  mv 2f
2
2
2
1
 mg (0, 4  y )  .1960. y 2  19,6 y  7,84  980 y 2  y  0,099 cm
2
Vf = 0
C
37.
a) O valor da força é igual a inclinação da reta em cada intervalo
b)
Emax  U max  5J
c)
E  5J
d)
E  6J
e)
Ekmax  U min  FG
f)
 FAB  FCD  FBC  FDE  0
Vmin  Ekmax  U max  DE
C
38.
E  w fat
a)
h
1
1
1
 mgh f  mv 2f  (mghi  mvi2 )   c .mgD  gh  v02  c .gD
2
2
2
diminuir
D
diminui

b) D não depende da massa

menor
igual
D
h
C
39.
a)
EA  EB  u  diminui  Ek  aumenta
b)
EB  EC  u 
c)
u  é constante e v 
d)
AB
e
aumenta 
Ek 
diminui
BC  é constante
A
diminui
C
 Ek  diminui
B
D
028
CD 
diminui
C
40.
m  25kg , vi  0, h  12 m, v f  5,6 m / s
a)
u g  mgh f  mghi  25.9,8.12  2940 J
b)
Ek f 
1 2 1
mv f  .25.(5,6)2  392 J
2
2
c)
1
1
E  w fat  mgh f  mv 2f  (mghi  mv 2f )   Fat .h
2
2
 392  2940   Fat .12  Fat  212,33N
C
41.
m  30 g  3.102 kg x  12 cm  0,12m
vi  500 m / s
vf  0
a)
E  ? hi  h f  u  0
E 
b)
1 2 1 2
1
mv f  mvi   .3.102.5002  E  3750 J
2
2
2
E  wfat  3750   Fat .0,12  Fat  3,12.104 N
C
42.
m  2kg
 xo  15 cm  0,15 m
vi  v f  0  Eki  Ek f  0
k  200 N / m
d  75 cm  0,75 m
 ?
E  w fat  Ek f  u f  ( Eki  u f )   Fat .d
1
  k x02   c .mg .d
2
1
 .200(0,15) 2  c .2.9,8.0,75  c  0,153
2