MOVIMENTO HA 1. INTRODUÇÃO Um dos movimentos mais

Robinson F. Cadillo
Unir – Campus de Ji-Paraná
Ji
MOVIMENTO HARMÔNICO SIMPLES
(Versão 2014/2)
1.
INTRODUÇÃO
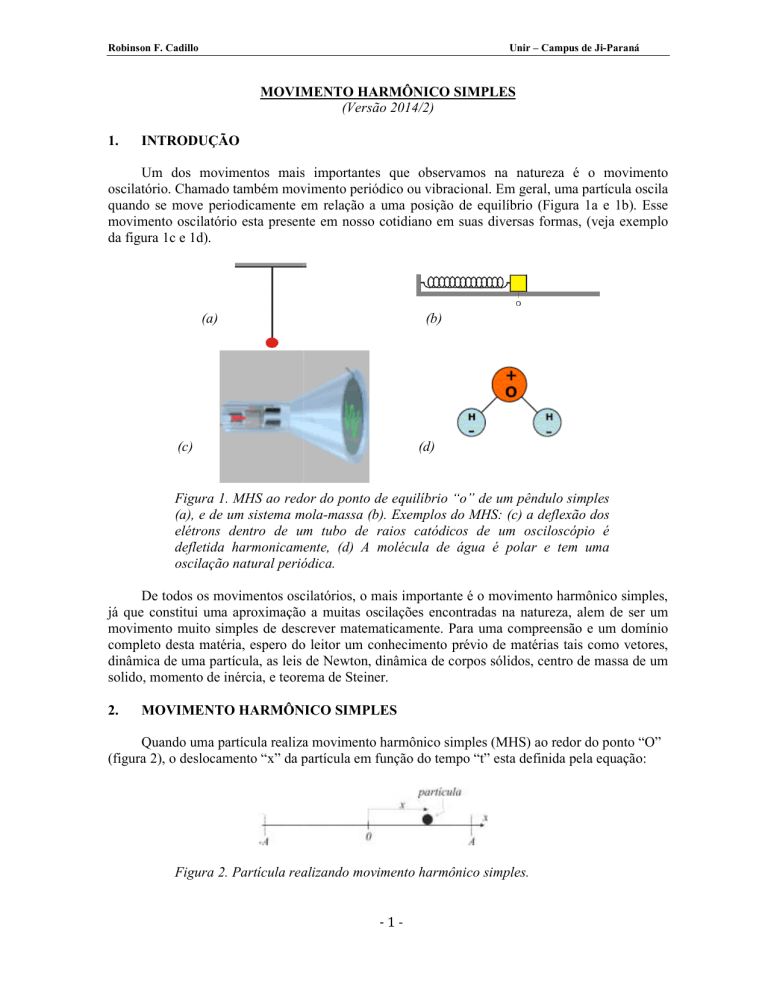
Um dos movimentos mais importantes que observamos na natureza é o movimento
oscilatório. Chamado também movimento periódico ou vibracional. Em geral, uma partícula oscila
quando se move periodicamente em relação a uma posição de equilíbrio (Figura 1a e 1b).
1b) Esse
movimento oscilatório esta presente em nosso cotidiano em suas diversas formas, (veja exemplo
da figura 1c e 1d).
(a)
(b)
(c)
(d)
Figura 1. MHS ao redor do ponto de equilíbrio “o” de um pêndulo
ndulo simples
(a), e de um sistema mola-massa
mola
(b). Exemplos do MHS: (c) a deflexão dos
elétrons dentro de um tubo de raios catódicos de um osciloscópio é
defletida harmonicamente, (d)) A molécula de água é polar e tem uma
oscilação natural periódica
periódica.
De todos os movimentos oscilatórios, o mais importante é o movimento harmônico simples,
já que constitui uma aproximação a muitas oscilações encontradas na natureza, alem de ser um
movimento muito simpless de descrever matematicamente. Para uma compreensão e um domínio
completo desta matéria, espero do leitor um conhecimento prévio de matérias tais como vetores,
v
dinâmica de uma partícula, as leis
eis de Newton, dinâmica de corpos sólidos, centro
entro de massa de um
solido, momento de inércia, e teorema de Steiner.
2.
MOVIMENTO HARMÔNICO SIMPLES
Quando uma partícula realiza movimento harmônico simples (MHS) ao redor do ponto “O”
(figura 2),, o deslocamento “x” da partícula em função do tempo “t” esta definida pela equação:
Figura 2. Partícula realizando movimento harmônico simples.
-1-
Robinson F. Cadillo
Unir – Campus de Ji-Paraná
= ∙ + (1)
Onde:
∙ + : fase, cuja unidade deve estar em rad.
: fase inicial (t = 0)
: Amplitude (deslocamento máximo a partir da origem)
: freqüência angular, onde [
]=rad/m
Observamos que x também pode se expressar de forma de cosseno e independente da função
usada, o movimento repete depois de um período T, de modo que ∙ = 2. Além disso, o
período T também esta relacionado com a freqüência de oscilação:
= ; onde = (2)
A velocidade da partícula fica determinada derivando o deslocamento x em relação do
tempo, veja equação 3. Observe, na equação, a velocidade máxima da partícula oscilante é ∙ .
=
= ∙ ∙ ∙ + (3)
Similarmente, a aceleração da partícula é obtida calculando a derivada da velocidade em
função do tempo. Isto é:
=
!
= − ∙ # ∙ ∙ + (4)
Observe desta ultima equação que ∙ # é a aceleração máxima da partícula. Alem disto,
observe no MHS, a aceleração é sempre proporcional e oposta ao deslocamento.
= −
# ∙ (5)
A figura 3 mostra as representações gráficas do deslocamento, velocidade e aceleração em
função do tempo t.
Problema resolvido
Uma partícula realiza MHS sobre o eixo x, segundo a equação:
xt = 1,0cm. cos.2π
π
rad
2 t + rad
2
s
(a) Calcule o deslocamento desse movimento em t = 3 s. (b) Calcule a velocidade da partícula em t
= 3 s. (c) Calcule a aceleração da partícula em t = 3 s. (d) Determine a fase do movimento em t =
3s. (e) Qual é a frequência desse movimento em t = 3s
Solução:
-2-
Robinson F. Cadillo
Unir – Campus de Ji-Paraná
Observe da equação a descrição do MHS da partícula: a amplitude = 1,0cm, a frequência
angular = 2π
345
6
e a fase inicial = rad.
x7s = 1,0cm. cos 892:
π
#
345
6
<
; 7s + rad= = 1,0> 9
#
7 = 1,0> ∙ .2:
7 = −
# ∙ 7 = − 92:
#
@; = −1,0>
rad
@
:
2 ∙ cos A.2:
2 7 + @B = 0
s
2
345 #
6
?<
; −1,0cm = C:# D
6E
A fase em 3s é obtida através do seguinte calculo:
rad
:
17:
A.2:
2 7s + radB =
@
s
2
2
345
Como = 2 = 2: , consequentemente:
6
= 1FG
Figura 3. Representação gráfica do movimento harmônico simples. (a)
deslocamento versus tempo, (b) velocidade versus tempo, e (c) aceleração
versus tempo. Repare que dado um tempo a velocidade esta fora de fase
com o deslocamento em 90º, e a aceleração esta fora de fase em 180º em
relação ao deslocamento.
-3-
Robinson F. Cadillo
3.
Unir – Campus de Ji-Paraná
DINÂMICA DE SISTEMAS OSCILANTES
Existem diferentes tipos de forças que dão origem a um MHS. Obviamente, essas forças
obedecem à segunda lei de Newton (H = > ∙ ), e estão relacionadas com a posição, segundo a
equação 5:
H = −
# ∙ > ∙ (6)
Observa-se a proporcionalidade entre a força e o deslocamento (equação 6), porém os
vetores estão dispostos em sentidos opostos. Definindo I = > ∙ # , como constante elástica, a
força no MHS será:
H = −I ∙ (7)
Por tanto, a força sempre aponta na origem “0”, veja figura 2, e é denotado como ponto de
equilíbrio dado que H = 0 (para o deslocamento x = 0). Podemos concluir também que F é uma
força atrativa, sendo o centro da atração o ponto “0”.
Considerando a constante elástica I , o período e a freqüência de oscilação da partícula
realizando MHS serão:
=
=
#J
= 2 ∙ L
∙L
K
#J
M
(8)
N
N
(9)
M
Por outra parte, fazendo uso da força elástica presente no MHS e desenvolvendo a segunda
lei de Newton
HO = −I ∙ O = > ∙
@# O
@ #
Nós temos a equação diferencial de segundo ordem:
Ou seja:
@# I
+ ∙ =0
@ # >
E
E
+∙ # = 0
(10)
Esta equação freqüentemente é chamada equação diferencial característica do MHS de
segundo ordem, cujo coeficiente do deslocamento define # . Em outras palavras, aplicando a
segunda lei de Newton em qualquer sistema físico que realiza MHS, conseguimos a equação
diferencial característica do MHS, e consequentemente a freqüência. A solução da equação 10 são
funções de ∙ . A seguir, veja as diferentes formas de soluções dessa equação:
= ∙ + (11)
= P
∙ + Q
(12)
-4-
Robinson F. Cadillo
Unir – Campus de Ji-Paraná
= R
∙ + S
∙ (13)
= T UK∙ + H VUK∙
(14)
Em cada uma das soluções equações 11-14, observamos um par de constantes de integração
e são calculados a partir das condições iniciais do MHS. Por exemplo, da solução 11, a amplitude
A e fase inicial são determinadas a partir das condições iniciais, tais como:
= 0 = W ;
= 0 = W
= 0 = W ;
= 0 =
ou;
W
= 0 =
= 0 = W ;
ou;
W
Nesta disciplina de Oscilações e Ondas utilizaremos as três primeiras soluções (equações
11-13) de todas as diferentes formas de solução citadas acima.
Problema resolvido:
Calcule as constantes Amplitude A e fase inicial da solução do MHS conhecendo as
condições iniciais W W .
Solução:
Partindo da solução da equação do MHS: = ∙ + , nós temos:
W = ∙ , e
W = ∙ ∙ Destas duas avaliações, calculamos a fase inicial e a amplitudes:
tan =
K∙Y
!Y
; e # =
KE ∙YE Z!YE
KE
Se a partícula se encontra na posição de equilíbrio iniciais W e logo depois recebe um impulso
com velocidade inicial W , a fase inicial será = 0, e a amplitude = W[
.
Exercício:
Calcule o par de constantes da solução 12, quando a condição inicial é:
= 0 = W ;
= 0 = W
(a)
= 0 = W
= 0 = W ;
(b)
= 0 = W
= 0 = W ;
(c)
Exercício
Calcule o par de constantes da solução 13, quando a condição inicial é:
(d)
= 0 = W ;
= 0 = W
= 0 = W
= 0 = W ;
(e)
= 0 = W
= 0 = W ;
(f)
-5-
Robinson F. Cadillo
Unir – Campus de Ji-Paraná
3.1.- Sistema Massa - mola
Em equilíbrio a mola não exerce força no objeto de
massa M. Quando objeto é deslocado de uma distancia x
a partir de sua posição de equilíbrio, a mola exerce uma
força –Kδ, onde δ é a deformação e K é a constante
elástica da mola. De acordo com a lei de Hooke:
Figura 4. O deslocamento x do objeto a
partir do ponto de equilíbrio é positivo se
a mola for estendida e negativa se a mola
for comprimida.
H = −I. \
Observe que a posição x da partícula coincide com a deformação da mola (\ = ). Por outra
parte, como estamos interessados em encontrar a equação característica de MHS para o sistema
massa-mola, aplicaremos a lei de Hooke na segunda lei de Newton do sistema:
H = −I. = ].
Portanto:
E E
+
N
^
. = 0
@# @ #
(15)
Conseguida a equação característica de MHS, identificamos a freqüência natural de
oscilação é # = I[].
3.2.- O pêndulo simples
O pêndulo simples é um tipo de oscilador harmônico constituído de um corpo cuja massa
“m” unido a um ponto fixo “o”, através de uma corda inextensível de comprimento “l”, veja figura
5. O MHS realizado pelo pendulo acontece em casos em que o ângulo _ é pequeno. Estudemos
agora o movimento deste sistema. Ou seja, nosso objetivo primário é calcular a freqüência depois
de encontrar a equação característica de MHS deste pêndulo.
Método 1: Fazendo uso da Segunda lei de Newton para forças tangenciais
A partícula se move segundo a trajetória de um arco de raio “l”. As forças que agem sobre
a partícula são o peso mg e a tensão T, ao longo da corda. Observamos da figura, a componente
tangencial da força Ft, que esta dado por:
H = −>` ∙ _
Onde o sinal menos se deve a que a força aponta em sentido contrario
ao deslocamento. A equação do movimento tangencial será:
H = −>` ∙ _ = > ∙
Com a aceleração tangencial esta relacionada com a
aceleração angular = a ∙b= a ∙
E c
E
, a equação de movimento
-6-
Figura 5. Pêndulo simples
de comprimento l, oscilando
ao redor do ponto fixo “o”.
Robinson F. Cadillo
Unir – Campus de Ji-Paraná
tangencial será:
@# _ `
+ _ = 0
@ # a
Considerando o ângulo _ pequeno, então a amplitude das oscilações também é pequena,
em conseqüência _d_ . Com isso a equação de movimento será:
E c
E
e
+ ∙_ =0
(16)
f
Método 2: Fazendo uso da Segunda lei de Newton para o movimento angular
Considerando Io o momento de inércia do pendulo, e sabendo o torque devido à tensão da
0 e devido ao peso da partícula é hO = >` ∙ a ∙ _−ijk , obtemos a equação de
corda é gO
movimento a partir da segunda lei de Newton para um movimento angular:
l ggO
hm =
gO
n
= ijk oW ∙
Ec
E
(17)
@# _
@ #
Onde ijk é o vetor unitário paralelo ao eixo de giro perpendicular ao plano descrito pelo pendulo e
que passa por “o”, cujo sentido é saindo desta folha.
Considerando novamente ângulos pequenos de _ , então _d_. Por tanto, temos o mesmo
resultado de equação de movimento do pendulo simples (equação 16), com frequência angular
`
= L [a.
−>` ∙ a ∙ _ = > ∙ a # ∙
O período de oscilação =
#J
K
f
= 2 ∙ L do pendulo não depende da massa m do corpo,
e
depende somente do comprimento l da corda e da aceleração da gravidade g.
3.3.- O pendulo físico
No pendulo físico articulado em “0” e com centro de
gravidade em G, figura 6. O torque devido ao peso mg é:
hk = −ijk ∙ > ∙ ` ∙ p ∙ _
gggO
Enquanto ao momento angular, tem-se:
gO
n
= ijk ∙ o ∙
E c
E
Novamente, sem perder o foco, nosso objetivo neste sistema é
calcular a freqüência angular de oscilação. Diante disso, a
partir da segunda lei de Newton do movimento angular (equação
13), e das duas relações anteriores nós temos:
@# _
−> ∙ ` ∙ p ∙ _ = o ∙ #
@
-7-
Figura 6. Pêndulo físico.
Robinson F. Cadillo
Unir – Campus de Ji-Paraná
Para deslocamentos angulares pequenos _d_, a equação anterior logra a forma seguinte:
E c
E
+
M∙e∙n
q
_=0
(18)
Novamente, nós estamos obtendo uma equação diferencial de segundo ordem, onde a partir da
freqüência angular (
# = >`pro ), tem-se o período de oscilação:
= 2 ∙ L
4.
q
(19)
M∙e∙n
ENERGIA NO MOVIMENTO HARMÔNICO SIMPLES
Fazendo uso da equação 3, a energia cinética Ec de uma partícula em MHS é:
1
1
∙ > ∙ # = ∙ > ∙ # ∙ # ∙ # + 2
2
1
Ts = ∙ > ∙ # ∙ # − # ∙ # + 2
Ts =
Ts = ∙ > ∙ # ∙ # − # #
(20)
Observação: a energia cinética máxima na posição = 0, e a energia cinética mínima na
posição = ±. Por outra parte, para obter a energia potencial lembremos a equação H =
uT
− v[u e da força envolvida (H = −I ∙ ) em partículas realizando MHS
uTv
=I∙
u
Integrando:
xy
w @Tv = I ∙ w ∙ @
z
z
Ou:
Tv = ∙ I ∙ # = ∙ > ∙ # ∙ #
#
#
(21)
Observação: a energia potencial é máxima em = ±, e mínima em = 0
Somando os resultados das equações 20 e 21 relacionadas à energia cinética (Ec) e à energia
potencial (Ep), tem-se:
Ts + Tv = ∙ > ∙ # ∙ #
#
-8-
(22)
Robinson F. Cadillo
Unir – Campus de Ji-Paraná
Observação: a energia total do oscilador harmônico é constante. Isto era esperado, já que a
força envolvida nesse tipo de movimento é conservativa.
A energia total do oscilador é uma constante de movimento alem das outras já conhecidas
como a aceleração da gravidade. Na figura 5, observa-se um intercambio freqüente entre a energia
cinética e potencial, segundo a posição do deslocamento. Alem disso, observa-se no gráfico Ep
versus x, a orientação da força elástica a partir da equação:
H=−
uTv
[ .
u
Figura 7. Representação gráfica da energia potencial e cinética de um oscilador
harmônico simples em função (a) do deslocamento, (b) e do tempo.
Movimentos oscilatórios próximos ao MHS
O movimento harmônico simples é um modelo para uma ampla variedade de fenômenos
físicos. Por exemplo, na estrutura de um sólido cujos átomos estão arranjados simetricamente.
Entre eles existe apresenta-se vibrações de um átomo em relação a outro. A energia potencial em
relação à distancia entre os átomos é mostrado na figura 6. O interessante do estudo do movimento
dos átomos que apresentam essas características é que elas podem se aproximar ao MHS,
próximos à posição de equilíbrio ro.
-9-
Robinson F. Cadillo
Unir – Campus de Ji-Paraná
Figura 8. Gráfico da energia potencial entre dois átomos de um sólido. Os
átomos movimentando-se próximos à posição de equilíbrio têm um
comportamento quase de MHS.
5.
Relação entre o MHS e o movimento circular
Existe relação entre o movimento circular uniforme e o MHS, a qual pode ser observada
fazendo uso do movimento circular uniforme de uma partícula, tal como é mostrado na figura 7. Si
consideramos que a partícula inicia seu movimento em t=0s, então o vetor posição da partícula
será:
{gO = ij ∙ { ∙ + ij| ∙ { ∙ Considerando agora a projeção da partícula sobre o eixo x:
O = ij ∙ { ∙ O aluno pode reparar que tal projeção esta realizando MHS. Alem disso, podemos ver o
radio que descreve a partícula vem ser o valor da amplitude A da projeção de tal partícula.
- 10 -
Robinson F. Cadillo
Unir – Campus de Ji-Paraná
Figura 9. A projeção do vetor R sobre o diâmetro, que
pousa no eixo x, descreve um movimento harmônico
simples.
- 11 -