modulo 1 eq da quantidade de mov

Módulo 1: Conteúdo programático – Equação da quantidade de
Movimento
Bibliografia: Bunetti, F. Mecânica dos Fluidos , São Paulo, Prentice Hall, 2007.
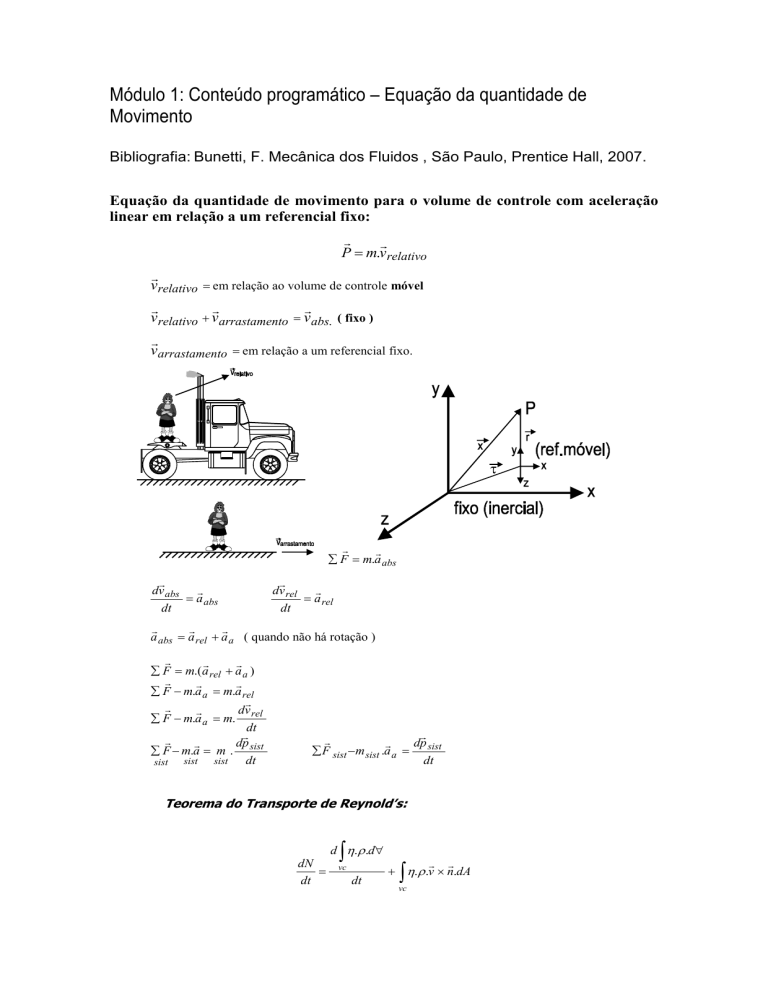
Equação da quantidade de movimento para o volume de controle com aceleração
linear em relação a um referencial fixo:
r
r
P = m.v relativo
r
vrelativo = em relação ao volume de controle móvel
r
r
r
vrelativo + varrastamento = v abs. ( fixo )
r
varrastamento = em relação a um referencial fixo.
r
r
∑ F = m.a abs
r
dv abs r
= a abs
dt
r
dv rel r
= a rel
dt
r
r
r
a abs = a rel + a a ( quando não há rotação )
r
r
r
∑ F = m.(a rel + a a )
r
r
r
∑ F − m.a a = m.a rel
r
r
dv rel
r
∑ F − m.a a = m.
dt
r
r
dp
r
∑ F − m.a = m . sist
dt
sist
sist
sist
r
r
dp
r
∑ F sist −m sist .a a = sist
dt
Teorema do Transporte de Reynold’s:
∫
d η.ρ .d∀
dN
=
dt
vc
dt
r r
+ η.ρ .v × n.dA
∫
vc
r
N=P
N
como η =
m
r
P r
então η = = v r
m
Logo resulta na eq da quantidade de movimento :
Projetando na direção “ x ” temos:
− ∫ ρ .d∀.aa =
ext.
x
vc
∑ Fx
d ∫ vr .ρ .d∀
r
r r
x
+ ∫ vr .ρ .v × n.dA
dt
s.c.
Projetando na direção “Y ” temos:
d ∫ vr .ρ .d∀
r
r r
y
∑ Fy
− ∫ ρ .d∀.aa =
+ ∫ vr .ρ .v × n.dA
ext.
dt
y
vc
s.c.
Projetando na direção “Z ” temos:
− ∫ ρ .d∀.aa =
ext
z
vc
∑ Fz
d ∫ vr .ρ .d∀
z
dt
r
r r
+ ∫ vr .ρ .v × n.dA
s.c.
1º EXERCÍCIOS RESOLVIDO
No esquema abaixo, o fluido água deixa o bocal com velocidade constante de 10 m/s, atingindo uma
placa plana. A área do bocal é de 100cm2. Determinar a força atuante aplicada pelo fluido à placa na
direção “ x ”. Considere regime permanente e propriedades uniformes nas superfícies de controle.
Adotar massa específica da água de 1000 kg/m3.
Da eq da quantidade de movimento para a direção X temos:
d ∫ vr .ρ .d∀
r
r r
x
∑ Fx − ∫ ρ .d∀.aa =
+ ∫ vr .ρ .v × n.dA
ext.
dt
x
vc
s.c.
A única força externa é a reação do placa no jato de fluido. Não há aceleração do volume de controle e o
regime é permanente logo:
r r r
− R = ∫ Vr ρVr xn dA
A
Na direção X só há uma fluxo de entrada no volume de controle e as propriedades são uniformes logo:
− R = −Vr ρVr ∫ dA = − ρVr A
2
A
Numericamente temos:
R = 1000.10 2.100.10 −4 = 1000 N
2º EXERCÍCIO RESOLVIDO
O tanque da figura, quando vazio, apresenta massa de 200 kg. A área da base do tanque é de 1m2. Os
atritos existentes podem ser desprezados. No interior do tanque, há uma coluna de fluido mantida
constantemente com 2m de altura. O fluido entra por 1 e sai por 2 e 3. Considerando o escoamento em
regime permanente e propriedades uniformes nas superfícies de controle, determinar:
a-)
b-)
A força aplicada ao cabo de aço;
A leitura da balança.
Dados: V1 = 10 m/s ; V2 = 5 m/s ; V3 = 17,5 m/s ; A1 = 20cm2 ; A2 = 5cm2 ; A3 = 10cm2 .
Da equação da quantidade de movimento para a direção X temos:
d ∫ vr .ρ .d∀
r
r r
x
∑ Fx − ∫ ρ .d∀.aa =
+ ∫ vr .ρ .v × n.dA
ext.
dt
x
vc
s.c.
A única força externa é a do cabo de aço aplicada ao tanque. Não há aceleração do volume de controle,
em X existem dois fluxos de saída e o regime é permanente logo:
− Rcabo
r r r
r r r
= ∫ Vr ρVr xn dA + ∫ Vr ρVr xn dA
A2
− Rcabo
A3
r
r
= + ∫ Vr ρVr dA + ∫ Vr ρVr dA
A2
A3
Projetando as velocidades no eixo X
− Rcabo = + ∫ Vr cos 60ρVr dA + ∫ − Vr ρVr dA
A2
A3
Como as propriedades são uniformes temos:
− Rcabo = + ρVr2 cos 60 ∫ dA − ρVr2 ∫ dA
A2
A3
Integrando
− Rcabo = + ρVr22 cos 60 A2 − ρVr23 A3
Pela equação da continuidade determina-se a velocidade 2
ρ1V1 A1 = ρ 2V2 A2 + ρ 3V3 A3
Como o fluido é incompressível
V1 A1 = V2 A2 + V3 A3
10.20 = V2 .5 + 17,5.10
V2 = 5
m
s
Substituindo os valores na Equação na quantidade de movimento temos:
V1 = 10 m/s ; V2 = 5 m/s ; V3 = 17,5 m/s ; A1 = 20cm2 ; A2 = 5cm2 ; A3 = 10cm2 .
− Rcabo = + ρVr22 cos 60 A2 − ρVr23 A3
Numericamente temos:
[
]
− Rcabo = 1000 5 2. cos 60.5 − 17,5 2.10 .10 −4 = −300 N
Rcabo = 300 N
Item B : Leitura da balança:
Este item consiste na aplicação da Equação da quantidade de movimento na direção Y
Nesta direção só há um fluxo de entrada, logo é negativo
r r r
RY − mg = ∫ Vr ρVr xn dA
A1
r
RY − mg = − ∫ Vr ρVr dA
A1
A projeção da velocidade é contra o eixo Y
RY − mg = − ∫ − Vr ρVr dA
A1
Como as propriedades são uniformes temos:
RY − mg = ρVr2 ∫ dA
A1
RY = ρVr21 A1 + mg
Numericamente temos:
R y = 1000.10 2.20.10 −4 + 200.10 = 2,2kN
1º EXERCÍCIO A SER RESOLVIDO PELO ALUNO
No esquema temos um canal de largura igual a 1,8m. Podemos considerar que nas
superfícies de controle 1 e 2, as velocidades são uniformes; na superfície 1 a velocidade
é de 0,5 m/s e há distribuição de pressão hidrostática. A comporta AB apresenta a
mesma largura do canal. Supondo regime permanente, determinar:
a-)
b-)
A velocidade na superfície de controle 2;
A força aplicada na comporta AB.
2º EXERCÍCIO A SER RESOLVIDO PELO ALUNO
No esquema, o carrinho com o jato de água, apresenta massa de 75 kg e está em repouso no instante t = 0
segundo. O carrinho é acelerado por um jato de água lançado por um bocal fixo, cuja área é 30cm2. A
velocidade do jato é de 35 m/s em relação ao bocal. Supondo não haver atritos e desprezando a resistência
do ar, determinar a velocidade do carrinho no instante t = 5 segundos. Considerar a variação da
quantidade de movimento do volume de controle desprezível e propriedades uniformes. Dados: A1 = A2
= 30cm2
3º EXERCÍCIO A SER RESOLVIDO PELO ALUNO
No esquema abaixo há escoamento em regime permanente com propriedades uniformes em todas as
seções de escoamento e o fluido é incompressível. Determinar :
a-)
b-)
c-)
O fluxo em massa pelo sistema de controle (1).
Sabendo-se que a superfície de controle (3) é circular, determinar o diâmetro.
A resultante das forças geradas pelos escoamentos
Dados: ρ = 1000 kg/m3 ; A1 = 20 cm2 ; A2 = 30 cm2 ; v1 = 2 m/s ; v2 = 2,5 m/s ; v3 = 1,5 m/s
4º EXERCÍCIO A SER RESOLVIDO PELO ALUNO
A turbina da figura extrai a potência de 2,9 kW da água do escoamento considerado
ideal. Calcular as forças exercidas sobre a redução e sobre a turbina respectivamente.
5º EXERCÍCIO A SER RESOLVIDO PELO ALUNO
Na instalação esquematizada, há o escoamento ideal de 314L/s de água (massa
específica de 1000 kg/m³) pelo interior da turbina. A pressão na entrada da mesma é
18N/cm² e na saída, vácuo com intensidade de 2 N/cm². Considerando a aceleração da
gravidade com intensidade de 10 m/s², determinar:
a) a potencia fornecida á turbina pelo escoamento de água
b) a força na direção X
6º EXERCÍCIO A SER RESOLVIDO PELO ALUNO
Um jato atinge uma pá que se localiza num plano inclinado. O peso do conjunto é 40N e
a área do jato 50 cm². Qual deve ser a velocidade do jato para que ocorra o equilíbrio
estático?