Espectro da luz

Introdução à Astrofísica
Lição 9 – O
Espectro da Luz
INTRODUÇÃO À ASTROFÍSICA
LIÇÃO 10 – O ESPECTRO
CONTÍNUO DA LUZ
A medição do brilho das estrelas está diretamente ligada à medida de
distância. A medida de distância é feita através da paralaxe, como já vimos.
Seja 𝑝 o Ângulo de paralaxe, a distância até o objeto, medido em parsec
(pc), será:
1
𝑑=
𝑝
O valor 1 representa a unidade astronômica.
O brilho de um objeto é medido em termos do fluxo recebido da fonte. O
fluxo é a quantidade total de energia em todos os comprimentos de onda
que atravessam uma área unitária do detector por unidade de tempo. Seja
um objeto de luminosidade L a uma distância r da Terra, e assumindo que
nenhuma luz é absorvida no caminho, o fluxo será:
𝐿
𝑓=
4𝜋𝑟 2
A magnitude é uma escala logarítmica do brilho de um objeto.
A magnitude absoluta é definida como a magnitude aparente que um objeto teria se fosse
colocado a uma distância de 10 pc. Uma diferença de 5 magnitudes corresponde a uma
diferença de 100 vezes o brilho. Assim:
𝑚1 −𝑚2
𝑓1
= 100 5
𝑓2
𝑓1
𝑚1 − 𝑚2 = −2,5 log
𝑓2
𝑚−𝑀
100 5
𝑑=
𝑓10
𝑑
=
=
𝑓
10𝑝𝑐
2
𝑚−𝑀+5
10 5 𝑝𝑐
𝑚 − 𝑀 = 5 log 𝑑 − 5
𝑚 − 𝑀 = 5 log
𝑑
10𝑝𝑐
Onde 𝑓10 é o fluxo que o objeto teria se estivesse a 10 pc, d é a distância e m-M é o módulo de
distância. Os “m” representam as magnitudes.
Exemplo: a magnitude aparente do sol é -26,83 e sua distância é 1 UA =
4,848 × 10−6 pc. Determine a magnitude absoluta e seu módulo de distância.
Fazemos:
𝑑
10−6
𝑀𝑆 = 𝑚 − 5 log
= −26,83 − 5 log 4,848 ×
= +4,74
10
10
𝑚 − 𝑀𝑆 = −31,57
Note que, quanto maior o brilho de um objeto, “menor” é sua magnitude.
Podemos analisar a temperatura de um corpo pela energia cinética média
dos seus átomos. Assim, um corpo absorvendo energia aumenta sua
temperatura. Os elétrons são acelerados e emitem radiação, o que reduz a
energia cinética dos átomos. Se a taxa de absorção é igual a taxa de
emissão, então o corpo está em equilíbrio térmico.
Um emissor ideal não reflete a luz, então o chamamos de corpo negro. A
radiação do corpo negro é o nome dado à essa emissão de energia. A
luminosidade L de um corpo negro de área A e temperatura T é dado por:
𝐿 = 𝐴𝜎𝑇 4
Onde 𝜎 = 5,6704 × 10−8 𝑊𝑚−2 𝐾 −4 é a constante de Stefan-Boltzmann.
Para uma estrela esférica de raio R com área 4𝜋𝑅²:
𝐿 = 4𝜋𝑅2 𝜎𝑇 4
O fluxo na superfície da estrela é:
𝑓𝑆 = 𝜎𝑇 4
Exemplo: a luminosidade do Sol é 𝐿⊙ = 3,839 × 1026 𝑊 e seu raio é 𝑅⊙ =
6,95508 × 108 𝑚. Temos então:
O fluxo na superfície é:
𝐿⊙
𝑇⊙ =
2
4𝜋𝑅⊙
𝜎
1
4
= 5777𝐾
4
𝑓𝑆 = 𝜎𝑇⊙
= 6,316 × 107 𝑊𝑚−2
A relação do comprimento de onda onde está a máxima emissão de
radiação eletromagnética de corpo negro com sua temperatura é dada
pela lei de Wien:
𝜆𝑚á𝑥 𝑇 = 0,0029 𝑚𝐾
Logo, para o Sol:
0,0029
𝜆𝑚á𝑥 ≈
= 501,6 𝑛𝑚
5777
Um dos grandes problemas para a física no final do século XIX, como vimos,
era derivar a curva representando a radiação de corpo negro.
Consideremos a função distribuição
espectral 𝑅(𝜆) para um corpo negro, que
determina a densidade de energia para
ondas eletromagnéticas no interior de
uma cavidade. Temos uma caixa com
uma cavidade, onde dentro existe
radiação. A probabilidade de um raio de
luz sair da cavidade antes de ser
absorvido pelas paredes internas é muito
pequena. A potência irradiada para fora
é proporcional à densidade total de
energia U no interior da cavidade. É
possível demonstrar que essa constante
de proporcionalidade é igual a c/4.
Então:
𝑐
4
Sendo 𝑢 𝜆 𝑑𝜆 a fração de energia por unidade de volume no interior da cavidade no
intervalo de comprimento de onda entre 𝜆 e 𝜆 + 𝑑𝜆, então:
𝑐
𝑅 𝜆 =𝑢 𝜆
4
Para calcular 𝑢(𝜆) basta determinar o número de modos de oscilações do campo
eletromagnético no interior da cavidade. Pode-se mostrar que o número de modos
de oscilação por unidade de volume, 𝑛(𝜆), não depende da forma da cavidade e é
dado por 𝑛 𝜆 = 8𝜋𝜆−4 .
De acordo com a teoria clássica, a energia média por modo de oscilação é igual a
𝑘𝑇, onde 𝑘 é a constante de Boltzmann. A distribuição espectral da densidade de
energia é:
𝑢 𝜆 = 𝑘𝑇𝑛 𝜆 = 8𝜋𝑘𝑇𝜆−4
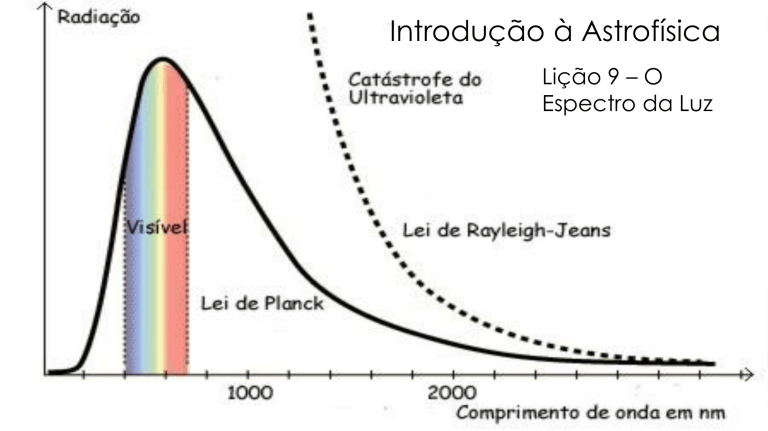
Essa é a lei de Rayleigh-Jeans. Para 𝜆 tendendo a zero, 𝑢(𝜆) tende a infinito. E isso é
um grave problema. Esse problema ficou conhecido como “catástrofe do
ultravioleta”.
𝑅 𝜆 =𝑈
Planck reformulou esse problema. Na época, se escrevia a função distribuição de energia como
𝑓 𝐸 = 𝐴𝑒 −𝐸/𝑘𝑇 , onde A é uma constante. Podemos escrever a energia média como:
∞
𝐸 =
𝐸𝑓 𝐸 𝑑𝐸
0
∞
𝐸𝐴𝑒 −𝐸/𝑘𝑇 𝑑𝐸
𝐸 =
0
𝐸 = 𝑘𝑇
Planck resolveu assumir que a energia não era contínua, mas sim discreta. Assim:
𝑛
𝐸𝑛 𝐴𝑒 −𝐸𝑛 /𝑘𝑇
𝐸 =
𝑖=0
𝜖
ℎ𝑐/𝜆
𝐸 = 𝜖/𝑘𝑇
=
=
𝑒
− 1 𝑒 ℎ𝜈/𝑘𝑇 − 1 𝑒 ℎ𝑐/𝜆𝑘𝑇 − 1
Multiplicando esse resultado pelo número de osciladores por unidade de volume entre 𝜆 e 𝜆 + 𝑑𝜆,
obtemos a função distribuição de densidade de energia no interior da cavidade:
E essa é a lei de Planck.
ℎ𝜈
8𝜋ℎ𝑐𝜆−5
𝑢 𝜆 = ℎ𝑐/𝜆𝑘𝑇
𝑒
−1
A densidade total de energia pode ser calculada integrando a nossa função:
∞
𝑈=
∞
𝑢 𝜆 𝑑𝜆 =
0
0
8𝜋ℎ𝑐𝜆−5
𝑑𝜆
ℎ𝑐/𝜆𝑘𝑇
𝑒
−1