Terceira Aula

Terceira Aula
Introdução à Astrofísica
Reinaldo R. de Carvalho ([email protected])
pdf das aulas estará em http://cosmobook.com.br/?page_id=440
Capítulo 3!
!
!
!
O Espectro Contínuo da Luz!
- Paralaxe estelar e Escala de Magnitude!
- A Natureza Ondulatória da Luz!
- A Quantização da energia!
- Índice de Cor!
Paralaxe Estelar
Medir o brilho intrínseco das estrelas está diretamente ligado à medida de
distância. Um dos métodos utilizados é a paralaxe trigonométrica.
Hipparcos Space Astrometry Mission (ESA) - 118.000 estrelas, precisão ~ 0.001ʺ, <
1kpc
Gaia Mission (ESA) - 1 bilhão de estrelas, precisão ~ 0.00001ʺ, nossa Galáxia e
outras próximas.
http://www.worldwidetelescope.org/
A Escala de Magnitude
➼ Desde a antiguidade que os astrônomos estabeleceram uma escala para
falar do “brilho” dos objetos. A magnitude aparente reflete somente como o
brilho do objeto “aparece” para um observador na Terra.
➼ No século XIX os astrônomos desenvolveram melhores formas de medir a
magnitude das estrelas e mostraram que uma estrela de “primeira magnitude”
era 100 vezes mais brilhante do que uma estrela de “sexta-magnitude”, ou seja
precisaria 100 estrelas de magnitude +6 para prover tanta luz quanto uma
estrela de magnitude +1.
➼ Para tornar os cálculos mais simples, os astrônomos re-definiram a escala
de magnitude tal que uma diferença de 5 corresponde exatamente a um fator
100 em brilho. Uma diferença de 1 magnitude, então corresponde a um fator
2.512 em brilho, porque
2.512 x 2.512 x 2.512 x 2.512 x 2.512 = (2.512)5 = 100
Fluxo e Luminosidade
O brilho de um objeto é medido em termos do fluxo recebido da fonte. O fluxo
é a quantidade total de energia em todos os comprimentos de onda que
atravessam uma área unitária do detector por unidade de tempo. O fluxo de
um objeto depende da luminosidade intrínseca do objeto (energia emitida por
segundo)
Seja um objeto de luminosidade
L a uma distância r da Terra.
Assumindo que nenhuma luz é
absorvida ao longo do percurso,
o fluxo é dado por:
Esta é a chamada lei do inverso do quadrado da distância. Exemplo: a luminosidade do Sol é L⊙ = 3.839 x 1026 W. A uma distância de
1UA = 1.496 x 1011 m a Terra recebe um fluxo (acima da atmosfera) do Sol
de:
Um observador a uma distância de 10 pc = 2.063 x 106 UA, mediria um fluxo
de 3.208 x 10-10 W m-2
Magnitude Absoluta
A magnitude absoluta é definida como a magnitude aparente que um objeto teria
se fosse colocado a uma distância de 10pc. Lembremos que uma diferença de 5 magnitudes corresponde a uma diferença de
100 vezes o brilho. Assim:
onde F10 é o fluxo que o objeto teria se estivesse a 10 pc, e d é a distância do objeto
em pc. A quantidade (m-M) é denominada módulo de distância.
Exemplo: a magnitude aparente do Sol é -26.83 e sua distância é 1UA = 4.848 x
10-6 pc. Determine a magnitude absoluta do Sol e o seu módulo de distância.
Para dois objetos à mesma distância temos que F2 / F1 = L2/L1 , o que vem
diretamente da lei do inverso do quadrado, F = L/4πr2. Para distâncias iguais,
da equação do módulo de distância temos que m1 - M1 = m2 - M2, assim:
Exercício: Mostre que a magnitude aparente de uma estrela, m, está
relacionada ao fluxo F pela expressão abaixo, onde FSun,10 é o fluxo recebido do
Sol a uma distância de 10pc.
O Experimento de Young
Grande parte da história da física se concentra na evolução de nossas idéias sobre a
natureza da luz.
Para Newton, a luz consistia de um conjunto de partículas enquanto que para Huygens a
luz poderia ser descrita pelas quantidades usuais que descrevem uma onda.
onde c = λν, λ é o comprimento de onda (figura) e ν a
freqüência, ou seja o numero de ondas por segundo que
passam num determinado ponto do espaço. Dada a
reputação de Newton, a luz foi preferencialmente
interpretada como onda, embora ambas propostas
explicassem os fenômenos de reflexão e refração.
Somente o experimento de dupla fenda de Young elucidou o problema, mostrando a
natureza ondulatória da luz.
Principio de superposição para a luz, criando interferência construtiva e destrutiva.
Um objeto opaco emite radiação eletromagnética de acordo com sua temperatura.
Radiação de Corpo Negro
A conexão entre a cor da luz emitida por um corpo quente e a sua temperatura foi feita
pela primeira vez por Thomas Wedgewood, um artesão de porcelana. Posteriormente,
investigações feitas por físicos mostraram que qualquer objeto com temperatura acima
do zero absoluto emite luz em todos os comprimentos de onda. A temperatura de um
corpo é determinada pela energia cinética média dos átomos, assim um corpo
absorvendo energia aumenta sua temperatura. Os elétrons são acelerados e emitem
radiação o que reduz a energia cinética dos átomos, diminuindo a temperatura. Se a
taxa de absorção é igual a taxa de emissão o corpo está em equilíbrio térmico com o
ambiente. A radiação eletromagnética emitida desta forma é denominada de radiação
térmica.
Como um emissor ideal não reflete luz, é
chamado corpo negro e a radiação que este
emissor re-emite é chamada radiação de corpo
negro. !
A figura mostram espectro de corpo negro a uma
temperatura T com o lixo em λmax. A relação
entre λmax e T é conhecida como Lei do
deslocamento de Wien, λmax T = 0.002897755 mK
Betelgeuse tem uma temperatura superficial de 3600 K logo λmax = 8.05 x 10-7 nm que
está na região infravermelho do espectro.
Rigel com uma temperatura superficial de 13000 K, tem λmax = 2.23 x 10-7 nm que está
na região ultravioleta do espectro.
A equação de Stefan-Boltzmann
Experimentos realizados por Josef Stefan mostraram que a luminosidade, L, de um
corpo negro de área A e temperatura T (em Kelvin) é dada pela expressão
Mais tarde Boltzmann demonstrou esta equação usando as leis da termodinâmica e a
expressão para a pressão de radiação obtida por Maxwell. A equação, agora
conhecida como Lei de Stefan-Boltzmann, tem um valor de σ = 5.6704 x 10-8 W m-2
K-4. Para uma estrela esférica de raio R, cuja área é A = 4 π R2 temos:
Como estrelas não são corpos negros perfeitos, definimos uma temperatura efetiva na
superfície da estrela. Combinando com a lei do inverso do quadrado temos que o
fluxo na superfície da estrela é dado por:
Exemplo: A luminosidade do Sol é L⊙ = 3.839 x 1026 W, e seu raio é R⊙ = 6.95508 x 108 m. A
temperatura efetiva pode então ser obtida como:
o fluxo na superfície solar é:
de acordo com a Lei de Wien, o espectro contínuo do Sol tem um máximo em
Este comprimento de onda cai na região “verde” do espectro eletromagnético. No entanto,
o Sol emite em toda a faixa de comprimento de onda e o olho humano percebe o Sol como
“amarelo”. O Sol emite grande parte de sua energia na região do visível e sendo a
atmosfera transparente a estes comprimentos de onda, o processo de seleção natural levou
o olho humano a ser mais sensível a este intervalo de comprimento de onda.
A quantização da energia
Um dos grandes problemas para os físicos do final do século XIX era derivar a curva
representando a radiação do corpo negro a partir de princípios físicos fundamentais.
Lord Rayleigh tentou chegar a uma expressão utilizando as equações de Maxwell junto
com as equações da termodinâmica. !
De maneira simplificada consideremos a função de distribuição espectral R(λ) para um
corpo negro, que determina a densidade de energia para ondas eletromagnéticas no
interior de uma cavidade.
!
A probabilidade de um raio sair da cavidade pelo furo antes de ser absorvido pelas
paredes internas é muito pequena. A potência irradiada para fora é proporcional à
densidade total de energia, U (energia por unidade de volume), no interior da cavidade. É
possível demonstrar que esta constante de proporcionalidade é igual a c/4. Assim, R(λ) =
Uc/4
Mas se u(λ)dλ é a fração de energia por unidade de volume no interior da cavidade no
intervalo de comprimento de onda entre λ e λ+dλ , então R(λ) = u(λ) c /4
Para calcular u(λ) basta determinar o numero de modos de oscilações do campo
eletromagnético no interior da cavidade, cujos comprimentos de onda estão no intervalo
λ e λ+dλ.
Pode-se mostrar que o número de modos de oscilação por unidade de volume, n(λ), não
depende da forma da cavidade e é dado por n(λ) = 8π λ-4. De acordo com a teoria clássica, a energia média por modo de oscilação é igual a kT onde
k é a constante de Boltzmann. Assim a distribuição espectral da densidade de energia é
dada por
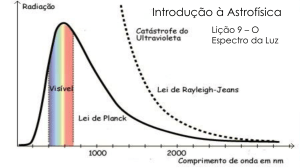
Esta expressão é conhecida como Lei de Rayleigh-Jeans.
Veja que para λ tendendo a zero u(λ) tende a infinito, em desacordo óbvio com os dados
experimentais. A enorme discrepância foi denominada “catástrofe do ultravioleta”.
Função de Planck para o corpo negro
Diante do problema da catástrofe do ultravioleta, Planck reformulou o problema de
determinação da distribuição de energia das partículas na cavidade. Na época,
classicamente se escrevia a função distribuição de energia como f(E) = Ae-E/kT, onde A é uma
constante e f(E) é a fração dos osciladores com energia entre E e E+dE. A energia média
pode ser escrita como:
Planck, ao invés de supor que a energia das cargas oscilantes era uma variável contínua
como está implícito na equação acima, era necessário assumir que a energia era discreta e
assumisse valores 0, ε, 2ε, 3ε … nε, onde n é um número inteiro. Além disso, ε deve ser
proporcional à freqüência, ou seja En = nhν, onde ν é a freqüência. Logo
Multiplicando este resultado pelo número de osciladores por unidade de
volume, entre λ e λ+dλ obtemos a função distribuição da densidade de energia
no interior da cavidade
Esta equação é denominada Lei de Planck e é representada na figura abaixo.
Para λ muito grande, usamos a aproximação ex ~ 1+x com x = hc/λKT. Assim
temos:
que é a fórmula de Rayleigh-Jeans.
Para valores muito pequenos de λ,
desprezamos o 1 no denominador e
temos
!
u(λ) ➝ 8πhcλ-5 e-hc/λKT ➝ 0
A Lei de Stefan-Boltzmann como !
conseqüência da Lei de Planck
A densidade total de energia pode ser calculada integrando a função
distribuição de densidade de energia para todos os comprimentos de onda.
Para calcular a integral, definimos uma variável adimensional x = hc/λKT e
neste caso dx = -hc dλ/λ2KT. Explicitando dλ temos dλ = -λ2(KT/hc)dx. Assim,
O valor da integral é π4/15 e nesse caso escrevemos U = (8π5 K4/15h3c3)T4 ➝ U = σT4.
A Função de Planck na Astrofísica
Consideremos em coordenas esféricas a quantidade de energia por unidade de
tempo tendo comprimento de onda entre λ e λ+dλ emitida por um corpo negro
de temperatura T e área dA que define um angulo sólido dΩ = senθdθdΦ.
As vezes é mais conveniente expressar em
termos de freqüência.
Assim, em coordenadas esféricas temos que a expressão acima para a
quantidade de energia escreve-se como:
A função de Planck pode ser usada para fazer a conexão entre propriedades
observadas (fluxo, magnitude aparente) e as correspondentes propriedades
intrínsecas (raio, temperatura)
Consideremos um modelo de estrela consistindo de um corpo negro esférico de
raio R e temperatura T. Vamos assumir que cada elemento de área dA emita
radiação de corpo negro isotropicamente. Assim, a energia por segundo tendo
comprimento de onda entre λ e λ+dλ que é emitida pela estrela será
A integração angular fornece um fator π e a integral sobre a área da esfera
fornece um termo 4 π R2. O resultado é então:
A quantidade Lλ dλ é denominada luminosidade monocromática. Da mesma
forma pode ser escrito o fluxo monocromático:
onde r é a distância à estrela. O termo Fλ dλ é o número de Joules de energia
da estrela com comprimento de onda entre λ e λ+dλ que chega por segundo em
um metro quadrado de um detector apontado para a estrela
Índice de Cor
O índice de cor é definido simplesmente como a razão de fluxos medidos em
duas regiões distintas do espectro eletromagnético.
g
r
O índice de cor é medido como a diferença entre a magnitude g e r, g-r, o que
representa uma razão de fluxos nas duas bandas passantes.
Exercícios
1 - Utilizando detetores fora da atmosfera terrestre, os astrônomos mediram o fluxo
médio de energia solar que chega à Terra (este valor é denominado constante solar), e
encontraram um valor de 1370 W m-2. Com esta informação calcule a temperatura na
superfície do Sol.
2 - A que distância devo colocar uma lâmpada de 100 W para que a mesma tenha um
fluxo radiante igual ao fluxo solar medido na superfície da Terra ? (utilize a constante
solar dada na questão 1
3 - Mostre que a magnitude aparente de uma estrela, m, está relacionada ao fluxo F pela
expressão abaixo, onde FSun,10 é o fluxo recebido do Sol a uma distância de 10pc.
4 - Uma estrela na constelação de Scorpius tem uma temperatura superficial de 28000
K, um raio R = 5.16 x 109 m e se encontra a uma distância de 123 pc. Calcule a) sua
luminosidade em unidades da luminosidade solar; b) sua magnitude absoluta, sabendo
que a magnitude absoluta do Sol é 4.74; c) seu módulo de distancia sabendo que sua
magnitude aparente é de -1.02; d) o fluxo na superfície da estrela; e) o fluxo na
superfície da Terra (compare com a constante solar); e f) o comprimento de onda
máximo da radiação recebida.