Experiência de Millikan (1909

Espectrómetro
Espectrómetro de
de Massa
Massa
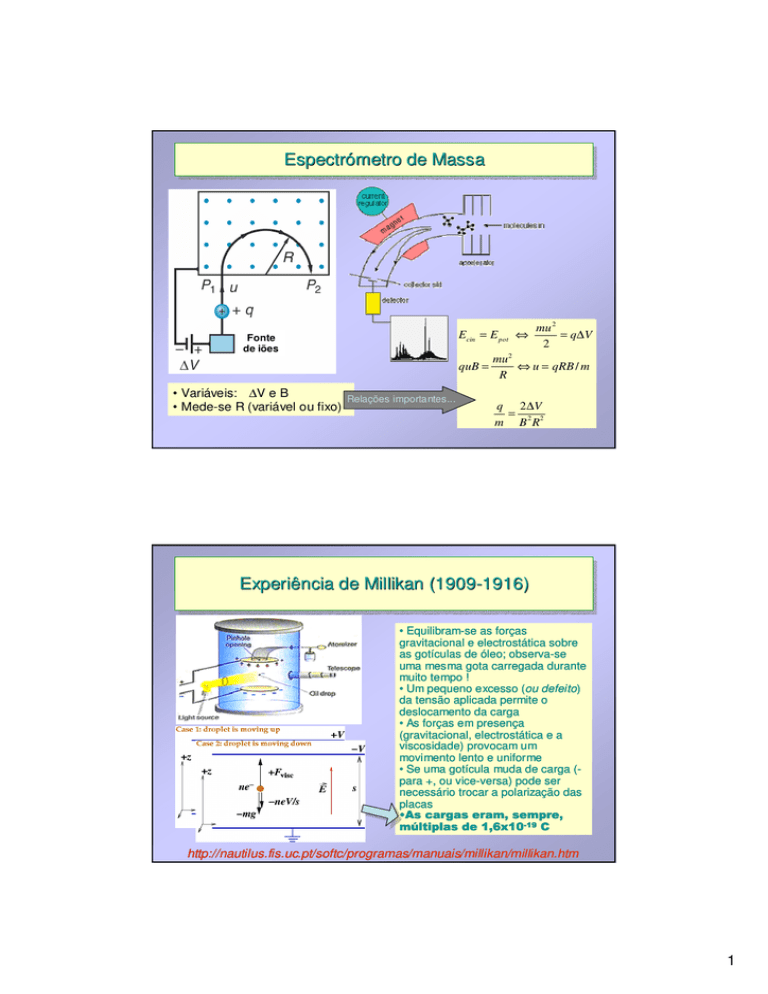
Ecin = E pot ⇔
Fonte
de iões
quB =
• Variáveis: ∆V e B
• Mede-se R (variável ou fixo)
Relações importantes...
mu 2
= q ∆V
2
mu2
⇔ u = qRB / m
R
q 2 ∆V
=
m B 2 R2
Experiência
-1916)
(1909
Experiência de
de Millikan
Millikan (1909(1909-1916)
• Equilibram
Equilibram--se as forças
gravitacional e electrostática sobre
as gotículas de óleo; observaobserva-se
uma mesma gota carregada durante
muito tempo !
• Um pequeno excesso (ou
(ou defeito)
defeito)
da tensão aplicada permite o
deslocamento da carga
• As forças em presença
(gravitacional
gravitacional,, electrostática e a
viscosidade) provocam um
movimento lento e uniforme
• Se uma gotícula muda de carga ((para +, ou vicevice-versa) pode ser
necessário trocar a polarização das
placas
http://nautilus.fis.uc.pt/softc/programas/manuais/millikan/millikan.htm
http://nautilus.fis.uc.pt/softc/programas/manuais/millikan/milli
kan.htm
1
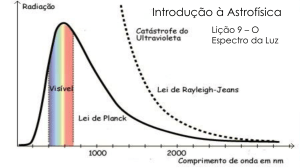
Diversos espectros de corpo negro
(a) Rho Ophiuchi
Ophiuchi,, uma nebulosa gasosa
fria e invisível. À temperatura de 60
K, emite essencialmente ondas de
rádio de baixa frequência.
(b) Uma estrela jovem e pouco brilhante
(a vermelho) perto do centro da
nebulosa de Orion. A atmosfera da
estrela, a 600 K,
K, emite sobretudo no
infra--vermelho
infra
vermelho..
(c) A superfície do Sol, a cerca de 6000
K, tem o maior brilho na zona visível
do espectro electromagnético.
(d) Omega Centauri
Centauri,, um agrupamento
de estrelas muito brilhantes,
observada por um telescópio do
“ space shuttle
shuttle”.
”. A uma temperatura
de 60,000 K,
K, estas estrelas radiam
intensamente no ultra
ultra--violeta
violeta..
Radiação
Radiação ee Temperatura
Temperatura
Spectrum of the Cosmic Microwave
Background Radiation as measured by
the FIRAS instrument on COBE and a
black body curve for T = 2.7277 K. The
error flags have been enlarged by a
factor of 400. Any distortions from the
Planck curve are less than 0.005% (see
Fixsen et al. 1996).
Máximo da Emissão
versus
Temperatura
2
Radiação
Radiação do
do Corpo
Corpo Negro
Negro
Absorção
Absorção==Emissão
Emissão
• J.Stefan (1879)
(1879)--L.Boltzmann (1884)
POTÊNCIA TOTAL EMITIDA/m2
R = σ T4
σ = 5,6703x10-8 W/m2K4
• Wien
λ maxT = Const = 2,898x10-3 mK
Plank
Plank ee aa Radiação
Radiação do
do Corpo
Corpo Negro
Negro
Lei de RAYLEIGHRAYLEIGH-JEANS
u ( λ ) = kTn ( λ ) = 8 π kT λ
Lei
Lei de
de PLANK
PLANK (1900)
(1900)
−4
u(λ) = densidade de energia das oscilações
para os n(λ) modos da cavidade
• OK para λ longo...
• Mas ... “CATÁSTROFE do ultra-violeta” !
∞
u (λ )d λ → ∞
u (λ ) =
8πhc
hc
λ5 (e λkT − 1)
-34 Js)
hh == 6.626
6.626 xx 10
10-34
Js) λλ == comprimento
comprimento de
de
onda
onda (m)
(m)
onst de
-23 J/K
kk == C
Const
de Boltzmann
Boltzmann == 1.38
1.38 xx 10
10-23
J/K
TT == Temperatura
Temperatura (K)
(K)
0
hh determinável
determinável
aa partir
partir do
do
ajuste
ajuste da
da lei
lei de
de
Planck
Planck ao
ao
espectro
espectro de
de
radiação
radiação do
do
corpo
corpo negro
negro !!
3