3a-serie-revisao - MASCENA CORDEIRO

Exercícios de revisão de Geometria Plana – Prof. Mascena Cordeiro
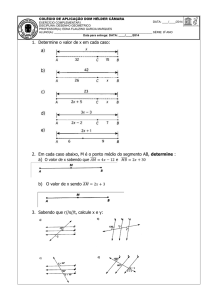
01) (IFBA) Na figura abaixo, sendo r // s // t, o valor de x é:
02) Observe a figura r // s // t. Calcule o valor de x de acordo com o Teorema de Tales.
03) Três terrenos têm frente para a rua A e para a rua B, como na figura. As divisas laterais são perpendiculares à rua A.
Qual a medida de frente para a rua B de cada lote, sabendo que a frente total para essa rua tem 180 m?
04) No triângulo ABC a seguir, o segmento DE é paralelo ao segmento BC. Determine o valor de x aplicando a
proporcionalidade entre segmentos paralelos cortados por segmentos transversais.
05) A piscina de um clube tem 1,80m de profundidade, 14m de largura e 20m de comprimento. Calcule quantos litros de
água são necessários para enchê-la.
a)
b)
c)
d)
e)
504 000
340 000
250 000
300 000
450 000
06) ( UFSC ) O volume de um paralelepípedo retângulo é 24 m3. Sabendo-se que suas dimensões são proporcionais aos
números 4, 3 e 2, calcule, em metros quadrados, a área total desse paralelepípedo .
07) ( UFRGS – 08 ) O custo de uma embalagem é diretamente proporcional à superfície do sólido que se deseja embalar.
Se o custo para embalar um cubo de 40 cm de aresta é R$ 10,00, a embalagem de um cubo de 80 cm de aresta custa,
em reais,
a. 15
b.
c.
d.
e.
20
25
40
80
08) Considere um pedaço de cartolina retangular de lado menor 10 cm e lado maior 20 cm. Retirando-se 4 quadrados iguais
de lados x cm (um quadrado de cada canto) e dobrando-se na linha pontilhada conforme mostra a figura, obtém-se uma
pequena caixa retangular sem tampa. O polinômio na variável x, que representa o volume, em cm3, desta caixa é
a)
b)
c)
d)
e)
4x3 – 60x2 + 200x
4x2 – 60x + 200
4x3 – 60x2 + 200
x3 – 30x2 + 200x
x3 – 15x2 + 50x
09) ( PUC-SP ) Qual é o polígono regular em que o número de diagonais é o dobro do número de lados?
a)
b)
c)
d)
e)
Dodecágono
Pentágono
Octógono
Heptágono
Hexágono
10) (FAAP-SP 97) A medida mais próxima de cada ângulo externo do heptágono regular da moeda de R$ 0,25 é:
a)
b)
c)
d)
e)
60°
45°
36°
83°
51°
11) (USP) No quadrilátero ao lado, BC = CD = 3 cm, AB = 2 cm, e. A medida, em cm, do perímetro do quadrilátero é:
a) 11
b) 12
c) 13
d) 14
e) 15
12) (USP) No quadrilátero ABCD ao lado, ABC = 150º, AD = AB = 4 cm, BC = 10 cm, MN = 2 cm, sendo M e N,
respectivamente, os pontos médios de CD e BC. A medida, em cm2, da área do triângulo BCD é :
a) 10
b) 15
c) 20
d) 30
e) 40
13) (USP) Dois dos ângulos internos de um polígono regular medem 130° cada um e os outros ângulos medem 128° cada,
o número de lados do polígono é:
a) 5
b) 6
c) 7
d) 8
e) 9
14) (USP) No retângulo abaixo, o valor, em graus, de a + b é:
a) 50
b) 90
c) 120
d) 130
e) 220
15) ( MACK-SP ) Os ângulos externos de um polígono regular medem 20°. Nessas condições calcule o número de diagonais
desse polígono.
16) ( PUC -PR ) Quanto mede a soma dos ângulos internos de um hexágono regular?
17) (Mackenzie - SP) Os ângulos externos de um polígono regular medem 20°. Então, o número de diagonais desse
polígono é:
a) 90
b)104
c)119
d)135
e)152
18) Os números dos lados de dois polígonos convexos são consecutivos e um deles tem 9 diagonais a mais que o outro.
Que polígonos são esses?
19) A medida de cada ângulo externo de um polígono regular é 1/4 da medida de um ângulo interno. Quantas diagonais
tem o polígono?
20) (Puc-Rio) Os ângulos internos de um quadrilátero medem 3x - 45, 2x + 10, 2x + 15 e x + 20 graus. O menor ângulo
mede:
a) 90°
b) 65°
c) 45°
d) 105°
e) 80° R: b