Capítulo 2: Programação Linear

Capı́tulo 2
Programação Linear
2.1
Introdução
Modelos lineares de otimização aos quais eventualmente se incorporam restrições de integralidade das variáveis de decisão são os mais utilizados em planejamento. Quando do surgimento do método Simplex para Programação Linear,
argumentava-se que modelos lineares não seriam adequados para representar problemas reais, uma vez que quase todos os problemas de interesse possuiam caracterı́sticas não–lineares. Entretanto, o método Simplex tornou possı́vel resolver
problemas relativamente grandes (em termos de número de variáveis e restrições),
o que nenhum outro método era capaz à época. Uma melhor compreensão das potencialidades e limitações da modelagem linear levou a inúmeras aplicações práticas
do método.
Rapidamente constatou-se que a aplicabilidade da modelagem linear poderia
ser substancialmente espandida se fosse possı́vel tratar problemas com variáveis de
decisão restritas a valores inteiros ou binários (0 ou 1), o que permitiria incorporar à
modelagem de problemas de planejamento um tipo importante de não–linearidade.
Desenvolvimentos nesta linha deram origem às Programações Inteira, Inteira/Mista
e Combinatória, cujos métodos podem ser vistos como extensões dos métodos da
Programação Linear.
A modelagem linear e a solução de problemas de produção por meio do método
Simplex são os principais objetivos deste capı́tulo. Por conveniência, modelos com
variáveis de decisão inteiras ou binárias são também considerados; métodos adequados para tratar estes modelos serão discutidos a partir do Capı́tulo 3.
2.2
Hipóteses básicas
Uma empresa pode ser vista como um sistema que transforma recursos em
produtos por meio de métodos ou tecnologias adequadas. Tipicamente os recursos
consistem de matérias–primas, força de trabalho (homens/hora), disponibilidade de
equipamentos e bens intermediários, adquiridos de outras empresas. Os produtos
9
10
Capı́tulo 2. Programação Linear
podem ser bens ou serviços acabados para consumo, ou intermediários, a serem
comercializados com outras empresas.
Certas hipóteses são necessárias para que modelos lineares representem adequadamente problemas de produção.
Proporcionalidade
Modelos lineares adotam a hipótese de que se o custo de produção de uma
unidade (custo unitário) de um produto j é cj , então xj unidades do produto custam cj xj . Se pj é o preço unitário de venda do produto j, então xj unidades do
produto são vendidas por pj xj . Na modelagem linear, se a produção de uma unidade do produto j consome aij unidades do recurso i, então xj unidades do produto
consomem aij xj do recurso i.
A hipótese de proporcionalidade pode deixar de corresponder à realidade.
Exemplo: o custo (preço) unitário de produção (venda) pode decrescer a partir de
um significativo aumento da quantidade produzida (vendida).
Aditividade
Pela hipótese da aditividade, se os custos unitários de produção de dois produtos, j e k, são cj e ck , respectivamente, então o custo total para produzir xj e
xk unidades dos produtos é cj xj + ck xk , o mesmo aplicando-se ao valor total de
venda de produtos. Se a produção de uma unidade do produto j e de uma unidade
do produto k consomem aij e aik unidades do recurso i, respectivamente, então o
consumo total do recurso i é aij xj + aik xk .
A hipótese de aditividade implica que produtos podem ser produzidos independentemente. Pode deixar de ser válida se houver interação entre produções.
Exemplo: dois produtos utilizam um mesmo recurso com diferentes eficiências
Divisibilidade
Significa que as variáveis de decisão podem assumir qualquer valor real, isto
é, valores fracionários (não–inteiros) representam decisões viáveis.
A hipótese de divisibilidade pode ser adotada quando as variáveis de decisão
significam, por exemplo, quanto produzir de cada produto, e produtos não–acabados
durante um perı́odo de produção (dia, semana, mês, ano, etc.) podem ser acabados
no perı́odo seguinte. Entretanto, se significarem quantidades de produtos para
entregas em datas pré–determinadas, variáveis de decisão assumindo apenas valores
inteiros podem ser necessárias.
Existem ainda situações nas quais deve-se selecionar que produtos produzir
dentro de uma lista de produtos possı́veis. Para indicar seleção ou atribuição, usa-se
geralmente variáveis de decisão binárias: valores iguais a 1 indicam que os custos
de produção e recursos utilizados pelos produtos assim selecionados devem ser con-
2.3. Modelos lineares
11
tabilizados; valores iguais a 0 indicam exatamente o contrário.
Determinismo
Os parâmetros presentes no modelo – custos, preços unitários, recursos –
são precisamente conhecidos. Assume-se que eventuais incertezas quanto a estes
parâmetros foram eliminadas e que dispõe-se de um modelo determinı́stico equivalente.
A hipótese de determinismo costuma ser afetada pelo perı́odo de planejamento.
Em perı́odos longos, as previsões de demandas e recursos tornam-se mais imprecisas,
dificultando a determinação de custos de produção e preços de venda de produtos.
2.3
Modelos lineares
As hipóteses de proporcionalidade e aditividade levam a modelos de otimização integralmente representados por funções lineares. Uma função z = z(x) é
linear nas variáveis de decisão x1 , x2 , . . . , xn quando existem coeficientes α1 , α2 ,
. . . , αn tais que
z(x) = α1 x1 + α2 x2 + · · · + αn xn .
Supondo que x1 , x2 , . . . , xn são as quantidades produzidas de n produtos e
c1 , c2 , . . . , cn são os custos unitários de produção associados, então o custo total
de uma empresa pode ser expresso por meio da função linear
zc (x) = c1 x1 + c2 x2 + · · · + cn xn .
A rigor, zc (x) é o custo total variável (com as quantidades produzidas) da
empresa. Geralmente existe uma segunda parcela de custo, chamada de custo total
fixo, incorrido pela empresa independentemente das quantidades produzidas, que
deve ser somado a zc para se obter o custo total de produção. Entretando, a
existência de custos fixos não gera dificuldades para a solução de problemas de
programação linear.
De forma análoga, a receita total e o lucro total da empresa são expressos
pelas funções lineares
zr (x) = p1 x1 + p2 x2 + · · · + pn xn
e
zl (x) = zr (x) − zc (x),
respectivamente. As funções zc , zr e zl são exemplos de funções–objetivos para
problemas de produção modelados por meio da abordagem linear.
As hipóteses de proporcionalidade e aditividade permitem que as restrições do
problema sejam representadas por equações e/ou inequações lineares nas variáveis
de decisão. Especificamente, se aij denota a quantidade de um recurso i utilizado
12
Capı́tulo 2. Programação Linear
para produzir uma unidade do produto j, e bi é a quantidade total disponı́vel do
recurso, então a escolha das quantidades a produzir deve respeitar a desigualdade
ai1 x1 + ai2 x2 + · · · + ain xn ≤ bi .
Deve haver uma desigualdade deste tipo para cada tipo de recurso utilizado.
Se bi , i = 1, 2, . . . , m denotarem as quantidades totais de m recursos disponı́veis
e o objetivo do problema for maximizar a receita total decorrente da produção da
empresa, então o problema de otimização linear correspondente será dado por
maximizar z = c1 x1 +
c 2 x2 + · · · +
c n xn
sujeito a
a
x
+
a
x
+
·
·
·
+
a
≤ b1 ,
11
1
12
2
1n xn
a
x
+
a
x
+
·
·
·
+
a
x
≤ b2 ,
21
1
22
2
2n
n
(2.1)
..
..
..
..
.
.
.
.
am1 x1 + am2 x2 + · · · + amn xn ≤ bm ,
x1 ≥ 0,
x2 ≥ 0,
...,
xn ≥ 0.
No problema (2.1) adota-se a hipótese da divisibilidade: as variáveis de decisão
são quaisquer reais não–negativos. Formulações similares, mas envolvendo diferentes
interpretações para variáveis de decisão e restrições a serem satisfeitas são muito
freqüentes em programação linear.
Exemplo 2.1 (Problema da dieta) O chamado problema da dieta foi o primeiro
problema linear formulado e resolvido com o uso de métodos de programação linear.
Assume-se que estejam disponı́veis n diferentes alimentos (carne, leite, ovos, suco
de laranja, . . . ) e que o custo unitário do i-ésimo alimento é ci , i = 1, 2, . . . , n. A
dieta deve atender a exigências diárias mı́nimas de m diferentes nutrientes (vitaminas, proteı́nas, carboidratos, . . . ). Os nı́veis mı́nimos de nutrientes são representados por bj , j = 1, 2, . . . , m; supõe-se que cada alimento i possui aij unidades do
nutriente j por unidade do alimento i. Se as quantidades totais (não-negativas) dos
n alimentos forem representadas por x1 , x2 , . . . , xn , o problema da dieta assume a
forma
minimizar
c 1 x1 +
c 2 x2 + · · · +
c n xn
sujeito a
a
x
+
a
x
+
·
·
·
+
a
≥ b1 ,
11
1
12
2
1n xn
a
x
+
a
x
+
·
·
·
+
a
x
≥ b2 ,
21
1
22
2
2n
n
..
..
..
..
.
.
.
.
a
x
+
a
x
+
·
·
·
+
a
x
≥
bm ,
m1 1
m2 2
mn n
x1 ≥ 0,
x2 ≥ 0,
...,
xn ≥ 0.
A formulação do problema da dieta pode ser refinada de várias maneiras. É
possı́vel, por exemplo, que a solução de mı́nimo custo seja tal que poucos alimentos
(apenas os mais baratos) façam parte da dieta diária. Uma forma de evitar a
saturação do indivı́duo com uma dieta muito simples é incorporar restrições com
valores máximos para as quantidades de alimentos, isto é, incorporar restrições de
desigualdade do tipo xi ≤ x̄i , i = 1, 2, . . . , n. A nova dieta será, provavelmente,
mais diversificada, embora também mais cara do que a original.
2.4. Forma padrão
13
Uma hipótese mais realista seria imaginar que as quantidades dos alimentos
devem ser determinadas na forma de porções (porções de carne, porções de arroz,
. . . ), ao invés de quantidades arbitrárias de alimentos. (As primeiras aplicações do
problema da dieta visavam oferecer uma dieta diária de baixo custo para o Exército
Americano e a dieta deveria ser servida em porções.) Se levarmos em conta esta
hipótese, o problema passa a envolver variáveis de decisão inteiras não-negativas. 2
2.4
Forma padrão
Para modelos de programação linear é possı́vel estabelecer uma formulação
matemática geral conhecida como forma padrão: qualquer problema de programação linear pode ser convenientemente manipulado e colocado nesta forma. A
partir de uma forma padrão torna-se mais fácil desenvolver e implementar métodos
como o Simplex, a ser discutido neste capı́tulo. A forma padrão de um problema
de programação linear é a seguinte:
minimizar z = c1 x1
sujeito a
a11 x1
a21 x1
am1 x1
x1 ≥ 0,
+
+
+
..
.
c 2 x2
a12 x2
a22 x2
+
+
+
..
.
···
···
···
+
+
+
..
.
c n xn
a1n xn
a2n xn
+
am2 x2
x2 ≥ 0,
+
···
...,
+
amn xn
xn ≥ 0.
=
=
..
.
b1 ,
b2 ,
=
bm ,
(2.2)
As constantes ci , bj e aij , i = 1, 2, . . . , n, j = 1, 2, . . . , m caracterizam um
problema particular de programação linear. Um problema na forma padrão (2.2)
possui n variáveis de decisão, m restrições de igualdade e a função–objetivo deve
ser minimizada. Assume-se ainda que bj ≥ 0 para j = 1, 2, . . . , m
Procedimentos simples podem ser adotados para se chegar à forma padrão de
um problema de programação linear qualquer.
Variáveis de excesso
Suponha que o problema linear original apresenta uma restrição de desigualdade do tipo
aj1 x1 + aj2 x2 + · · · + ajn xn ≥ bj .
A restrição de desigualdade pode ser substituı́da por uma restrição de igualdade introduzindo-se uma variável adicional xn+1 , não-negativa, conhecida como
variável de excesso:
aj1 x1 + aj2 x2 + · · · + ajn xn − xn+1 = bj .
Introduz-se tantas variáveis de excesso quantas forem as restrições do tipo
”≥” presentes no modelo original. Um novo conjunto de variáveis será formado
pelas variáveis de decisão originais mais as variáveis de excesso.
14
Capı́tulo 2. Programação Linear
Variáveis de folga
Suponha agora que o problema linear original apresenta uma restrição de
desigualdade do tipo
aj1 x1 + aj2 x2 + · · · + ajn xn ≤ bj .
A restrição de desigualdade pode ser substituı́da por uma restrição de igualdade introduzindo-se uma variável adicional xn+1 , não-negativa, conhecida como
variável de folga:
aj1 x1 + aj2 x2 + · · · + ajn xn + xn+1 = bj .
Do mesmo modo, introduz-se tantas variáveis de folga quantas forem as restrições do tipo ”≤” presentes no modelo original. O novo conjunto de variáveis será
formado pelas variáveis de decisão originais mais as eventuais variáveis de excesso
e de folga.
Variáveis livres
Pode ocorrer da formulação original do problema apresentar uma ou mais
variáveis de decisão irrestritas ou livres, isto é, sem sinal definido. Entretanto, a
forma padrão exige variáveis não–negativas. Essa dificuldade pode ser contornada
reescrevendo-se cada variável livre xj como a diferênça de duas outras variáveis
não-negativas, xj1 e xj2 , ou seja
xj = xj1 − xj2 .
A idéia é que qualquer quantidade (positiva, nula ou negativa) pode ser representada como a diferênça de duas quantidades não-negativas. Faz-se então a
substituição de cada variável livre por uma diferênça de variáveis não-negativas e
incorpora-se as novas variáveis à lista de variáveis de decisão do problema.
Não-negatividade dos bj ’s
Por razões a serem detalhadas oportunamente, exige-se que as constantes b j ,
j = 1, 2, . . . , m nos lados direitos das restrições do problema (2.2) sejam todas nãonegativas. Esta exigência pode ser atendidad multiplicando-se por −1 ambos os
lados de todas restrições tais que bj < 0. O resultado são novas restrições com lados
direitos positivos.
Problemas de maximização
Certos problemas de programação linear envolvem maximizar funções–objetivos, como a receita de uma empresa. O objetivo do problema se expressaria como
maximizar z(x) = p1 x1 + p2 x2 + · · · + pn xn ,
sujeito às restrições.
(2.3)
2.5. Exemplos ilustrativos
15
Assuma que x? = (x?1 , x?2 , . . . , x?n ) é uma solução ótima para o problema (2.3).
Da otimalidade de x? conclui-se que
z(x? ) ≥ z(x)
para toda solução viável x. Neste caso,
−z(x? ) ≤ −z(x)
e x? é também uma solução ótima para o problema de minimizar −z(x) sujeito
às mesmas restrições. Portanto, a substituição de maximizar por minimizar, seguida da troca dos sinais dos coeficientes da função–objetivo, fornece problemas
equivalentes do ponto de vista das variáveis de decisão. Os valores absolutos das
funções–objetivos serão iguais, porém com sinais trocados.
Constante na função–objetivo
A soma de uma constante qualquer a uma função objetivo não altera o problema do ponto de vista das variáveis de decisão. De fato, se x? é uma solução
ótima para o problema de minimizar
z(x) = c1 x1 + c2 x2 + · · · + cn xn ,
sujeito às restrições, então x? também é uma solução ótima para o problema de
minimizar z(x) + c0 , sendo c0 uma constante qualquer, uma vez que
z(x? ) + c0 ≤ z(x) + c0
para toda solução viável x. Constantes em funções–objetivos geralmente surgem da
consideração de custos fixos ou de reformulações visando formas padrões. Podem
ser desconsideradas para a obtenção de soluções ótimas e então somadas aos valores
ótimos das funções–objetivos.
2.5
Exemplos ilustrativos
Embora seja possı́vel colocar qualquer problema de programação linear na
forma padrão (2.2), não existe um procedimento sistemático para obter o modelo de
otimização básico do problema. Uso criterioso das hipóteses e treinamento exaustivo
são essenciais para se ganhar habilidade em modelagem de problemas de produção.
Exemplo 2.2 Uma joalheria produz dois diferentes tipos de estojos de madeira
para jogos de xadrez. O primeiro, menor, requer 3 horas de trabalho de torneamento; o segundo, maior, requer 2 horas. A empresa possui 4 tornos operados por
trabalhadores treinados, os quais trabalham, cada, 40 horas por semana. O estojo
menor demanda 1 kg de madeira; o maior demanda 3 kg. A empresa pode obter no
máximo 200 kg de madeira por semana. Os lucros unitários da empresa são de $20 e
$5 por unidade de estojo maior e menor, respectivamente. Deseja-se prescrever um
16
Capı́tulo 2. Programação Linear
programa de produção que vise maximizar o lucro total da empresa com a venda
dos estojos.
Sejam x1 e x2 as quantidades (não–negativas) de estojos de menor e maior
dimensões, respectivamente, produzidas durante uma semana. Para obter uma
restrição sobre horas trabalhadas, observa-se que a empresa possui 4 operadores
que trabalham, cada, 40 horas por semana nos tornos. Portanto, a empresa dispõe
de 160 horas de torneamento por semana. Dadas as diferentes quantidades de horas
necessárias para tornear os estojos, obtém-se a restrição de capacidade
3x1 + 2x2 ≤ 160.
A segunda restrição de capacidade, envolvendo as quantidades de madeira
utilizadas por unidade de estojos e a disponibilidade semanal de madeira para
produção, é dada por
x1 + 3x2 ≤ 200.
O modelo de otimização para a empresa então seria
maximizar z = 5x1 + 20x2
sujeito a
3x1 + 2x2 ≤ 160,
x1 + 3x2 ≤ 200,
com x1 ≥ 0 e x2 ≥ 0. Para obter a forma padrão do problema, introduz-se duas
variáveis de folga adicionais, x3 e x4 , transforma-se maximizar em minimizar e
trocam-se os sinais dos coeficientes da função–objetivo. O problema resultante será
minimizar −z = −5x1 − 20x2
sujeito a
3x1 +
2x2 + x3
= 160,
x1 +
3x2
+ x4 = 200,
com x1 ≥ 0, x2 ≥ 0, x3 ≥ 0 e x4 ≥ 0.
As hipóteses de proporcionalidade, aditividade e divisibilidade, implı́citas na
descrição textual do problema, tornaram mais simples sua formulação matemática.
Na prática, um operador de torno provavelmente levaria mais tempo para tornear
as primeiras unidades de estojos dos que as subseqüentes. Com a hipótese de proporcionalidade, assume-se tempos iguais para todas as unidades de um mesmo tipo.
Além disto, não são considerados os tempos necessários para ajustes dos tornos
(desligamento, limpeza, instalação de novas ferramentas, religamento) quando estes passam a tornear estojos de tipos diferentes. Com a hipótese da aditividade,
assume-se que os tempos de ajustes podem ser desprezados, e os tempos de torneamento efetivos, simplesmente somados. Finalmente, como se trata da produção
semanal da empresa e não existem prazos para entrega de estojos, estojos nãoacabados numa semana podem ser acabados na semana seguinte, o que valida a
hipótese de divisibilidade.
2
Exemplo 2.3 Um fazendeiro utiliza no mı́nimo 400 kg de ração especial por dia.
A ração é uma mistura de milho e soja com as composições indicadas na tabela 2.1.
2.5. Exemplos ilustrativos
17
Tabela 2.1: Dados do problema de dieta.
kg/kg de alimento
Alimento Proteı́na
Fibra
Custo ($/kg)
Milho
0.09
0.02
0.60
Soja
0.60
0.06
1.80
Um mı́nimo de 30% e um máximo de 5% da quantidade total de alimento
consumida por dia são estabelecidos para as quantidades totais de proteı́na e fibra
presentes na dieta. O fazendeiro deseja determinar a mistura de milho e soja que
produz uma dieta diária de mı́nimo custo.
Sejam x1 e x2 as quantidades (não–negativas) em kg de milho e soja na dieta
diária procurada pelo fazendeiro. Como no mı́nimo 400 kg de ração são utilizados,
x1 + x2 ≥ 400.
A prescrição para consumo de proteı́nas implica numa restrição do tipo
0.09x1 + 0.60x2 ≥ 0.30(x1 + x2 ),
ou ainda
0.21x1 − 0.30x2 ≤ 0.
Do mesmo modo, para fibra,
0.02x1 + 0.06x2 ≤ 0.05(x1 + x2 ),
ou seja,
0.03x1 − 0.01x2 ≥ 0.
O modelo linear de otimização para a
minimizar z = 0.60x1
sujeito a
0.21x1
0.03x1
x1
dieta diária seria
+ 1.80x2
− 0.30x2
− 0.01x2
+
x2
≤
≥
≥
0,
0,
400,
com x1 ≥ 0 e x2 ≥ 0. A forma padrão do problema é obtida introduzindo-se uma
variável de folga na primeira restrição e variáveis de excesso na segunda e terceira
restrições.
2
Exemplo 2.4 Um restaurante fast–food vende dois tipos de sanduı́ches. Os sanduı́ches utilizam 120 g e 90 g de carne, respectivamente. O restaurante abre as
portas com 90 kg de carne em estoque, mas pode comprar mais carne a $0.50/kg,
preço que inclui o custo de entrega. Qualquer excesso de carne no final do dia é
doado para uma instituição de caridade. Os lucros do restaurante com os sanduı́ches
são de $0.20 e $0.15 por unidade, respectivamente; o restaurante não espera vender
mais do que 900 sandı́ches por dia. Quantos sanduı́ches de cada tipo o restaurante
deveria produzir para maximizar seu lucro diário?
18
Capı́tulo 2. Programação Linear
Sejam x1 e x2 as quantidades (não–negativas) de sanduı́ches dos tipos 1 e 2 a
serem produzidas. Se o restaurante se mantiver dentro do limite de 90 kg de carne
por dia, então
0.12x1 + 0.09x2 ≤ 90.
Porém, o restaurante pode adquirir mais carne, e, neste caso,
0.12x1 + 0.09x2 ≥ 90.
A princı́pio, não se sabe qual das alternativas será mais vantajosa para o restaurante: operar com folga ou excesso de carne. Uma solução é introduzir uma
variável adicional x3 , livre, representando quantidade de carne, e escrever a restrição sobre utilização de carne como
0.12x1 + 0.09x2 + x3 = 90.
A variável x3 pode ser representada como a diferênça de variáveis não–negativas:
x3 = x31 − x32 . A restrição é então reescrita como
0.12x1 + 0.09x2 + x31 − x32 = 90.
Se x3 ≥ 0, o restaurante opera com folga de carne e o lucro total será
0.20x1 + 0.15x2 . Por outro lado, se x3 < 0, o restaurante incorrerá num custo adicional por comprar carne. Por motivos que serão detalhados quando da discussão
do método Simplex, as variáveis x31 e x32 não poderão assumir valores positivos
simultâneamente. Neste caso, se x3 < 0, então x31 = 0 e x32 > 0, de tal forma que
o lucro total do restaurante pode ser escrito como
0.20x1 + 0.15x2 − 0.50x32 .
O modelo linear de otimização para o restaurante seria
maximizar z = 0.20x1 + 0.15x2
− 0.50x32
sujeito a
0.12x
+
0.09x
+
x
x32
1
2
31 −
x1 +
x2
=
≤
90,
900,
com x1 ≥ 0, x2 ≥ 0, x31 ≥ 0 e x32 ≥ 0. Para obter a forma padrão do problema,
deve-se introduzir uma variável de folga na última restrição, substituir maximizar
por minimizar, e trocar os sinais dos coeficientes da função–objetivo.
2
Exemplo 2.5 Um banco precisa formular uma polı́tica de empréstimos envolvendo
uma quantia máxima de $12 milhões. A tabela 2.2 apresenta os parâmetros utilizados nos diferentes tipos de empréstimos com os quais o banco opera.
Tabela 2.2: Parâmetros utilizados pelo banco.
Tipo de
Taxa
Probabilidade
Empréstimo de Juros
de default
Pessoal
0.140
0.10
Automotivo
0.130
0.07
Habitacional
0.120
0.03
Agrı́cola
0.125
0.05
Comercial
0.100
0.02
2.5. Exemplos ilustrativos
19
Probabilidade de default significa probabilidade de que o empréstimo não seja
recuperado, e que portanto também não renda juros. A concorrência com outras
instituições financeiras obriga o banco a alocar no mı́nimo 40% dos recursos para
empréstimos agrı́colas e comerciais. Para apoiar a indústria civil da região, os recursos alocados para empréstimos habitacionais devem corresponder a, no mı́nimo,
50% dos recursos alocados para empréstimos pessoais, automotivos e habitacionais.
A polı́tica de banco estabelece que razão entre o montante total de empréstimos
default e o total de empréstimos deve ser de 0.04. O objetivo do banco é distribuir
os recursos disponı́veis entre as diferentes formas de empréstimos de forma a obter
o maior lucro possı́vel, entendido como a diferênça entre a receita total decorrente
de juros e o montante total perdido por default.
As quantidades (não–negativas) abaixo representam os montantes (em milhões)
a serem empregados em cada tipo de empréstimo.
x1 :
x2 :
x3 :
x4 :
x5 :
pessoais;
automotivos;
habitacionais;
agrı́colas;
comerciais.
Como o máximo disponı́vel para empréstimos é $12 (em milhões),
x1 + x2 + x3 + x4 + x5 ≤ 12.
Empréstimos agrı́colas e comerciais devem representar no mı́nimo 40% do
máximo disponı́vel:
x4 + x5 ≥ 4.8.
Empréstimos habitacionais devem corresponder a no mı́nimo 50% dos empréstimos pessoais, automotivos e habitacionais:
x3 ≥ 0.50(x1 + x2 + x3 ),
ou seja,
0.50x1 + 0.50x2 − 0.50x3 ≤ 0.
A polı́tica da empresa quanto a empréstimos default pode ser expressa como
0.10x1 + 0.07x2 + 0.03x3 + 0.05x4 + 0.02x5
≤ 0.04.
x1 + x 2 + x 3 + x 4 + x 5
(2.4)
O numerador de (2.4) é quanto o banco espera perder com a alocação de
recursos. A desigualdade (2.4) é equivalente a
0.06x1 + 0.03x2 − 0.01x3 + 0.01x4 − 0.02x5 ≤ 0.
O lucro total do banco é dado por
z = 0.14(0.90x1 ) + 0.13(0.93x2 ) + 0.12(0.97x3 ) + 0.125(0.95x4 )
+ 0.10(0.98x5 ) − (0.10x1 + 0.07x2 + 0.03x3 + 0.05x4 + 0.02x5 )
(2.5)
20
Capı́tulo 2. Programação Linear
A primeira parcela do lado direito de (2.5) é quanto o banco espera receber
de juros sobre os empréstimos; a segunda parcela contabiliza a perda devida a
empréstimos default. A função–objetivo (2.5) pode ser simplificada para
z = 0.026x1 + 0.0509x2 + 0.0864x3 + 0.06875x4 + 0.078x5 .
O modelo linear de otimização para o problema do banco seria
maximizar z = 0.026x1 + 0.0509x2 + 0.0864x3 + 0.06875x4 + 0.078x5
sujeito a
0.06x1 + 0.03x2 − 0.01x3 + 0.01x4 − 0.02x5
0.50x1 + 0.50x2 − 0.50x3
x4 + x 5
x1 + x 2 + x 3 + x 4 + x 5
≤ 0,
≤ 0,
≥ 4.8,
≤ 12,
com x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0 e x5 ≥ 0. A forma padrão do problema é
facilmente obtida introduzindo-se variáveis de folga na primeira, segunda e quarta
restrições, uma variável de excesso na terceira restrição, alterando-se maximizar
para minimizar, e trocando-se os sinais dos coeficientes da função–objetivo.
2.
2.6
Modelos com variáveis inteiras
Alguns modelos importantes de planejamento exigem que parte ou todas as
variáveis de decisão sejam variáveis inteiras, isto é, variáveis que podem assumir
somente valores inteiros. Como caso especial, variáveis binárias assumem apenas
os valores inteiros 0 ou 1. Costuma-se referir a um modelo linear com variáveis
inteiras como um modelo de programação linear inteira, embora, rigorosamente
falando, um modelo deste tipo não seja mais linear. Um modelo de programação
linear inteira é puro se contém somente variáveis inteiras; misto, se parte das
variáveis assume valores inteiros e a parte complementar, reais.
Certos modelos de programação linear inteira podem ser abordados por meio
do método Simplex, na qual a hipótese de divisibilidade é adotada, e ainda assim
obter-se decisões ótimas inteiras. Além disso, quando o modelo linear exibe certas propriedades estruturais, é possı́vel obter soluções ótimas inteiras por meio de
métodos especializados de programação linear, discutidos no Capı́tulo 3 do curso.
No caso geral será necessário utilizar métodos especı́ficos para resolver problemas
de programação linear inteira. Alguns destes métodos, os mais simples e gerais, são
tratados no Capı́tulo 4 do curso.
A modelagem de problemas de planejamento que envolvam variáveis inteiras
será introduzida neste capı́tulo.
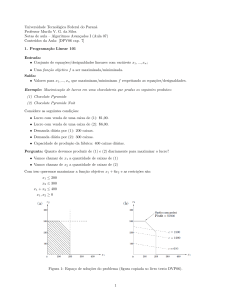
Exemplo 2.6 Uma empresa de planejamento de transportes urbanos está analisando a implantação de um novo sistema de transporte de massa por ônibus. Um
estudo inicial visa determinar a quantidade mı́nima de ônibus que devem ser colocados em operação para atender a demanda de passageiros. Após coletar informações,
o engenheiro de tráfego da empresa observou que o número mı́nimo de ônibus necessários para atender a demanda varia conforme a hora do dia, como ilustra a
figura 2.1, permanecendo constante a cada perı́odo de 4 horas, ou turnos. Cada
2.6. Modelos com variáveis inteiras
21
ônibus deve começar a circular no inı́cio de um dos turnos indicados e permanecer
circulando por 8 horas consecutivas. Deseja-se determinar a quantidade mı́nima de
ônibus em operação por dia que atenda a demanda de passageiros.
Uma primeira abordagem seria imaginar três perı́odos de oito horas (dois
turnos), de 8h às 16h, de 16h às 24h e de 24h às 8h, e definir x1 , x2 e x3 como os
números de ônibus começando o circular nos inı́cios destes perı́odos. O modelo de
otimização correspondente seria: minimizar
z = x1 + x2 + x3
sujeito a
x1 ≥ 10,
x2 ≥ 12
e x3 ≥ 8,
com x1 , x2 e x3 representando variáveis inteiras não-negativas. O número mı́nimo
de ônibus por dia seria 30. Entretanto, a abordagem adotada introduz uma restrição
que o problema original não possui, uma vez que os ônibus podem começar a circular
nos inı́cios de quaisquer turnos.
PSfrag replacements
No. de Ônibus
12
12
10
8
8
7
4
4
24
4
4
8
12
16
20
24 Hora do Dia
Figura 2.1: Demanda de ônibus por turnos.
Sejam então 1, 2, 3, 4, 5 e 6 ı́ndices indicativos dos turnos começando às 24h,
4h, 8h, 12h, 16h e 20h. Seja xi o número de ônibus que começam a circular no inı́cio
do turno i = 1, 2, 3, 4, 5, 6. Aos ônibus x1 que começam a circular às 24h somam-se
os ônibus que começam às 20h, e para atender a demanda do turno de 4 horas que
começa às 24h, deve-se impor que
x1 + x6 ≥ 4.
Procedendo da mesma maneira nos turnos subseqüentes de 4 horas, obtém-se
o seguinte modelo de otimização para o problema da empresa de transportes:
minimizar z = x1 + x2 + x3 + x4 + x5 + x6
sujeito a
x1 + x6 ≥ 4,
x1 + x2 ≥ 8,
x2 + x3 ≥ 10,
(2.6)
x
+
x
≥
7,
3
4
x4 + x5 ≥ 12,
x5 + x6 ≥ 4,
22
Capı́tulo 2. Programação Linear
com x1 , x2 , x3 , x4 , x5 e x6 variáveis inteiras não-negativas. (Observe que a forma
padrão da programação linear não se aplica a problemas com variáveis inteiras.) É
possı́vel mostrar que por meio do modelo (2.6), chega-se ao número mı́nimo de 26
ônibus em circulação por dia.
2
Exemplo 2.7 Cinco projetos estão sendo avaliados num horizonte de planejamento
de três anos. A tabela 2.3 fornece as receitas esperadas de cada projeto, juntamento
com o gasto previsto e o capital disponı́vel para investimento por ano. Os valores
encontram-se em $ milhões. Deseja-se determinar quais projetos devem ser executados no horizonte de 3 anos de forma obter a maior receita possı́vel.
O problema se resume a determinar se um projeto será ou não executado, o
que pode ser convenientemente representado por uma variável binária: para i =
1, 2, 3, 4, 5, define-se

 1, se o projeto i é executado,
xi =

0, caso contrário.
Tabela 2.3: Parâmetros dos cinco projetos.
Despesa Anual
Projeto 1
2
3
Receita
1
5
1
8
20
2
4
7
10
40
3
3
9
2
20
4
7
4
1
15
5
8
6
10
30
Capital 25 25
25
O modelo de programação linear inteira a ser utilizado para determinar que
projetos executar seria
maximizar z = 20x1 + 40x2 + 20x3 + 15x4 + 30x5
sujeito a
5x1 + 4x2 + 3x3 + 7x4 + 8x5 ≤ 25,
(2.7)
x1 + 7x2 + 9x3 + 4x4 + 6x5 ≤ 25,
8x1 + 10x2 + 2x3 + x4 + 10x5 ≤ 25,
com x1 , x2 , x3 , x4 e x5 variáveis binárias. É interessante notar que existem 25 = 32
maneiras de se atribuir valores iguais a 0 ou 1 para x1 , x2 , x3 , x4 e x5 , e assim obter
diferentes soluções para o problema. Um método simples, que funcionaria para o
modelo (2.7) seria:
1. Determine todas as possı́veis combinações de x1 , x2 , x3 , x4 e x5 :
{(0, 0, 0, 0, 0), (1, 0, 0, 0, 0), . . . , (1, 1, 1, 1, 1)};
2.6. Modelos com variáveis inteiras
23
2. Dentre as combinações obtidas, descarte as que não sejam viáveis, como por
exemplo, (1, 1, 1, 1, 1);
3. Dentre as combinações viáveis, obtenha uma – pode existir mais de uma –
que forneça o maior valor para z.
Este tipo de estratégia, chamada de solução por enumeração, é claramente
limitada a modelos que apresentem um pequeno número de variáveis binárias. 2
Exemplo 2.8 Três companhias telefônicas estão disputando sua preferência para
chamadas de longa distância. Os serviços oferecidos pelas companhias envolvem
um custo fixo mensal – assinatura – e um custo variável por minuto, resumidos na
tabela 2.4.
Tabela 2.4: Custos em $ por companhia.
Companhia Mensal Por Minuto
1
16
0.25
2
25
0.21
3
18
0.22
Você utiliza uma média de 200 minutos em chamadas de longa distância por
mês, não paga a assinatura da companhia caso não faça nenhuma chamada por meio
dela, e pode distribuir livremente suas chamadas entre as três companhias. Como
você deve utilizar os serviços das companhias de forma a minimizar o valor da sua
conta telefônica mensal?
O modelo para este problema envolve custos fixos e custos variáveis, que precisam ser refletidos nas variáveis de decisão. Sejam então x1 , x2 e x3 as quantidades
em minutos utilizadas com ligações por meio das companhias 1, 2 e 3. Defina
também, para i = 1, 2, 3,

 1, se xi > 0,
yi =

0, se xi = 0.
As variáveis binárias y1 , y2 e y3 indicam em que situação os custos fixos das
companhias devem ser levados em conta. Uma maneira de garantir que y i = 1 se
xi > 0 é definindo um número positivo M suficientemente grande e introduzindo a
desigualdade
xi ≤ M yi , i = 1, 2, 3.
Como x1 ≤ 200, i = 1, 2, 3, uma escolha conveniente é M = 200. (Valores
menores introduziriam restrições adicionais no modelo.) O modelo de otimização
que você deveria utilizar seria
minimizar z = 0.25x1 + 0.21x2 + 0.22x3 + 16y1 + 25y2 + 18y3
sujeito a
x1 + x2 + x3 = 200,
x1 ≤ 200y1 ,
(2.8)
x
≤
200y
,
2
2
x3 ≤ 200y3 ,
24
Capı́tulo 2. Programação Linear
com x1 , x2 e x3 , variáveis não-negativas, e y1 , y2 e y3 , variáveis binárias. O modelo de programação inteira (2.8) é misto, pois envolve variáveis reais e inteiras
(binárias). Existem 23 = 8 combinações de valores para y1 , y2 e y3 ; somente
(0, 0, 0) não é viável. Como para cada combinação viável (2.8) transforma-se num
modelo de programação linear, uma estratégia de solução seria: resolva os problemas de programação linear viáveis e determine a solução ótima que forneça o menor
valor. Como comentado anteriormente, estratégias de enumeração são limitadas a
problemas com poucas variáveis binárias.
2
Exemplo 2.9 O departamento responsável pela segurança de uma universidade
está discutindo a instalação de telefones públicos em localizações apropriadas do
campus. O departamento deseja instalar o menor número de telefones possı́vel,
mas de forma que cada uma das ruas principais seja atendida por no mı́nimo um
telefone. A figura 2.2 é um mapa com as principais ruas do campus, indicadas por
letras de A a K. Como o departamento deve alocar os telefones ?
Um telefone localizado em cruzamentos de ruas serve a no mı́nimo duas ruas.
Como existem 8 cruzamentos, numeradas de 1 a 8 na figura 2.2, no máximo 8 telefones serão necessários. É conveniente entãoPSfrag
definirreplacements
as seguintes variáveis binárias:
para i = 1, 2, . . . , 8,

 1, se um telefone é instalado no cruzamento i,
xi =

0, caso contrário.
1
2
A
3
B
K
I
G
F
H
E
6
5
C
4
J
D
7
8
Figura 2.2: Mapa do campus – principais ruas.
No mı́nimo um telefone deve atender cada uma das 11 ruas, identificadas por
A, B, . . . , K. Para atender a rua A, por exemplo, é possı́vel instalar um telefone
no cruzamento 1 ou no cruzamento 2. Uma maneira de indicar esta restrição é por
meio da desigualdade
x1 + x2 ≥ 1.
2.7. Solução gráfica de problemas lineares
25
Restrições similares são obtidas para cada uma das ruas do compus. O modelo
de programação linear inteira que o departamento de segurança do campus deve
resolver é
minimizar z = x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8
sujeito a
x1 + x2 ≥ 1, (A)
x2 + x3 ≥ 1, (B)
x
(C)
4 + x5 ≥ 1,
x
+
x
≥
1,
(D)
7
8
x
+
x
≥
1,
(E)
6
7
(2.9)
x
+
x
≥
1,
(F )
2
6
x1 + x6 ≥ 1, (G)
x
(H)
4 + x7 ≥ 1,
x
+
x
≥
1,
(I)
2
4
x
+
x
≥
1,
(J)
5
8
x3 + x5 ≥ 1, (K)
com x1 , i = 1, 2, . . . , 8, variáveis binárias. Problemas da forma (2.9) são chamados
de problemas de cobertura. Um problema geral de cobertura apresenta zeros ou
uns como coeficientes dos lados esquerdos das restrições, restrições do tipo ”≥ 1” ,
e eventualmente custos não unitários. No modelo (2.9) admite-se implicitamente
que os custos de instalação dos telefones são iguais.
2
2.7
Solução gráfica de problemas lineares
Problemas de programação linear com até duas variáveis de decisão podem ser
representados e resolvidos graficamente. Embora limitada, a representação gráfica
permite evidenciar propriedades e as diversas situações que podem ser encontradas ao se resolver problemas com um número maior de variáveis. Para efeito de
exposição, considere o seguinte problema de programação linear:
maximizar z = x1 + 2x2
sujeito a
x1 + x2 ≤ 8,
(2.10)
−x
+ 2x2 ≤ 4,
1
2x1 − x2 ≤ 12,
com x1 ≥ 0 e x2 ≥ 0.
Considere o plano x1 × x2 , com os eixos das abcissas e das ordenadas representando possı́veis valores para as variáveis de decisão x1 e x2 . Cada uma das
restrições descreve uma região do plano. Para obter a região associada à restrição
x1 + x2 ≤ 8, descreve-se inicialmente a reta x1 + x2 = 8, que passa pelos pontos
(0, 8) e (8, 0). A reta x1 + x2 = 8 divide o plano em dois semiplanos, x1 + x2 ≤ 8 e
x1 +x2 ≥ 8. A região x1 +x2 ≤ 8 corresponde ao semiplano que contém a origem do
plano, pois 0 + 0 ≤ 8. Repete-se o procedimento para todas as restrições presentes
no modelo. A interseção das regiões descritas pelos semiplanos representa a região
viável do problema, ilustrada na figura 2.3.
PSfrag replacements
26
Capı́tulo 2. Programação Linear
x2
8
x1 + x 2 = 8
−x1 + 2x2 = 4
6
4
24
2x1 − x2 = 12
c
z = 16
3
−4
0
1 2
4
6 20
8
z = 12
x1
3
z=8
z=4
z=0
z = −4
Figura 2.3: Representação gráfica do problema (2.10).
A região viável possui infinitos pontos e, em princı́pio, qualquer um deles pode
ser uma solução ótima do problema. Para determinar qual deles produz o maior
valor para z, usa-se o fato de que x1 +2x2 = z descreve uma famı́lia de retas paralelas
de inclinação −0.5 parametrizada pelo valor de z. Diferentes valores de z levam
a diferentes pontos de cruzamento com os eixos x1 e x2 . Retas correspondentes a
valores selecionados de z encontram-se representadas na figura 2.3. Para determinar
o sentido de crescimento de z, utiliza-se o conceito de gradiente de uma função
num ponto. O vetor gradiente de qualquer função diferenciável z = z(x) de n
variáveis num ponto x = (x1 , x2 , . . . , xn ), denotado por ∇z(x), é o vetor formado
pelas primeiras derivadas parciais da função no ponto considerado:
∂z(x) ∂z(x)
∂z(x)
∇z(x) =
.
,
, ... ,
∂x1
∂x2
∂xn
O vetor gradiente indica o sentido de maior crescimento da função no entorno
do ponto considerado. Observa-se que o vetor gradiente de uma função linear,
z = c 1 x1 + c 2 x2 + · · · + c n xn ,
é constante e dado por
c = (c1 , c2 , . . . , cn ).
No caso do exemplo ilustrativo, c = (1, 2). O sentido do gradiente está indicado
na figura 2.3. O vetor gradiente é ortogonal a qualquer reta que descreva um valor
para a função objetivo. Dois vetores x, y de n componentes são ortogonais se o seu
2.7. Solução gráfica de problemas lineares
27
produto escalar, definido por
x 1 y1 + x 2 y2 + · · · x n yn ,
é igual a zero. Sejam então x, y dois pontos quaisquer pertencentes à reta correspondente a um valor z = z0 para a função objetivo. Neste caso, x1 +2x2 = y1 +2y2 = z0 ,
e portanto
(x1 − y1 ) + 2(x2 − y2 ) = 0,
indicando que os vetores c e x − y, este último sobre a reta associada a z 0 , são
ortogonais.
A maximização do valor da função-objetivo no problema (2.10) pode ser conduzida da seguinte forma: percorre-se a região viável do problema no sentido do
gradiente (aumentando continuamente o valor da função-objetivo) até que a fronteira da região seja eventualmente atingida. O valor máximo da função-objetivo na
região viável é dado pelo valor da reta que toca a fronteira, no caso z ? = 12. Qualquer ponto pertencente à reta de valor z ? = 12 que também pertença à fronteira
é uma solução ótima do problema. No caso do exemplo ilustrativo (2.10), existe
apenas uma solução ótima, x? = (4, 4).
Se o objetivo do problema (2.10) fosse, ao invés de maximizar, minimizar
o valor de z, adotar-se-ia a direção contrária à do gradiente – aquela de maior
decrescimento da função. O valor mı́nimo da função-objetivo seria z ? = 0, obtido
no ponto x? = (0, 0). As análises de situações mais gerais, a seguir, aplicam-se
também a problemas de minimização.
Soluções ótimas únicas e múltiplas
A resolução gráfica do problema (2.10) conduz a uma solução ótima única.
Entretanto, é possı́vel que exista mais de uma solução ótima para um dado problema
de programação linear. Considere novamente o problema (2.10), mas suponha que
a função-objetivo foi alterada para
z = x1 + x2 .
O procedimento gráfico sugerido fará então com que a reta correspondente ao
maior valor de z toque a fronteira em múltiplos pontos sobre a reta x1 + x2 = 8.
O valor máximo da função-objetivo será z ? = 8 e qualquer ponto no segmento de
reta que liga os pontos (4, 4) e (20/3, 4/3) é uma solução ótima do problema.
Problemas ilimitados
Nos exemplos tratados até o momento foi possı́vel obter valores máximos limitados para a função-objetivo por meio de uma ou mais soluções ótimas. Existem
situações, quase sempre decorrentes de formulações inadequadas do problema, nas
quais não é possı́vel limitar superiormente o valor da função-objetivo. Suponha que
as restrições x1 + x2 ≤ 8 e 2x1 − x2 ≤ 12 do problema (2.10) são removidas, como
ilustra a figura 2.4. A região viável torna-se aberta na direção do gradiente, e
28
Capı́tulo 2. Programação Linear
PSfrag replacements
sempre será possı́vel obter um valor para a função objetivo maior do que o anterior.
Um problema linear com essa caracterı́stica é chamado de ilimitado. O valor de z
tende a +∞ e não é possı́vel caracterizar uma solução ótima para o problema.
x2
8
1
6
−x1 +x12x+2 x=2 4= 8
4
2
−4
0
2x1 − x2 = 12
c
z = 16
2
4
6
z = 12
x1
8
z = 8−4
20
z=4
3
4
3
z=0
Figura 2.4: Representação gráfica – problema ilimitado.
Problemas inviáveis
Diz-se que um problema de programação linear é viável se existe pelo menos
um ponto que satisfaz todas as restrições do problema, ou seja, se a região viável
do problema é não-vazia. Caso contrário, diz-se que o problema é inviável. Todos
os exemplos discutidos até agora referem-se a problemas viáveis. Entretanto, formulações inadequadas podem levar a problemas inviáveis. Considere, por exemplo,
o problema (2.10) com os sinais da segunda e terceira restrições lineares invertidos:
maximizar z = x1
sujeito a
x1
−x
1
2x1
+
+
+
−
2x2
x2
2x2
x2
≤
≥
≥
8,
4,
12,
(2.11)
com x1 ≥ 0 e x2 ≥ 0. Esta modificação é suficiente para tornar o problema (2.11)
inviável: a interseção dos semiplanos gerados pelas três restrições é vazia, como
ilustra a figura 2.5.
PSfrag replacements
2.8. Revisão de álgebra linear e matrizes
29
x2
8
x1 + x 2 = 8
−x1 + 2x2 = 4
6
4
24
2x1 − x2 = 12
c
z = 16
3
−4
0
1 2
4
6 20
8
z = 12
x1
3
z = 8−4
z=4
z=0
Figura 2.5: Representação gráfica – problema inviável.
Propriedade fundamental da programação linear
A interseção das restrições do problema (2.10) descreve um polı́gono, com
pontos extremos e arestas conhecidas. A região viável de um problema com
mais de duas variáveis seria descrita por um poliedro. Os cinco pontos extremos
da região viável do problema (2.10) são (0, 0), (0, 2), (4, 4), (20/3, 4/3), (6, 0). Cinco
arestas ligam estes pontos extremos.
A análise gráfica do problema (2.10) sugere que soluções ótimas podem ser
caracterizadas de duas formas: como um ponto extremo ou como um conjunto de
pontos sobre uma aresta da região viável. Mas, mesmo neste último caso, pelo menos
uma solução ótima é um ponto extremo da região viável. Esta conclusão pode ser
generalizada: se um problema de programação linear qualquer tiver soluções viáveis
ótimas, uma delas será um ponto extremo da região viável. Assim, embora a região
viável do problema geralmente contenha uma infinidade de pontos, para resolvêlo basta analisar um número finito de pontos extremos. Para resolver (2.10), por
exemplo, bastaria calcular z nos pontos extremos da região viável e declarar solução
ótima aquele que produzisse o maior valor. O método Simplex para programação
linear nada mais é do que uma busca orientada de soluções ótimas como pontos
extremos da região viável do problema considerado.
2.8
Revisão de álgebra linear e matrizes
Interpretações geométricas como as apresentadas na seção anterior são úteis,
mas naturalmente limitadas a problemas com duas ou três variáveis de decisão, no
máximo. Em dimensões maiores é necessário generalizar noções como as de ponto
30
Capı́tulo 2. Programação Linear
e reta, e adotar uma representação adequada para os problemas tratados. Nesta
seção são revistos os principais conceitos de álgebra linear e matrizes aplicáveis ao
estudo de programação linear.
Cada conjunto x = (x1 , x2 , . . . , xn ) de valores possı́veis para as variáveis de
decisão de um problema linear pode ser visto como um vetor do espaço linear R n ,
o que se denota como x ∈ Rn . As quantidades x1 , x2 , . . . , xn são as componentes
do vetor x. Dois vetores x, y ∈ Rn são iguais se xi = yi para todo i = 1, 2, . . . , n.
A soma de vetores e a multiplicação de um vetor por um escalar são definidas
no Rn como
x + y = (x1 + y1 , x2 + y2 , . . . , xn + yn ),
αx = (αx1 , αx2 , . . . , αxn ),
α ∈ R.
O vetor nulo do Rn é o vetor composto por n valores reais iguais a zero:
0 = (0, 0, . . . , 0).
A distinção entre o vetor nulo do Rn e o real zero será estabelecida pelo contexto. A notação xji será empregada para representar a i-ésima componente de um
vetor xj . Vetores podem ser representados graficamente associando-se as componentes do vetor a eixos cartesianos. O vetor nulo é representado na intersecção
dos eixos, denominada de origem, e um vetor qualquer, como um segmento orienPSfrag replacements
tado a partir da origem. A figura 2.6 ilustra as operações de soma e produto por
2
escalar no R .
x2 + y 2
x2
x
y2
0
αx
x+y
x
y
x1
y1 x 1 + y 1
(α > 1)
0
Figura 2.6: Operações básicas com vetores do R2 .
Combinação linear
Seja C = {x1 , x2 , . . . , xk } um conjunto qualquer de k vetores do Rn . Sejam
ainda α1 , α2 , . . . , αk escalares reais quaisquer. Uma expressão da forma
α1 x 1 + α 2 x 2 + · · · + α k x k
é chamada de combinação linear dos vetores de C, e resulta num vetor do R n .
Observe o emprego das operações de soma, dois-a-dois, e de multiplicação de vetores
por escalares, introduzidas anteriormente.
2.8. Revisão de álgebra linear e matrizes
31
Exemplo 2.10 Assuma k = 2, x1 = (1, 0, −1), x2 = (−4, 1, 2), α1 = 1 e α2 = −2.
Então
α1 x1 + α2 x2 = 1 · (1, 0, −1) + (−2) · (−4, 1, 2) = (−3, −2, −5).
2
.
Uma combinação linear de vetores pode ser representada graficamente deslocando-se α2 x2 para a extremidade de α1 x1 , e assim sucessivamente, até deslocar-se
αk xk para a de αk−1 xk−1 . A ligação da origem com a extremidade deslocada de
αk xk resulta no vetor gerado pela combinação linear.
Dependência linear
Seja C = {x1 , x2 , . . . , xk } um conjunto qualquer de k vetores do Rn . Diz-se
que C é linearmente dependente se existem escalares α1 , α2 , . . . , αk , não todos
nulos, tais que
k
X
αj xj = α1 x1 + α2 x2 + · · · + αk xk = 0.
(2.12)
j=1
Se a igualdade (2.12) for verdadeira somente se α1 = α2 = . . . = αk = 0,
diz-se então que C é linearmente independente.
Exemplo 2.11 Assuma k = 2, x1 = (1, 0, −1) e x2 = (−4, 1, 2). A partir de (2.12),
obtém-se
α1 x1 + α2 x2 = (α1 − 4α2 , α2 , −α1 + 2α2 ) = (0, 0, 0).
Da igualdade de vetores, chega-se ao sistema de equações
α1 − 4α2 = 0,
(2.13)
α2 = 0,
−α1 + 2α2 = 0.
(2.14)
(2.15)
Como a única solução possı́vel para o sistema (2.13)-(2.15) é α 1 = α2 = 0, o
conjunto C = {(1, 0, −1), (−4, 1, 2)} é linearmente independente.
2
Se um conjunto de vetores é linearmente independente, costuma-se dizer que
os vetores do conjunto são linearmente independentes.
Base e dimensão
Um conjunto C = {x1 , x2 , . . . , xk }, com xj ∈ Rn , j = 1, 2, . . . , k, é uma base
do R se C é linearmente independente e qualquer vetor do Rn pode ser escrito
como uma combinação linear dos vetores de C. Diz-se neste caso que o conjunto C
gera o Rn .
n
32
Capı́tulo 2. Programação Linear
Exemplo 2.12
(a) O conjunto C = {(1, 0, 0), (0, 1, 0} é linearmente independente, mas nem todos
os vetores do R3 podem ser escritos como combinações lineares dos vetores de C,
como por exemplo x = (0, 0, 1). Logo, C não é uma base do R3 ;
(b) O conjunto C = {1, 0), (0, 1), (1, 1)} não é linearmente independente, mas gera
o R2 . Dado um vetor qualquer x = (x1 , x2 ), basta definir os escalares α1 = x1 ,
α2 = x2 e α3 = 0 para obter x como combinação dos vetores de C:
x = x1 (1, 0) + x2 (0, 1) + 0(1, 1).
Entretanto, C não é uma base do R2 ;
(c) Os conjuntos C = {(1, 0, 0), (0, 1, 0), (0, 0, 1)} e C = {(1, 0), (0, 1)} são bases do
R3 e R2 , do mesmo modo que C = {(1, 0, 0), (1, 1, 0), (0, 1, 1)} e C = {(1, 1), (0, 1)}.
2
Seja C = {x1 , x2 , . . . , xk } uma base do Rn . Então para um dado x ∈ Rn
existem escalares α1 , α2 , . . . , αk tais que
x = α 1 x1 + α 2 x2 + · · · α n xk .
Os escalares α1 , α2 , . . . , αk são chamados de representação de x na base
C. A representação de um vetor varia conforme a base considerada, como ilustra a
figura 2.7.
β1 y 1
α1 x 1
PSfrag replacements
x
y1
x1
x2
0
α2 x 2
y 2 β2 y 2
Figura 2.7: Diferentes representações para um vetor do R2 .
É possı́vel mostrar que a representação de um vetor numa dada base é única,
e que todas as bases possuem exatamente o mesmo número de vetores. O conjunto
de n vetores
C = {(1, 0, . . . , 0), (0, 1, . . . , 0), . . . , (0, 0, . . . , 1)}
2.8. Revisão de álgebra linear e matrizes
33
é chamado de base canônica do Rn . É linearmente independente e qualquer vetor
pode ser escrito como combinação linear dos seus vetores. A representação de um
vetor qualquer x na base canônica é α1 = x1 , α2 = x2 , . . . , αn = xn , se confundindo
com o próprio vetor.
Uma vez que o número de vetores na base canônica é igual a n, e dado que
todas as bases devem conter o mesmo número de vetores, conclui-se que todas as
bases do Rn possuem n vetores. A dimensão de um espaço linear é igual ao número
de vetores nas suas bases. Portanto, a dimensão do Rn é igual a n.
Produto escalar e norma
O produto escalar de dois vetores x, y ∈ Rn é o escalar definido como
hx, yi = x1 y1 + x2 y2 + · · · + xn yn .
Dois vetores x, y ∈ Rn são ortogonais se hx, yi = 0. Um vetor x ∈ Rn é
ortogonal a um conjunto qualquer de vetores C = {x1 , x2 , . . . , xk } se hx, xj i = 0
para todo j = 1, 2, . . . , k.
A norma euclidiana de um vetor x ∈ Rn é o escalar definido por
kxk = x21 + x22 + · · · + x2n
1/2
.
O ângulo θ no intervalo [0, π] formado por dois vetores não-nulos x, y ∈ R n
pode ser definido como
hx, yi
.
cos θ =
kxk kyk
Conjuntos poliedrais
Seja c ∈ Rn e α ∈ R um vetor não-nulo e um escalar qualquer, respectivamente.
O conjunto dos pontos
H = {x ∈ Rn : c1 x1 + c2 x2 + · · · + cn xn = α}
é chamado de hiperplano. Hiperplanos assumem as formas conhecidas de retas e
planos no R2 e R3 , respectivamente. Cada hiperplano determina dois semi-espaços
no Rn :
H− = {x ∈ Rn : c1 x1 + c2 x2 + · · · + cn xn ≤ α}
e
H+ = {x ∈ Rn : c1 x1 + c2 x2 + · · · + cn xn ≥ α}.
A intersecção de um número finito de semi-espaços descreve um poliedro no
Rn . A figura 2.8 ilustra poliedros (polı́gonos) no R2 descritos por semi-espaços
(semiplanos). As regiões determinadas pelos subespaços estão indicadas por setas.
Um poliedro pode ser aberto (figura 2.8(a)) ou fechado (figura 2.8(b)), dependendo
dos semi-espaços considerados.
34
Capı́tulo 2. Programação Linear
Poliedros podem ser caracterizados por meio dos seus pontos extremos,
como x1 , x2 e x3 nas figuras 2.8(a) e 2.8(b), e direções extremas, como d1 e d2
na figura 2.8(a).
x2
PSfrag replacements
x3
x2
d2
y
x
x
1
d
x3
x
1
x1
y
(a)
(b)
Figura 2.8: Poliedros no R2 descritos por semi-espaços.
Poliedros são conjuntos convexos, no sentido de que se x e y são vetores
quaisquer contidos num poliedro, então o vetor
x = λx + (1 − λ)y,
λ ∈ [0, 1],
chamado de combinação convexa de x e y, também pertence ao poliedro, qualquer
que seja λ ∈ [0, 1]. As combinações convexas de dois vetores descrevem um segmento
de reta cujas extremidades são os vetores, como ilustra a figura 2.8.
Matrizes
Uma matriz é qualquer arranjo retangular de números. Se o retângulo possui
m linhas e n colunas, diz-se que a matriz tem dimensão m × n. O conjunto das
matrizes reais de dimensão m × n é denotado por Rm×n . Uma matriz A ∈ Rm×n
genérica seria


a11 a12 · · · a1n
 a21 a22 · · · a2n 


A= .
..  .
..
..
 ..
.
. 
.
am1
am2
···
amn
Uma matriz A ∈ Rm×n pode também ser denotada como A = {aij }. Duas
matrizes A, B ∈ Rm×n são iguais se aij = bij para todo i = 1, 2, . . . , m e todo
j = 1, 2, . . . , n. A matriz 0 ∈ Rm×n é a matriz composta apenas por elementos
nulos.
2.8. Revisão de álgebra linear e matrizes
35
Vetores
Casos especiais importantes são as matrizes linha e coluna, obtidas quando
m = 1 e n = 1, respectivamente. Vetores do Rn podem ser vistos como matrizes
x ∈ R1×n ou x ∈ Rm×1 . Neste curso, vetores são representados por matrizes-colunas
e referenciados na forma usual, x ∈ Rn .
Operações básicas
A soma (subtração) de matrizes A, B ∈ Rm×n é a matriz definida por
A ± B = {aij ± bij }.
A soma de matrizes é comutativa (A+B = B +A) e associativa ((A+B)+C =
A + (B + C)).
O produto de uma matriz A ∈ Rm×n por um escalar α ∈ R é a matriz
definida por
αA = {αaij }.
O produto de matriz por escalar é comutativo (αA = Aα), associativo ((αβ)A =
α(βA)) e distributivo ((α + β)A = αA + βA, α(A + B) = αA + αB.)
O produto de matrizes A ∈ Rm×n e B ∈ Rn×p , de dimensões compatı́veis,
é a matriz C ∈ Rm×p definida por
C = AB = {cik =
n
X
aij bjk }.
j=1
O produto de matrizes não é comutativo, isto é, AB 6= BA, em geral, mesmo
quando os dois produtos são possı́veis. O produto de matrizes é associativo ((AB)C =
A(BC)) e distributivo com relação a soma de matrizes (A(B + C) = AB + AC).
A transposta de uma matriz A ∈ Rm×n é a matriz de dimensão n × m
denotada como AT e definida por
AT = {aji }.
Inversa e determinante
Se m = n, diz-se que a matriz é quadrada ou de ordem n. A diagonal principal de uma matriz quadrada de ordem n é formada pelos elementos
a11 , a22 , . . . , ann . Diz-se que uma matriz quadrada é diagonal se os elementos fora
da diagonal são todos nulos. Uma matriz diagonal de ordem n importante é a
matriz identidade:


1 0 ··· 0
 0 1 ··· 0 


.
I= . . .
. . ... 

 .. ..
0
0
···
1
36
Capı́tulo 2. Programação Linear
Dada uma matriz A de ordem n, se existir uma matriz B, também de ordem
n, tal que
AB = BA = I,
então que B é a matriz inversa de A. Existindo, a inversa de A é única. É comum
representar a inversa de A como A−1 .
O menor ij de uma matriz quadrada A de ordem n é a submatriz denotada
por Aij obtida deletando-se a i-ésima linha e a j-ésima coluna de A. O determinante de A é o escalar representado como det A ou | A |, definido recursivamente
da seguinte forma: se n = 1, então
det A = a11 .
Se n = 2,
det A = a11 a22 − a21 a12 .
Se n > 2, seleciona-se qualquer linha i e então
det A = (−1)i+1 ai1 (det Ai1 ) + (−1)i+2 ai2 (det Ai2 )+
· · · + (−1)i+n ain (det Ain ).
(2.16)