Escoamento em uma curva:

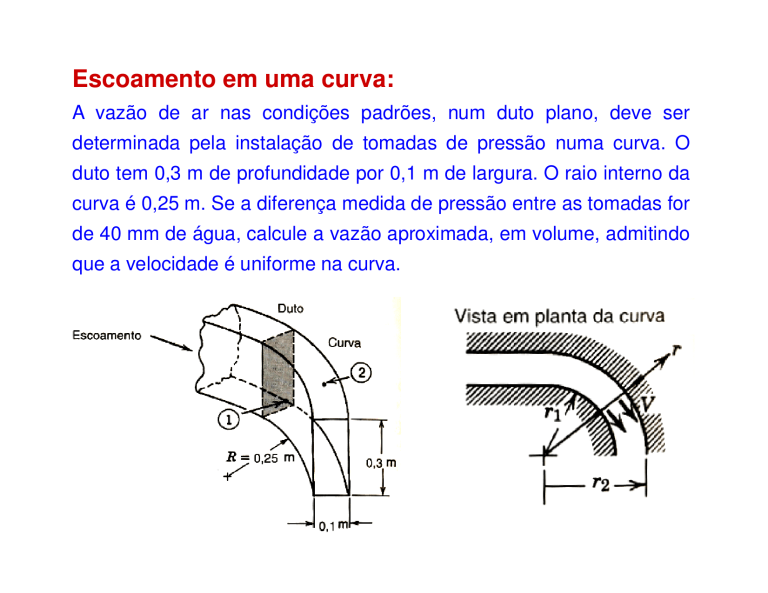
Escoamento em uma curva:
A vazão de ar nas condições padrões, num duto plano, deve ser
determinada pela instalação de tomadas de pressão numa curva. O
duto tem 0,3 m de profundidade por 0,1 m de largura. O raio interno da
curva é 0,25 m. Se a diferença medida de pressão entre as tomadas for
de 40 mm de água, calcule a vazão aproximada, em volume, admitindo
que a velocidade é uniforme na curva.
A Equação de Bernoulli – A integração da
Eq. de Euler ao longo d euma linha de
corrente
A analise de volume de controle diferencial,
conduziu a uma Eq. Diferencial, que quando
integrada, levou a uma forma da Eq. de Bernoulli. A
fim de dar um claro entendimento físico a respeito
das restrições aos resultados, uma dedução
adicional será apresentada.
Dedução com o emprego de coordenadas de linhas
de corrente
A Eq. de Euler para escoamento permanente ao longo de uma
linha de corrente é dada por:
Se uma partícula fluida mover-se de uma distancia, ds, ao longo
de uma linha de corrente, então:
Assim após multiplicar a Eq. anterior por ds, pode-se escrever:
Integrando esta equação:
Para o caso especial do escoamento incompressível, ρ =
constante, a Eq. anterior torna-se a Eq. de Bernoulli.
A Eq. de Bernoulli é um instrumento útil porque relaciona as
variações de pressão com as de velocidade e elevação ao longo
de uma linha de corrente. Ela dá resultados corretos apenas se
aplicada a uma situação de escoamento onde todas as 4
restrições são razoáveis.
Pressão estática de estagnação e dinâmica
A pressão p da Eq. de Bernoulli, é a pressão termodinâmica que
comumente é chamada de pressão estática e é bastante difícil de
medir numa situação pratica.
Foi demonstrado que não há variação de pressão numa direção
normal as linhas de corrente retilíneas. Isto torna possível medir a
pressão estática num fluido em movimento usando uma “tomada” de
pressão na parede do duto.
Se o orifício for perpendicular a parede do tubo e isento de rebarbas,
medições precisas da pressão estática poderão ser feitas pela sua
conexão a um medidor adequando.
A pressão estática pode ser medida também pelo emprego cuidadoso
de uma sonda de pressão. Esta deve ser projetada de modo que os
orifícios medidores sejam colocados corretamente com relação à
ponta e à haste da sonda. A seção medidora deve ser alinhada coma
direção do escoamento local.
As sondas de pressão encontram-se disponíveis no comercio em
tamanhos tão pequenos quanto 1,5 mm de diâmetro.
A pressão de estagnação é obtida quando um fluido em movimento
é desacelerado até velocidade zero por meio de um processo sem
atrito. No escoamento incompressível a Eq. de Bernoulli pode ser
usada para relacionar estas pressões, desprezando diferenças de
elevação.
Se a pressão estática for p, com velocidade V, a pressão de
estagnação p0 (onde a vel. de estagnação V0=0) seria:
A Eq. anterior é um anunciado matemático da definição de pressão de
estagnação valido para escoamento incompressível. O termo ½ ρV2 é
geralmente chamado de pressão dinâmica.
A pressão de estagnação é medida no laboratório usando-se uma
sonda com um orifício que fica voltado diretamente para a montante,
conforme mostrado na figura. Esse instrumento é chamado de sonda
de pressão ou tubo de Pitot. A seção de medição deve ficar alinhada
com a direção do escoamento local.
Duas possíveis configurações experimentais são mostradas:
As figuras mostram a medição simultânea das pressões estática e de
estagnação. O Tubo de Pitot estático também é conhecido como
Tubo Prandtl.
Tubo de Pitot
Um tubo de Pitot inserido
num
escoamento
de
ar
(Patm=715mmHg e T0=16°C)
a fim de medir a velocidade.
O tubo é introduzido de
forma
que
montante
aponta
e
a
para
pressão
sentida pela sonda é a de
estagnação.
A pressão estática é medida no mesmo ponto do escoamento pelo
emprego de uma tomada de pressão na parede. Se a diferença de
pressão é de 30 mm de Hg, determine a velocidade de escoamento.
P2
Livro texto:
- Introdução a Mecânica dos Fluidos – R. Fox
Cap 3: Escoamentos incompressíveis de fluidos não
viscosos.
- Introdução às ciências Térmicas - Schimidt, F.W.,
Cap 4. Escoamento interno e externo
- Mecânica dos Fluidos – Franco Brunetti
Resolução P1
1A. Responder verdadeiro (V) ou falso (F) nos seguintes enunciados: (10
ptos)
a) Quando o escoamento é tanto sem atrito como rotacional a equação da
quantidade de movimento se reduz a equação de Euler. (F)
b) Um escoamento de fluido inicialmente irrotacional pode se tornar rotacional
se existirem gradientes de entropia causados por ondas de choques curvas.(V)
c) A viscosidade cinemática resulta da relação da viscosidade dinâmica e o
volume específico. (F)
d) Eq. da viscosidade foi analisada por I. Newton que supôs uma película de
lubrificante entre duas laminas, umas das quais é fixa. (V)
e) Para o ar em condições padrões, um escoamento pode ser considerado
incompressível se a velocidade for menor que cerca de 100 km/h (F)
1B. Responder verdadeiro (V) ou falso (F) nos seguintes enunciados: (10
ptos)
a) È possível classificar os escoamentos como: permanente ou não
permanente, não viscoso ou viscoso, incompressível ou compressível,
gás ou liquido. (V)
b) Se considera fluxo hipersônico para um N°de Mach igual ou acima de 3. (F)
c) As abordagens básicas para as analise de problemas de escoamento
podem ser: de grande escala, de pequena escala e escala intermédia. (F)
d) A equação básica da quantidade de movimento, trata de uma equação
vetorial de 8 termos. (F)
e) A condição de irrotacionalidade é valida para um escoamento nas quais
as forças viscosas são desprezíveis. (V)
2A. Responder as seguintes perguntas (20 ptos)
Quais são as restrições da Equação de Bernoulli?
1. Escoamento permanente – uma hipótese comum, aplicável a muitos escoamentos.
2. Escoamento incompressível – aceitável, se o número de Mach do escoamento for
menor que 0,3.
3. Escoamento sem atrito – muito restritiva, as paredes solidas introduzem efeitos de
atrito.
4. Escoamento ao longo de uma linha de corrente – linhas de corrente diferentes podem
ter diferentes “ constantes de Bernoulli” w0 = p/ρ + V2/2 + gz, dependendo das
condições do escoamento.
5. Ausência de trabalho de eixo entre 1 e 2 – sem bombas ou turbinas sobre a linha de
corrente.
6. Ausência de troca de calor entre 1 e 2 – seja calor adicionado, seja calor removido.
2B. Responder as seguintes perguntas (20 ptos)
Explicar brevemente o fenômeno de cavitação em bombas hidráulicas.
CAVITAÇÃO
3A e B. Resolver o exercício. (20 ptos)
Se z é “para cima”, quais são as condições sobre as constantes a e b
para que o campo de velocidades u = ay, v = bx, w = 0 seja uma solução
exata das equações da continuidade e de Navier-Stokes para escoamento
incompressível?. O fluxo é irrotacional?.
4A. Resolver o exercício. (20 ptos)
Considere a turbina extraindo energia através de um conduto forçado em uma
barragem, como na figura. Para escoamento turbulento em dutos, a perda de
carga por atrito é aproximadamente hf = CQ2, onde a constante C depende das
dimensões do conduto forçado e das propriedades da água. Mostre que para uma
dada geometria de conduto forçado e vazão variável Q do rio, a máxima potencia
possível da turbina nesse caso é Pmax = 2ρgHQ/3 e ocorre quando a vazão é Q =
[H/(3C)]1/2.
4B. Resolver o exercício. (20 ptos)
A bomba da figura cria um jato de água a 20°C, orientado para atingir
uma distância horizontal máxima. As perdas por atrito do sistema são de 6,5
m. O jato pode ser aproximado pela trajetória de partículas sem atrito. Qual
potencia a bomba deve entregar?
5A e B Resolver o exercício. (30 ptos)
O acessório horizontal Y da figura, divide em partes iguais a vazão de
água a 20°C. Se Q1 = 142 l/s, P1 = 172,4 kPa (manométrica) e as perdas são
desprezadas, calcule (a) P2, (b) P3 e (c) o vetor força necessário para manter
o Y no lugar.