Document

GOIÂNIA, ____ / ____ / 2015
PROFESSOR: ROSIVANE
DISCIPLINA : MATÉMÁTICA
SÉRIE: 3º
ALUNO(a):____________________________
NOTA:
No Anhanguera você
é + Enem
LISTA DE MATEMÁTICA
1. ( UFCE ) Se f ( x ) = 161+1/x, então f ( -1 ) +
f ( -2 ) + f ( -4 ) é igual a :
a.
b.
c.
d.
e.
11
13
15
17
Nda
2. ( PUC - SP ) Se y = 10x é um número entre
1000 e 100 000, então x está entre:
a.
b.
c.
d.
e.
-1 e 0
2e3
3e5
5 e 10
10 e 100
a.
b.
c.
d.
e.
2
1
f(a)
f(1)
2f(a)
5. ( PUC - MG ) Os valores de a IR que tornam
a função exponencial f ( x ) = ( a - 3 )x decrescente
são :
a.
b.
c.
d.
e.
0<a<3
3<a<4
a<3ea 0
a>3ea 4
a<3
6. Resolva a equação exponencial:
3. ( PUC - MG ) Seja a função f ( x ) = ax . É
correto afirmar que :
a.
b.
c.
d.
e.
ela é crescente se x > 0
ela é crescente se a > 0
ela é crescente se a > 1
ela é decrescente se a 1
ela é decrescente se 0 < x < 1
4. ( PUC - RS ) Seja a função f: IR em IR
definida por f ( x ) = 2x . Então f ( a+1) - f (a) é
igual a:
11. (U. E. FEIRA DE SANTANA - BA) O gráfico
da função real f(x) = x2 - 2:
7. Resolva a equação exponencial:
a) intercepta o eixo dos x no ponto (1, 0);
b) intercepta o eixo dos x no ponto (0, 1);
c) intercepta o eixo dos x no ponto (2, 0);
d) intercepta o eixo dos x no ponto (0, -2);
e) não intercepta o eixo dos x.
8.
Resolva
a
equação
exponencial:
12. (FIC / FACEM) A produção de uma indústria
vem diminuindo ano a ano. Num certo ano, ela
produziu mil unidades de seu principal produto. A
partir daí, a produção anual passou a seguir a lei y
= 1000 . (0,9)x. O número de unidades produzidas
no segundo ano desse período recessivo foi de:
a)900
b)1000
c)180
d)810
e)90
9. (U. E. FEIRA DE SANTANA - BA)
O produto das soluções da equação (43 - x)2 - x = 1
é:
a) 0
b) 1
c) 4
d) 5
e) 6
10. As funções y = ax e y = bx com a > 0 e b > 0 e
a b têm gráficos que se interceptam em:
a) nenhum ponto;
b) 2 pontos;
c) 4 pontos;
d) 1 ponto;
e) infinitos pontos.
13. O valor de x na equação 251-x = 1/5 é:
a) 1/2
b) 3/2
c) 5/2
d) 7/2
e) -1/2
14. O número de pontos em comum dos gráficos
das funções f e g, ambas de domínio real sendo
f(x) = 2 x e g(x) = 3 x é:
a)
b)
c)
d)
e)
0
1
2
3
4
15. Resolva a equação 8 x = 0,25.
16.
8
Descubra
2
x −x
=4
x +1
o
valor
de
x
na
equação
.
A função exponencial expressa um crescimento
ou um decrescimento característico de alguns
fenômenos da natureza, bem como o
funcionamento dos juros compostos, importantes
na matemática financeira.
Vamos explorar um pouco algumas dessas
aplicações.
Geralmente, o crescimento de determinados seres
vivos microscópicos, como as bactérias, acontece
exponencialmente. Dessa forma, é comum o uso
de funções exponenciais relacionado a problemas
dessa natureza.
17. Calcule o valor de x na equação abaixo:
3
x −1
−3 +3
x
x +1
+3
x+2
= 306
18. Classifique os gráficos abaixo em crescente e
decrescente:
19. (PUC/MG - adaptada) - O número de
bactérias em um meio duplica de hora em hora.
Se, inicialmente, existem 8 bactérias no meio, ao
fim de 10 horas o número de bactérias será:
20. (UNISA) - Sob certas condições, o número de
bactérias B de uma cultura, em função do tempo t,
medido em horas, é dado por
. Isso
significa que 5 dias após a hora zero o número de
bactérias
é:
A
decomposição
ou
desintegração
de
determinadas substâncias também acontece
segundo um padrão exponencial. A chamada meia
vida de uma substância é o tempo necessário para
que ela reduza a sua massa pela metade. Eis aqui
outro caso de aplicação das funções exponenciais.
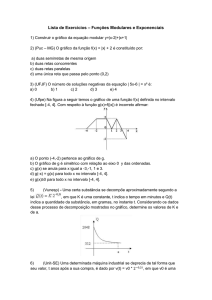
21. (Vunesp) - Uma certa substância se decompõe
23.
Resolva
a
equação
aproximadamente segundo a lei
,
em que K é uma constante, t indica o tempo em
minutos e Q(t) indica a quantidade da substância,
em gramas, no instante t. Considerando os dados
desse processo de decomposição mostrados no
gráfico, determine os valores de K e de a.
24. Resolva as equações exponenciais:
22. O sistema de juros compostos também
funciona
de
forma
exponencial.
O montante M é a quantia a ser recebida após a
aplicação de um capital C, a uma taxa i, durante
certo tempo t. No regime de juros compostos, esse
montante é calculado pela relação
.
Considere um capital de R$ 10.000 aplicado a
uma taxa de 12% ao ano durante 4 anos. Qual
seria o montante ao final dessa aplicação?
b) y = 3 – x
25. Construa o gráfico das funções:
a) y = 5 x