1. Levante as curvas completas de tensão versus deformação de

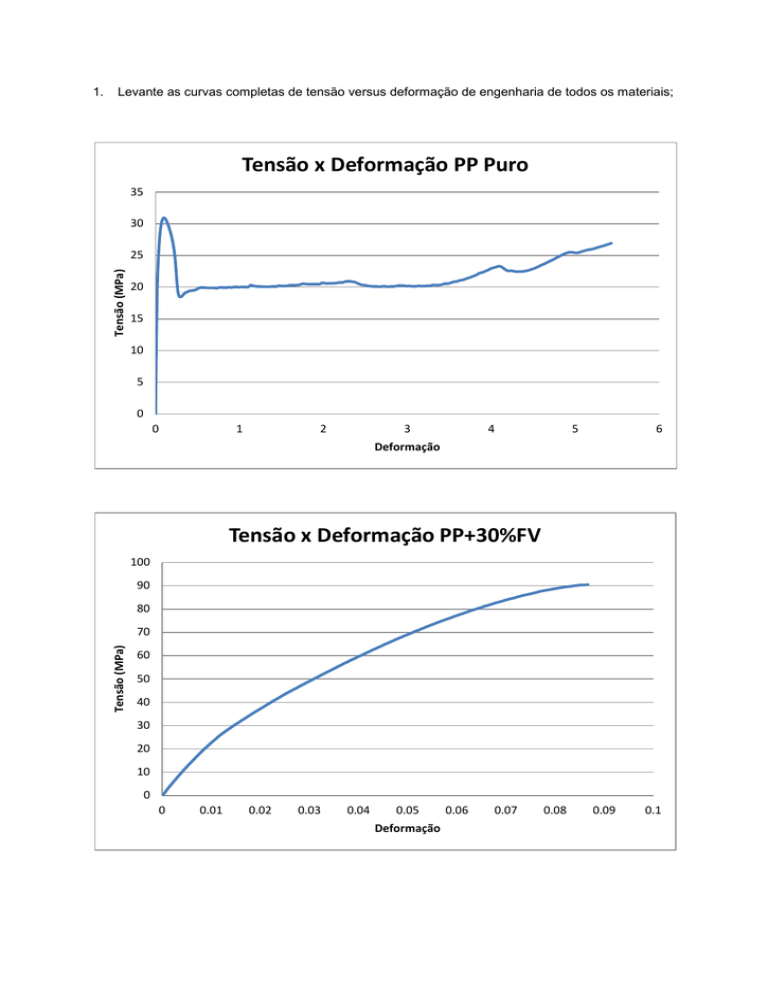
Levante as curvas completas de tensão versus deformação de engenharia de todos os materiais;
Tensão x Deformação PP Puro
35
30
Tensão (MPa)
25
20
15
10
5
0
0
1
2
3
4
5
6
Deformação
Tensão x Deformação PP+30%FV
100
90
80
70
Tensão (MPa)
1.
60
50
40
30
20
10
0
0
0.01
0.02
0.03
0.04
0.05
Deformação
0.06
0.07
0.08
0.09
0.1
2. Determine o módulo de elasticidade, os limites de escoamento e de resistência à tração e a
tensão de fratura dos materiais (propriedades nominais ou de engenharia), indicando as expressões
utilizadas nos cálculos;
Para determinação dos módulos de elasticidade, foram utilizados, conforme exemplificado na
planilha de dados, os dados de tensão e deformação até uma abertura de 7 mm do extensômetro.
Estes valores foram então ajustados, por regressão linear, a uma reta do tipo y = E.x, onde E é o
valor do módulo de elasticidade.
No polipropileno homopolímero puro, o limite de escoamento é determinado como o máximo
local à esquerda no gráfico. O limite de resistência à tração seria o máximo à direita, e coincidiria
com a tensão de fratura, porém, como não houve fratura deste cdp, não foi possível obter esses
valores.
E = 1256,613 MPa
Le = 30,9514 MPa
O material reforçado com fibras curtas de vidro apresenta comportamento frágil, e a fratura
ocorre ainda no regime elástico, portanto não há limite de escoamento e a tensão de fratura coincide
com o limite de resistência à tração.
E = 2263,117 MPa
Lt = 90,4801 MPa
3. Se possível, determine o alongamento e a estricção na fratura dos materiais, indicando as
expressões utilizadas nos cálculos. Note que, para isso, é fundamental a mensuração precisa do
comprimento e da seção transversal finais dos espécimes rompidos;
O alongamento de um corpo em ensaio de tração é dado por
por
𝐸=
𝐴𝑓 −𝐴0
𝐴0
𝐴=
𝐿𝑓 −𝐿0
𝐿0
e, a estricção,
. Nesta prática, não foi possível obter a estricção de nenhum dos corpos de prova
e, como não houve fratura do corpo não reforçado, é possível apenas dizer que seu alongamento
final seria maior que 543%. No corpo reforçado, o alongamento é de apenas 8,67%.
4. Numa base de massas ou densidades, compare os resultados de resistência mecânica destes
materiais com os de uma liga de alumínio de grau aeronáutico; 160 438
Comparando apenas termos de resistência, as ligas de alumínio de grau aeronáutico são
claramente melhores que os materiais poliméricos. Uma liga 2524-0 possui limite de resistência à
tração por volta de 160 MPa e, se utilizado o tratamento térmico T3, até 440 MPa, valor quase 5
vezes superior ao limite do polipropileno homopolímero reforçado com fibras de vidro.
Na indústria aeronáutica, porém, a economia de peso é importantíssima, e nem todos os
componentes do avião precisam suportar cargas tão extremas. A densidade de uma liga de alumínio
2024 é de 2,73 g/cm³, enquanto a do propileno cristalino é de 0,946 g/cm 3. Em termos de carga
suportada por densidade, o alumínio permanece superior, mas em aplicações de menor exigência, a
densidade pode se tornar o fator decisivo, o que explica o uso de polímeros em diversas aplicações
na indústria aeronáutica.
5. Explique os motivos das diferenças de comportamento mecânico dos materiais avaliados, em
termos da magnitude e do formato das curvas determinadas, bem como das propriedades
calculadas;
6. Compare e explique as diferenças entre os aspectos morfológicos das regiões de fratura dos
materiais ensaiados;
7. Confronte o formato das curvas tensão versus deformação dos materiais ensaiados ao de uma
liga de alumínio, ou de um aço. Explique as semelhanças e as diferenças entre elas; discuta os
resultados à luz da natureza dos materiais ensaiados, ou seja, polímeros puros, ou reforçados versus
metais;
8. Compare, dentre os materiais poliméricos ensaiados, os níveis de alongamento na fratura, e
depois os confronte-os àqueles obtidos nos ensaios de materiais metálicos. Discuta os resultados à
luz da natureza dos materiais ensaiados.